首页理论教育平面力系合成与平衡的方法分析

平面力系合成与平衡的方法分析

2023-06-26 理论教育版权反馈

【摘要】：平面汇交力系合成的几何法设一刚体受到平面汇交力系F1、F2、F3、F4 的作用，各力的作用线汇交于一点A。若平面汇交力系有n 个力，用FR 表示合力矢，则有合力矢对刚体的作用与原力系对该刚体的作用是等效的。图3-17几何法求约束力根据平面汇交力系平衡的几何条件，此3 个力可以组成一个封闭的三角形。

1.几何法

平面汇交力系是指，各力的作用线都在同一个平面内且汇交于一点的力系，这是最简单的力系。

（1）平面汇交力系合成的几何法

设一刚体受到平面汇交力系F1、F2、F3、F4 的作用，各力的作用线汇交于一点A。根据刚体内部力的可传性，可将各力的作用点沿其作用线移至汇交点A，如图3－16（a）所示，然后利用力的三角__形法则将各力依次合成，即从任选点a 作出矢量F1，在其末端b 作出矢量F2，则虚线（FR1）为力F1 与F2 的合力矢。依次作出F3、F4，则各分力组成了一个不封边的力多边形abcde，终点为e 点，即为4 个力的合力矢FR，如图3－16（b）所示。

pagenumber_ebook=124,pagenumber_book=119

图3-16　平面汇交力系的力多边形法则

各力矢与合力矢构成的多边形为力多边形，表示合力矢的边ae 称为力多边形的封闭边，用力多边形求合力FR 的几何作图规则称为力的多边形法则，这种方法又称为几何法。

根据矢量相加的交换律，任意变换各分力的作图顺序，可得形状不同的力多边形，但其合力FR 始终不变，如图3－16（c）所示。

使用力的多边形法则时应注意：

1）合力FR 为力的多边形的封闭边；

2）合力FR 的大小与相加次序无关；

3）合力FR 的作用点为首力的始点；

4）合力FR 的方向是从首力的始端指向末力的终端。

若平面汇交力系有n 个力，用FR 表示合力矢，则有

合力矢对刚体的作用与原力系对该刚体的作用是等效的。

（2）平面汇交力系平衡的几何条件

平面汇交力系几何法平衡的必要与充分条件是：该力系的合力为零，或力系中各力矢构成的力多边形自行封闭，即

用图解法求解平面汇交力系的平衡问题时，首先选取适当的比例画出封闭的力多边形，然后量得所要求的未知量。

【例3-3】　如图3－17（a）所示，支架的横梁AB 与斜杆DC 以铰链C 相连接，C 点为AB 杆的中点，铰链A、D 以铰链与铅直的墙连接，杆DC 与水平面成45°；载荷F＝10 kN。设梁和杆的重量忽略不计，求铰链A 的约束力和杆DC 所受的力。

解：选取横梁AB 为研究对象。横梁AB 在B 处受载荷F 的作用。杆DC 为二力杆，所以在C 点对横梁的作用力为FC，如图3－17（b）所示。铰链A 点的约束力的作用线可根据三力平衡汇交定理确定，即通过另外两个力的交点E。

pagenumber_ebook=125,pagenumber_book=120

图3-17　几何法求约束力

根据平面汇交力系平衡的几何条件，此3 个力可以组成一个封闭的三角形。按照图中的比例尺先画出力F，再根据FC 和FA 的方向组成封闭的三角形，即可量出FA 的大小。如图3－17（b）和图3－17（c）所示，求得

根据作用力与反作用力，作用在杆DC 的C 端的力F′C 与FC 大小相等、方向相反，可见DC 杆受压力，如图3－17（b）所示。

封闭三角形也可以按图3－17（d）所示来求得FC 和FA，结果是相同的。

2.解析法

（1）平面汇交力系合成的解析法

由于受到作图精度的限制，几何法求力系合力往往不能满足工程要求。因此，工程上常采用解析法解决实际问题。

设力F 作用于一个刚体上，如图3－18（a）所示，建立直角坐标系式xOy，则F在x，y 轴上的投影为

pagenumber_ebook=126,pagenumber_book=121

图3-18　力在x，y 轴上的投影

设由n 个力组成平面汇交力系作用于一个刚体上，如图3－18（b）所示，将各力分别向x，y 轴投影，根据合力矢投影定理：合力矢在某一轴上的投影等于各分力矢在同一轴上投影的代数和，可得

式（3－4）中，FRx，FRy 为合力在x，y 轴上的投影；Fx1 和Fy1，Fx2 和Fy2，…，Fxn和Fyn分别为各分力在向x 和y 轴上的投影。

由图3－18（c）可得合力矢的大小和方向为

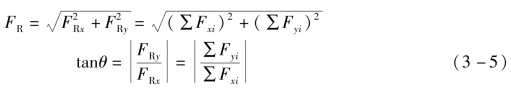
pagenumber_ebook=126,pagenumber_book=121

【例3-4】　如图3－19 所示，已知力F1＝500 N，F2＝300 N，F3＝600 N，F4＝1 000 N，作用于O 点，各力方向如图3－19 所示，求它们的合力大小和方向，并在图中画出。

解：由式（3－4），可得

pagenumber_ebook=126,pagenumber_book=121

由式（3－5），可得

合力FR 与x 轴的夹角为

pagenumber_ebook=126,pagenumber_book=121

pagenumber_ebook=126,pagenumber_book=121

图3-19　受力示意图

（2）平面汇交力系平衡的解析条件和平衡方程

由于平面汇交力系平衡的充分必要条件是该力系的矢量和为零，因此力系中各力在x，y 轴上的投影的和必须等于零，故平面汇交力系平衡的充分必要条件是

式（3－6）是平面汇交力系的平衡方程，它以解析形式表示汇交力系平衡的充分必要条件：力系中各力在力系平面内x，y 轴上的投影的代数和分别等于零。由两个独立的方程，可以求解两个未知量。

【例3-5】　如图3－20（a）所示，支架由杆AB、BC 构成，A，B，C 三点处均为铰链连接。在A 点悬挂重量G＝10 kN 的重物，求杆AB、AC 所受的力，杆的自重不计。

pagenumber_ebook=127,pagenumber_book=122

图3-20　AB、BC 杆受力示意图

解：（1）确定研究对象。取A 处铰接点为研究对象。

（2）画出受力图，如图3－20（b）所示。

（3）建立坐标系：

由∑Fx＝0，－FAC－Gcos60°＝0，得FAC＝－Gcos60°≈－5 kN；

由∑Fy＝0，FAB－Gsin60°＝0，得FAB＝Gsin60°≈8.7 kN。

由计算结果可知，FAC为负值，表示该力实际指向与受力图中假设的指向相反，说明杆件AC 受压；FAB为正值，表示该力实际指向与受力图中假设的指向相同，说明杆件AB 受拉。