平面力系合成的解析法及平衡条件

2025-09-29 理论教育版权反馈

【摘要】：若已知Fx、Fy 值，可求出F 的大小和方向，即2.平面汇交力系合成的解析法设刚体上作用有一个平面汇交力系F1、F2、…应用式（3-6）、式（3-7）计算合力大小和方向的方法，称为平面汇交力系合成的解析法。案例3-4 求图3-12 所示平面汇交力系的合力。式（3-9）称为平面汇交力系的平衡方程，这是相互独立的两个方程，所以只能求解两个未知量。由于滑轮的大小可忽略不计，故这些力可看作是平面汇交力系。

1.力在直角坐标轴上的投影

设力F 作用在刚体上的A 点，建立直角坐标系Oxy，使它与力F 的作用线在同一平面内，如图3-11 所示。从力F 的起点A 和终止点B 分别向x 轴和y 轴作垂线，得垂足a、b和a′、b′。线段ab 称为力F 在x 轴上的投影，用Fx 表示，线段a′b′称为力F 在y 轴上的投影，用Fy 表示。

pagenumber_ebook=41,pagenumber_book=32

图3-11　力在坐标轴上投影

若已知力F 的大小和它与x 轴间的夹角α（取锐角），则力F 在直角坐标轴上的投影Fx和Fy 分别为

pagenumber_ebook=41,pagenumber_book=32

如将F 沿直角坐标轴方向分解，所得分力Fx、Fy 的值与力F 在同轴上的投影Fx、Fy的绝对值相等。但须注意，力在轴上的投影是代数量，而分力是矢量，不可混为一谈。力的投影正负号规定如下：若由a 到b（或a′到b′）的指向与坐标轴的正向一致，则力的投影为正值；反之，为负值。

若已知Fx、Fy 值，可求出F 的大小和方向，即

pagenumber_ebook=41,pagenumber_book=32

2.平面汇交力系合成的解析法

设刚体上作用有一个平面汇交力系F1、F2、…、Fn，据式（3-1）有

将上式两边分别向x 轴和y 轴投影，即有

pagenumber_ebook=41,pagenumber_book=32

式（3-5）即为合力投影定理：力系的合力在某轴上的投影，等于力系中各力在同一轴上投影的代数和。

当平面汇交力系已知时，可以求出力系中各力在坐标轴上的投影，然后利用合力投影定理求出平面汇交力系的合力在坐标轴上的投影FRx=∑Fx、FRy=∑Fy，然后再将FRx、FRy 合成，就可得到合力FR 的大小为

若用α 表示合力FR 与x 轴所构成的锐角，则

pagenumber_ebook=42,pagenumber_book=33

合力的指向可由∑Fx 及∑Fy 的正负号决定。

必须指出，上述各公式只对直角坐标系成立。应用式（3-6）、式（3-7）计算合力大小和方向的方法，称为平面汇交力系合成的解析法。

案例3-4 求图3-12 所示平面汇交力系的合力。已知F1=500 N，F2=1 000 N，F3=600 N，F4=2 000 N。

分析：取正交坐标系，如图3-12 所示，据式（3-6）和式（3-7），合力FR 在x 、y轴上的投影为

pagenumber_ebook=42,pagenumber_book=33

再求合力FR 的大小及与x 轴所夹的锐角α：

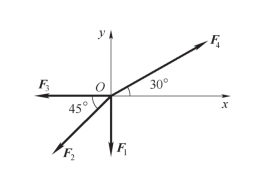
pagenumber_ebook=42,pagenumber_book=33

图3-12　案例3-4图

3.平面汇交力系平衡的解析条件

通过上面的讨论可知，平面汇交力系平衡的充分和必要条件是该力系的合力为零，用解析式表示为

式中，（∑Fx）2、（∑Fy）2 恒为正数，则要使FR=0，也只有(https://www.chuimin.cn)

pagenumber_ebook=43,pagenumber_book=34

所以，平面汇交力系平衡的充要条件为：力系中各力在两个坐标轴上投影的代数和均等于零。式（3-9）称为平面汇交力系的平衡方程，这是相互独立的两个方程，所以只能求解两个未知量。

案例3-5 图3-13（a）所示为一圆柱体置于夹角为α 的V 形槽内，并用压板D 夹紧。已知压板作用于圆柱体上的压力为F，试求槽面对圆柱体的约束反力。

分析：（1）取圆柱体为研究对象，画其受力图，如图3-13（b）所示。

（2）选取坐标系xOy 。

（3）列平衡方程式求解未知力，由式（3-7）得

pagenumber_ebook=43,pagenumber_book=34

由以上两式，解方程得

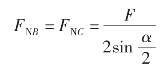
pagenumber_ebook=43,pagenumber_book=34

（4）讨论：由结果可知，FNB与FNC均随几何角度α 的变化而变化，角度α 越小，则压力FNB或FNC越大，因此，α 不宜过小。

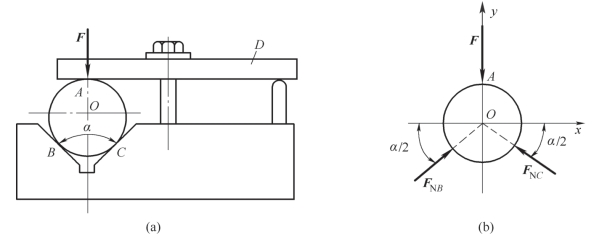
pagenumber_ebook=43,pagenumber_book=34

图3-13　案例3-5图

（a）夹具示意图；（b）工件受力图

案例3-6 重W=20 kN 的物体被绞车匀速吊起，绞车的绳子绕过光滑的定滑轮A[图3-14（a）]，滑轮由不计重力的杆AB、AC 支撑，A、B、C 三点均为光滑铰链。试求杆AB、杆AC 所受的力。

pagenumber_ebook=44,pagenumber_book=35

图3-14　绞车起吊重物

分析：（1）确定研究对象。由于AB、AC 两杆都是二力杆，假设AB 杆和AC 杆都受拉力、如图3-14（b）所示。为了求出这两个未知力，可通过求两杆对滑轮的约束反力来解决。因此取滑轮A 为研究对象。

（2）画受力图。滑轮受到绳子的拉力T1 和T2（已知T1=T2=W）。此外，杆AB 和AC对滑轮的约束反力为SAB和SAC。由于滑轮的大小可忽略不计，故这些力可看作是平面汇交力系。如图3-14（c）所示。

（3）列平衡方程。选取坐标轴，如图3-14（c）所示。为使未知力只在一个轴上有投影，在另外一个轴上的投影为零，坐标轴应尽量取在与未知力作用线垂直的方向，这样在一个平衡方程中只有一个未知数，不必解联立方程。

列平衡方程：

由

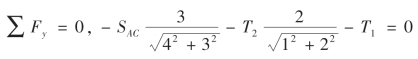
pagenumber_ebook=44,pagenumber_book=35

解得SAC=-63.2 kN。

由

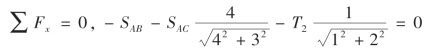
pagenumber_ebook=44,pagenumber_book=35

解得SAB=41.6 kN。

力SAC是负值，表示该力的假设方向与实际方向相反，因此杆AC 是受压杆。

通过以上的例题，可以归纳出解决平面汇交力系平衡问题的主要步骤和注意事项如下：

（1）确定研究对象，画受力图。一般以待求物体为研究对象，先画主动力再画被动力；正确应用二力平衡公理（二力杆）和力的多边形法则。

（2）选取适当的坐标系。原则是坐标轴尽量与未知力垂直，以减少未知力的个数。

（3）根据平衡条件列出平衡方程，要注意各力投影的正负号。

（4）求解未知量。解方程求出未知力，若求出的力为负值，则表示受力图上力的实际指向与所假设的指向相反。

平面力系合成的解析法及平衡条件

相关推荐