平面立体与曲面立体的表面交线,一般是由数段平面曲线组合而成的空间曲线,如图4-18所示。因此,求作平面立体与曲面立体的相贯线,可归结为求作平面与曲面立体的截交线和求直线(棱线)与曲面立体表面的交点。其中除左边的棱面AB完全与半球相交外,其他两个棱面只部分与半球相交。因此,本题只需再作出相贯线的正面投影及侧面投影即可。......
2025-09-29
立体的透视为立体表面的透视。作平面立体的透视实为作立体的棱线的透视。立体的形状由其表面的形状所决定。而平面立体表面的形状、大小和位置,由立体的棱线所决定。
6.3.4.1 交线法作形体的两点透视
【例6-6】 已知一方形体放在H 面上,其正投影为abcd,视点S在H 面上的正投影为s,如图6-13所示求形体的透视。
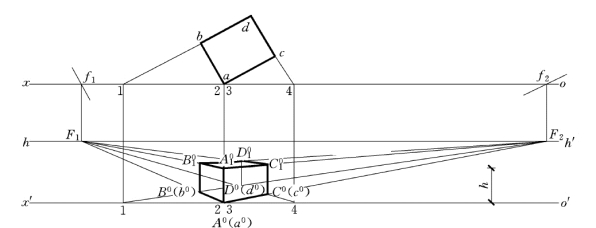
图6-13 交线法作正方体的透视
解:
(1)先作出其两个方面的灭点F1,F2。
(2)延长所有直线,交ox轴得各直线的迹点(1、2、3、4)。
(3)连接相应的迹点与灭点,得直线的全透视。
(4)因a在ox上,所以A0(a0)在o′x′轴上,其他各点的次透视亦可根据迹点进行判断而得到。
(5)过迹点2、3作竖直线,使A0A01=a′a′1,得A01。
![]()
【例6-7】 绘制台阶透视,如图6-14所示。
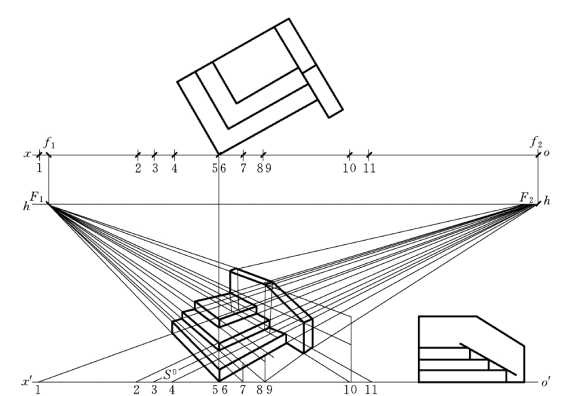
图6-14 台阶的透视作法
具体的作法不再详细写出,即先用交线法求出台阶的次透视,再分别求每一阶台阶的上下两个高度。这里要注意的是每一阶台阶必须求上下两个高度,还要作出台阶面上的可见部分。
【例6-8】 其他形体的透视求作举例,如图6-15~图6-17所示。
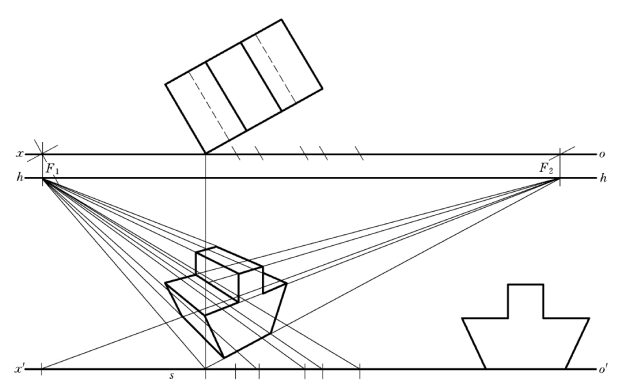
图6-15 斜面形体的透视作法
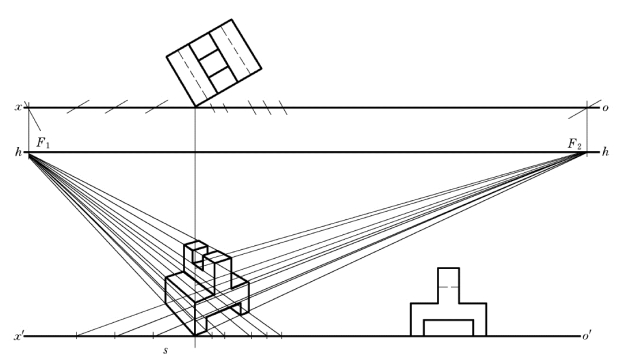
图6-16 复杂形体的透视作法
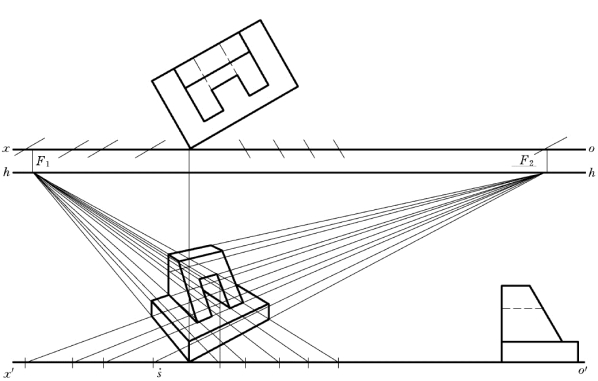
图6-17 复杂形体加斜面的透视作法(https://www.chuimin.cn)
6.3.4.2 H 面不能斜放时的透视 (交线法)
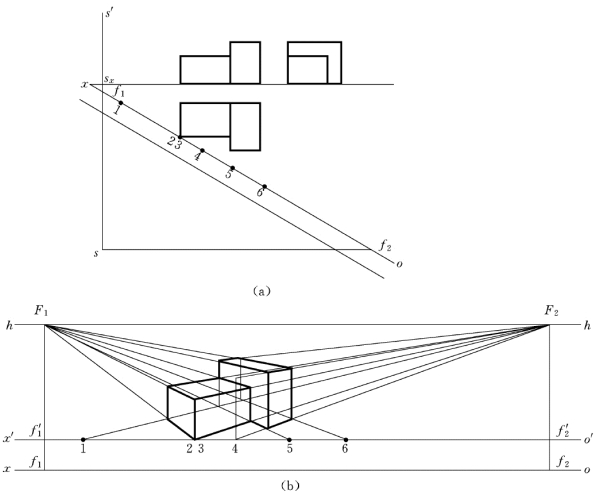
图6-18 交线法作图
(a)正面投影图;(b)透视作法
实际作透视图时,已知的房屋投影图位置如图6-18 (a)所示。该图中s′并非画面上主点,仅是V 面投影,sxs′表示视高。作图时,有时不便将H 面投影移置成倾斜位置,且透视图的上、下方没有布置斜放的H 面投影的位置。此时可以在原来的H 面投影上,作出站点s、ox并作出灭点在H 面上的正投影f1、f2和所有迹点(1~6)等点。然后将各点的相对距离移至图6-18 (b)所示的o′x′上。然后根据已知视高,定出o′x′和h—h,由o′x′上各点作竖直线来进行作图。方法可以参照上面的透视求法。
6.3.4.3 降低平面图法
作透视时,常因先作出的透视与H面上轮廓线的透视重叠而混淆不清,尤其用交线法作图时,如o′x′与h—h相距较近(视高较小时),因交线间夹角太小,常使交点位置不易准确。因此,如图6-19(a)所示,可取一个降低的水平投影面H1来作图。因H面投影在建筑工程中称为平面图,所以把这种降低H面投影称为降低平面图。这种作法称为降低平面图法。
空间状况如图6-19(a)所示,由于H面和H1平行,故直线AB的H1面投影a1b1与H面投影ab相同,故可利用原来的H面投影,仅使o1x1轴降低一些而已。因a1b1平行于ab,故有同一灭点F,且a01,a0,A0和b01,b0,B0及n1,n,N各在同一条竖直线上。
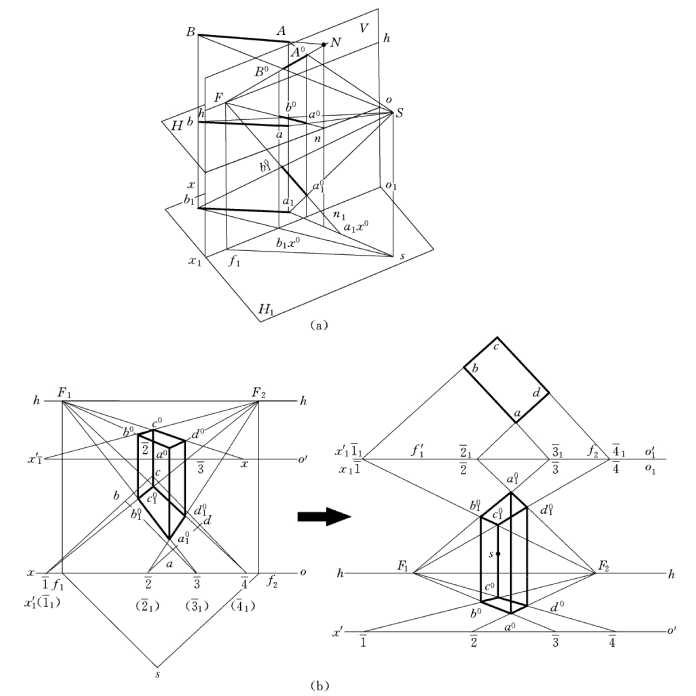
图6-19 降低平面法
先作一个降低平面,这里把这个降低平面放在与ox重合。

【例6-9】 已知一形体的俯视图和正视图如图6-20 (a)所示,1∶2求建筑形体的透视。
解:如原来的正投影图较小,若希望画出较大的透视图,除了把画面放得离开视点较远即把ox放得离开s较远,以获得较大透视外,也可如图将正投影图中的f1,f2,a及迹点等点之间的距离,按所需倍数放大。作图时,表现视高的o′x′与h—h间距离,以及真高线上的高度,应按同样倍数放大。
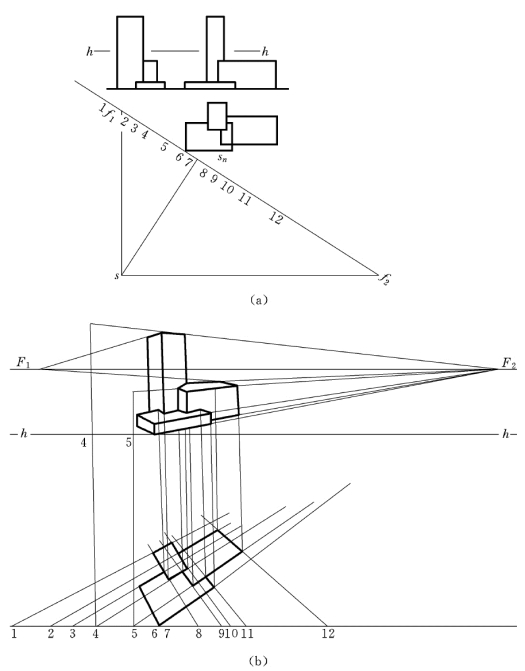
图6-20 降低平面法作图
(a)形体俯视图和正视图;(b)形体的求作
此题中的视高较小,可以使用降低平面法,具体的作图步骤不再具体写出。作出的图,如图6-20 (b)所示。
【例6-10】 已知一室内形体的俯视图,如图6-21 (a)所示,图纸比例为1∶100,视高为1500mm,房高为2800mm,1∶50求室内形体的透视。
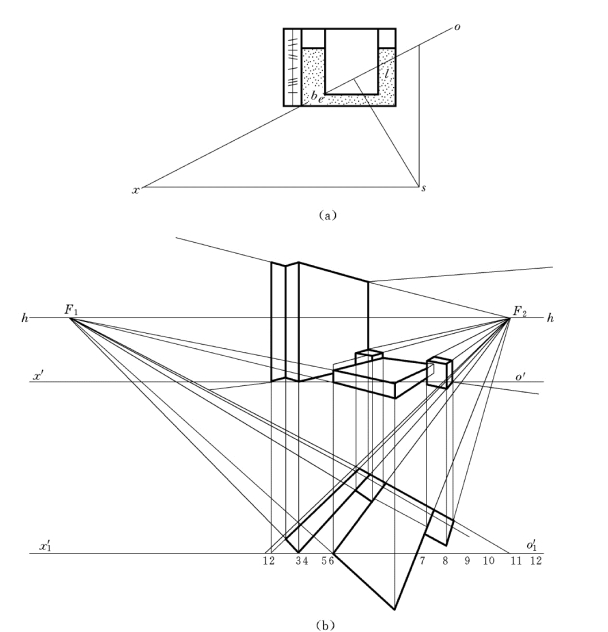
图6-21 室内形体的透视作法
(a)形体俯视图;(b)形体的求作
解:此题中的视高并不是很小,可以使用降低平面法,也可以直接作图,若使用降低平面则可以使作出的透视更加清晰。具体的作图步骤不再具体写出。作出的图如图6-21(b)所示。
相关文章

平面立体与曲面立体的表面交线,一般是由数段平面曲线组合而成的空间曲线,如图4-18所示。因此,求作平面立体与曲面立体的相贯线,可归结为求作平面与曲面立体的截交线和求直线(棱线)与曲面立体表面的交点。其中除左边的棱面AB完全与半球相交外,其他两个棱面只部分与半球相交。因此,本题只需再作出相贯线的正面投影及侧面投影即可。......
2025-09-29

图4-2求正垂面P与三棱锥的截交线解:从正面投影中可清楚地看到,截平面P与三棱锥的底面不相交,只与三个棱面相交。根据本题的特点,宜采用交点法作图。过1′、2′、3′向侧面引投影连接线,与s″a″、s″b″、s″c″相交,得1″、2″、3″。由于三棱锥各棱面的水平投影皆可见,故截交线的水平投影也都可见,画成实线;三棱锥侧面投影中SBC棱面不可见。......
2025-09-29

图2.1.3 在零件模型中创建关系Step1.先将工作目录设置至D:\proewf5.2\work\ch02.03,然后打开模型udf_place.prt。Step7.验证所创建的关系:改变d25的值,再生后,d27的值按关系式的约束自动改变。在装配中创建关系时,必须将各元件的进程标识作为后缀包括在尺寸符号中。......
2025-09-29

两平面立体相交,其相贯线在一般情况下是封闭的空间折线,但有时也会是平面多边形。从图4-17中可以看出,相贯线(折线)上任一段直线都是甲平面立体的一个棱面与乙立体的一个棱面的交线。因此,求作两平面立体相贯线,实质上仍归结为求直线与平面的交点,以及求平面与平面交线的问题。求直立三棱柱与水平三棱柱的相贯线,如图4-17所示。......
2025-09-29

选择单选按钮,可以在启用时,只显示被追踪点的正交追踪路径;选择单选按钮,可以将极轴角设置应用到,即此时可以按极轴角增量及附加角设置追踪指定点的路径。 利用正交和极轴功能完成图2-1的绘制。......
2025-09-29

图3-50输送单元的机械手示意图3)拖链装置当机械手装置做往复运动时,连接到机械手装置上的气管和电气连接线也随之运动,机械手装置上的所有气缸连接的气管和电线沿拖链带敷设,插接到电磁阀组上。图3-51输送单元的拖链装置图3-52输送单元的原点开关和极限开关示意图2.输送单元装置侧的安装输送单元装置侧的安装分为两部分:直线运动组件的安装、拖链的安装和机械手装置的安装。图3-54输送单元装置侧安装完成示意图......
2025-09-29
相关推荐