两直线的相对位置有以下三种：平行、相交、交叉。图2-43求相交两直线的投影已知图；作图解：根据相交直线的投影特点，可定出交点的V投影，利用交点可求出直线CD的V 投影。......
2025-09-29
截平面与圆柱的交点分析
【摘要】：平面截切圆柱时，由于截平面与圆柱的轴线相对位置不同，其截交线有三种不同的形状，如图4-4所示。当截平面倾斜于圆柱轴线时，它与圆柱面的截交线为一椭圆，如图4-4 所示。图4-4截平面与圆柱相交求正圆柱与正垂面P的截交线，如图4-5所示。且椭圆的正面投影积聚在截平面的正面迹线上；圆柱的水平投影有积聚性，故截交线的水平投影也为已知。
平面截切圆柱时，由于截平面与圆柱的轴线相对位置不同，其截交线有三种不同的形状，如图4-4所示。
（1）当截平面平行于圆柱轴线时，它与圆柱面的截交线为两条素线，如图4-4 （a）所示。
图4-3 用素线法和纬圆法求截交线上共有点
（2）当截平面垂直于圆柱轴线时，它与圆柱面的截交线为一纬圆，如图4-4 （b）所示。
（3）当截平面倾斜于圆柱轴线时，它与圆柱面的截交线为一椭圆（短轴垂直于圆柱轴线，其长度等于圆柱直径；长轴倾斜于圆柱轴线，其长度随截平面对圆柱轴线的倾斜程度而变化），如图4-4 （c）所示。
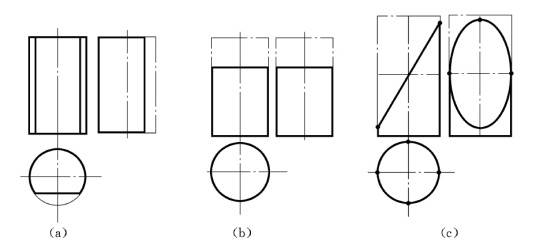
图4-4 截平面与圆柱相交
【例4-2】 求正圆柱与正垂面P的截交线，如图4-5所示。
解：由于正垂面P倾斜于圆柱轴线，故截交线为椭圆。且椭圆的正面投影积聚在截平面的正面迹线上（圆柱正面投影轮廓间的一段斜线）；圆柱的水平投影有积聚性，故截交线的水平投影也为已知（重影于圆柱的水平投影——圆）。因此，根据截交线的二已知投影便可求出截交线上若干点的侧面投影，从而完成截交线的作图。
作图步骤：(https://www.chuimin.cn)
（1）求特殊点。截交线上的特殊点一般是指：①曲面投影轮廓线上的点（很多情况下它们也是截交线各投影的可见性分界点）；②能够确定截交线投影范围的边界点，如截交线上的最高点与最低点，最前点与最后点，最左点与最右点等；③能够确定截交线投影几何形状的一些点（如椭圆的长、短轴的端点）。本例中轮廓线上的点 （1、2、3、4）可根据它们的正面投影作出其侧面投影1″、2″、3″、4″，其中1点和2点便是截交线上的最高点和最低点，如图4-6所示。
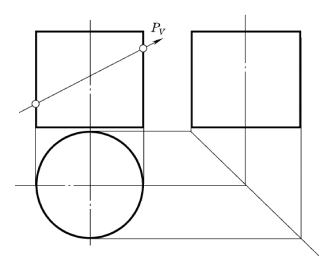
图4-5 正垂面与圆柱的截交
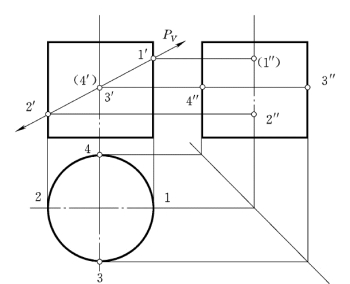
图4-6 求特殊位置点的截交线
根据对椭圆长、短轴的分析可知，垂直于正投影面的椭圆直径3、4等于该圆柱的直径，故3、4应是短轴；而与其垂直的直径1、2则是椭圆的长轴，该长轴恰好处在截平面内对水平面的最大斜度线的位置。根据直角投影特性，这一对长、短轴的侧面投影1″2″和3″4″仍应相互垂直。
（2）求一般点。在水平投影中在特殊点之间取四个对称位置的中间点5、6、7、8，先求它们的正面投影，然后再求出其侧面投影，如图4-7所示。
（3）连线并判别可见性。圆滑连接侧面投影中所求各点 （连接时注意椭圆曲线的对称性），其中3″、7″、1″、8″、4″段位于圆柱右半部，侧面投影为不可见，画成虚线。
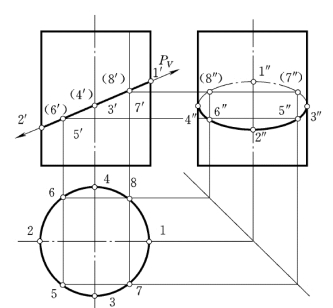
图4-7 求一般点的截交线
相关文章
- 详细阅读
-
平面几何分析的组成结构详细阅读
对一个平面体系进行几何组成分析时，其可能的最终结果共有四种情况：几何不变体系，且无多余约束；几何不变体系，且有多余约束；常变体系；瞬变体系。在进行平面体系的几何组成分析时，一定要注意每根杆件使用且只能使用一次。由三刚片规则可知，它们所组成的体系是几何不变体系，并且没有多余约束。试对图11-24所示的体系进行几何组成分析。......
2025-09-29
-
平面内点与直线的关系详细阅读
图2-52平面上的直线的投影规律2.5.3.2平面内与投影面平行的直线凡在平面内平行于某一投影面的直线，称为投影面的平行线，可分为以下三种情况。平面上与投影面倾角最大的直线称为最大斜度线。......
2025-09-29
-
电气总平面图和电气平面图的图线设计与标准详细阅读
电气总平面图和电气平面图宜采用3种及以上线宽绘制，以清楚地表示上述项目之间的关系。建筑电气专业的图线宽度应该根据图线的类型、比例和复杂程度，按现行国家标准《房屋建筑制图统一标准》的规定选用，并宜为0.5、0.7和1.0。表12-1 建筑电气制图图线、线型及线宽当采用b=0.7和0.5的线宽组时，0.25b细线分别为0.18和0.12，图线中的细线可采用0.18和0.13两种线宽，也可统一采用0.13这一种线宽。......
2025-09-29
-
分析平面运动刚体内各点速度详细阅读
实际分析中，总是以运动已知的点作为基点。平面图形绕基点转动的角速度和角加速度与基点位置无关。这称为“平面运动的速度合成法”或“基点法”。这是确定刚体平面运动图形内任意点速度的基本方法。......
2025-09-29
-
暂态电势与电抗的分析与应用详细阅读
图9-9暂态电势和暂态电抗的等值电路习惯上称E′q为暂态电势，它同励磁绕组的总磁链Ψf成正比。电势正比于磁链，由此可见，暂态电势E′q也是某种意义下的气隙电势，暂态电抗x′d则是某种意义下的定子漏抗。如果令便可将方程式改写成电势常称为暂态电抗后的电势。以上根据磁链平衡方程式导出了暂态电势和暂态电抗的表达式，并对这些参数的意义作了说明。暂态电势在运行状态发生突变瞬间能够守恒。......
2025-09-29
- 详细阅读
-
关于变量相关关系的探讨与分析详细阅读
以两个变量为例进行讨论。这种关系x与y的关系点杂乱无章，如图X3.15所示。相关关系，指两个变量x与y之间的关系介于完全相关和零相关之，这种关系x与y的关系点呈带状分布趋势，如图X3.16所示。图X3.15零相关示意图图X3.16相关关系示意图直线相关；曲线相关例如，流域年径流深与年降水量之间的关系，就是相关关系。......
2025-09-29
相关推荐