首页理论教育常用几何作图技巧大全

常用几何作图技巧大全

2025-09-29 理论教育版权反馈

【摘要】：图1-21过已知点作已知直线的平行线1.3.2.2过已知点作已知直线的垂直线过已知点作已知直线的垂直线的方法如下。图1-22过已知点作已知直线的垂直线先使45°三角板的一直角边与BC重合，再使其斜边紧靠另一三角板，如图1-22所示。图1-25已知外接圆求作正五边形1.3.2.6作圆内接任意正多边形作圆内接任意正多边形的方法如下。

1.3.2.1　过已知点作已知直线的平行线

过已知点作已知直线的平行线的方法如下。

（1）已知点A和直线BC，如图1-21 （a）所示。

（2）用第一块三角板的一边与BC重合，第二块三角板与它的另一边紧靠，如图1 21 （b）所示。

（3）推动第一块三角板至A点，画一直线即为所求，如图1-21 （c）所示。

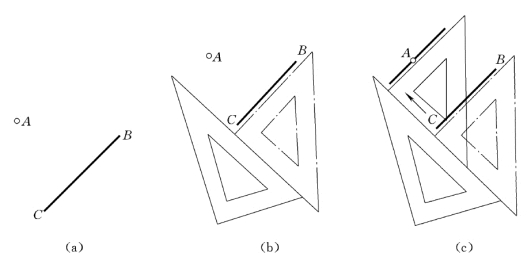
pagenumber_ebook=23,pagenumber_book=11

图1-21　过已知点作已知直线的平行线

1.3.2.2　过已知点作已知直线的垂直线

过已知点作已知直线的垂直线的方法如下。

（1）已知点A和直线BC，如图1-22 （a）所示。

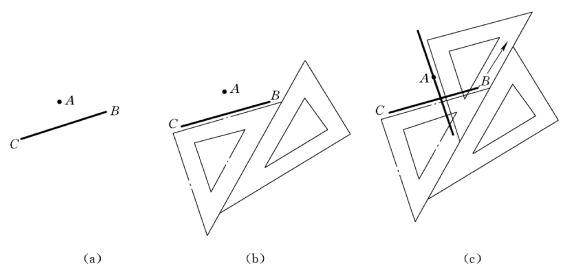
pagenumber_ebook=23,pagenumber_book=11

图1-22　过已知点作已知直线的垂直线

（2）先使45°三角板的一直角边与BC重合，再使其斜边紧靠另一三角板，如图1-22（b）所示。

（3）推动45°三角板，使另一直角边靠紧A 点，画一直线，即为所求，如图1-22（c）所示。

1.3.2.3　将已知线段任意等分

将已知线段任意等分的方法如下。

（1）已知直线AB，分AB为6等分，如图1-23 （a）所示。

（2）过A点作任意直线AC，在AC上任意截取6等分，标以1、2、3、4、5、6点，以第6点作为C点，并连接BC，如图1-23 （b）所示。

（3）分别过各等分点作BC的平行线交AB 得5个点，即分AB为6等分，如图1 23 （c）所示。

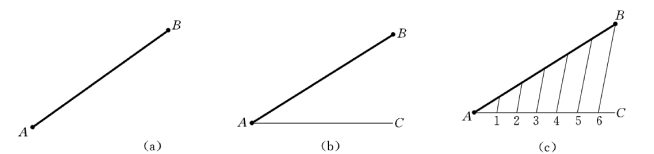
pagenumber_ebook=24,pagenumber_book=12

图1-23　将已知线段任意等分

1.3.2.4　将两行平行线间的距离任意等分(https://www.chuimin.cn)

将两行平行线间的距离任意等分的方法如下。

（1）已知平行线AB和CD，分其间距为6等分，如图1-24 （a）所示。

（2）将直尺上刻度的0点固定在AB上并以0为圆心摆动直尺，使刻度的5点落在CD上，在1、2、3、4、5各点处作标记，如图1-24 （b）所示。

（3）过各分点作AB的平行线即为所求，如图1-24 （c）所示。

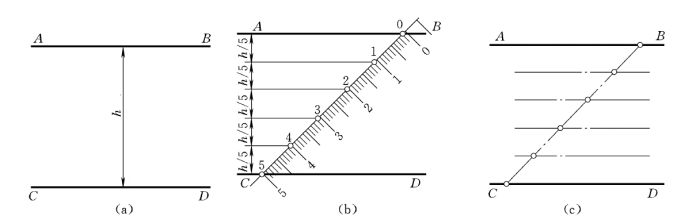
pagenumber_ebook=24,pagenumber_book=12

图1-24　将两平行线间的距离任意等分

1.3.2.5　已知外接圆求作正五边形

已知外接圆求作正五边形的方法如下。

（1）已知外接圆O，作内接正五边形，先平分半径OA，得平分点B，如图1-25 （a）所示。

（2）以B为圆心，B1为半径作弧交BO延长线于C，C1即为五边形的边长，如图1 25 （b）所示。

（3）以1为圆心，以C1为半径作弧，得2、5两点，如图1-25 （c）所示。

（4）分别以2、5点为圆心，以C1为半径在圆弧上截取3、4两点。顺次连接各点，即得正五边形，如图1-25 （d）所示。

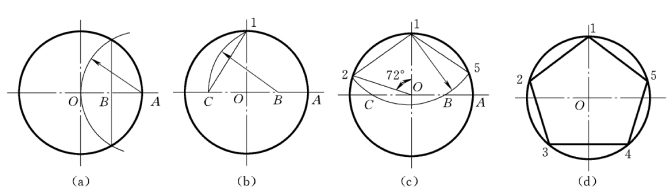
pagenumber_ebook=25,pagenumber_book=13

图1-25　已知外接圆求作正五边形

1.3.2.6　作圆内接任意正多边形

作圆内接任意正多边形的方法如下（现以正七边形为例）。

（1）已知外接圆，作内接正七边形，先将直径AB 分成为7等分，如图1-26（a）所示。

（2）以B为圆心，AB为半径，画圆弧与DC延长线相交于E，再自E引直线与AB上每隔一分点（如2、4、6）连接，并延长与圆周交于F、G、H 等点，如图1-26 （b）所示。

（3）求F、G和H 的对称点K、J和I，并顺次连接F、G、H、I、K、A等点即得正七边形，如图1-26 （c）所示。

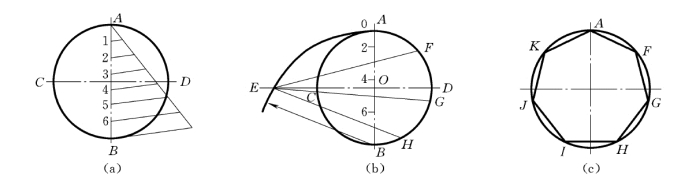
pagenumber_ebook=25,pagenumber_book=13

图1-26　作圆内接正七边形