GIP称为杆件的抗扭刚度，它反映杆件抵抗扭转变形的能力。由得按刚度条件确定d。要使轴同时满足强度和刚度条件，需取轴的直径d＝52mm。......
2025-09-30
建筑力学（第3版）：矩形截面杆自由扭转
【摘要】：在建筑结构中，矩形截面受扭杆一般都处于约束扭转状态。但是，由于约束扭转所引起的正应力可忽略不计，所以可按自由扭转的情况进行计算。这里直接给出矩形截面扭转轴的弹性力学解释的结论：矩形截面扭转轴的横截面上仍然只有剪应力，虽有正应力，但只要h/b的值不太大，正应力的数值很小，可忽略不计。横截面上的最大剪应力发生在长边的中点处。单位长度扭转角全轴的扭转角
在建筑结构中，矩形截面受扭杆一般都处于约束扭转状态。但是，由于约束扭转所引起的正应力可忽略不计，所以可按自由扭转的情况进行计算。这里直接给出矩形截面扭转轴的弹性力学解释的结论：
（1）矩形截面扭转轴的横截面上仍然只有剪应力，虽有正应力，但只要h/b的值不太大，正应力的数值很小，可忽略不计。
（2）截面周边上各点处的剪应力的方向与周边平行（相切），并形成与截面上扭矩相同转向的剪应力流，如图8-23（c）所示，剪应力的大小均呈非线性变化，中点处的剪应力最大。
（3）截面两条对称轴上各点处剪应力的方向都垂直于对称轴，其他线上各点的剪应力则是程度不同的倾斜。
（4）截面中心和四个角点处的剪应力等于零。
（5）横截面上的最大剪应力发生在长边的中点处。其计算公式为
式中 Wt——相当抗扭截面模量；
h——矩形截面长边的长度；
b——矩形截面短边的长度；
T——截面上的扭矩；
β——与截面尺寸的比值h/b有关的系数，可由表8-1查得。
短边中点处的剪应力也相当大，其计算公式为
式中 γ——与截面尺寸的比值h/b有关的系数，可由表8-1查得。
单位长度扭转角θ为
式中 α——与截面尺寸的比值h/b有关的系数，可由表8-1查得；(https://www.chuimin.cn)
G——材料的剪切弹性模量。
表8-1 矩形截面杆纯扭转时的系数α、β和γ
【例8-6】 矩形截面杆的尺寸及荷载如图8-24所示，材料的剪切弹性模量G＝0.55×103MPa，求：（1）横截面最大剪应力；（2）短边中点处的剪应力；（3）扭转角。
图8-24
【解】 （1）轴内各横截面的扭矩相等，T＝100N·m。
由
＝1.375，查表8-1（插值法）得
因各横截面的剪应力分布相同，最大剪应力发生在长边中点。
（2）短边中点处的剪应力。
（3）扭转角。
单位长度扭转角
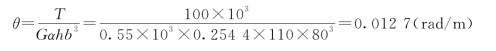
全轴的扭转角
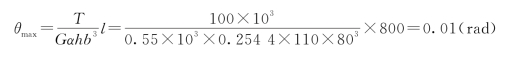
相关文章
- 详细阅读
-
轴向拉（压）杆横截面上的应力|建筑力学（第3详细阅读
由此可得，横截面上各点处的正应力σ大小相等[图7-7]。若杆的轴力为N，横截面面积为A，则正应力为应力的单位为帕斯卡（简称帕），1帕＝1牛顿/平方米，或表示为1Pa＝1N/m2。由于前面已规定了轴力的正负号，由式（7-1）可知，正应力也随轴力N而有正负之分，即拉应力为正，压应力为负。直杆的横截面面积A＝10cm2，试计算各段横截面上的正应力。图7-8用截面法求出各段轴力：由式（7-1）计算各段的正应力值为......
2025-09-30
-
圆轴扭转内力扭矩-建筑力学（第3版）详细阅读
在对圆轴进行强度计算之前先要计算出圆轴横截面上的内力——扭矩。根据平衡条件可知，C截面上必存在一个内力偶矩T，与外力偶矩m使左半部保持平衡。此内力偶矩称为扭矩，用T表示。扭矩的单位与力矩相同，常用N·m或kN·m。图8-12与计算轴力的方法类似，用截面法计算扭矩时，通常假定扭矩为正。用截面法分别求出各段上的扭矩。......
2025-09-30
-
圆轴扭转剪应力分布-《建筑力学（第3版）》详细阅读
为解决圆轴扭转的强度问题，在求得横截面上的扭矩之后，还要进一步研究横截面上的应力。在整个横截面上，所有这些微力矩之和应等于该截面的扭矩T，因此将式代入得积分即为横截面的极惯性矩，因而式可改写为将式代入式得这就是圆轴扭转时横截面上的剪应力计算公式。式中，T为横截面上的扭矩；IP为圆截面对圆心的极惯性矩；ρ为所求应力点至圆心的距离。因这里的剪应力正、负无实用意义，一般只计算其绝对值。......
2025-09-30
-
建筑力学研究任务和内容，建筑力学第3版详细阅读
建筑力学的任务是研究结构的几何组成规律，以及在荷载作用下结构和构件的强度、刚度和稳定性问题。具体来说，建筑力学将讨论下列几个方面的内容：力系的简化和力系平衡问题。......
2025-09-30
-
建筑力学（第3版）：轴力图制作详细阅读
当杆件受到多于两个轴向外力的作用时，在杆件的不同横截面上轴力不尽相同。将描述沿杆长各个横截面上轴力变化规律的图形，称为轴力图。画轴力图时，将正的轴力画在轴线上方，负的轴力画在轴线下方。根据上面求出的各段杆轴力的大小及其正负号画出轴力图，如图7-6所示。画轴力图时应注意以下几点：轴力图要与计算简图对齐。标明正负号和数值。在画轴力图时，也可用一条基线表示横截面位置。......
2025-09-30
-
建筑力学书中的杆件形变与度量详细阅读
图0-5图0-6等截面杆；变截面杆2.杆件变形的基本形式杆件受外力作用后，其几何形状和尺寸一般都要发生改变，这种改变量称为变形。杆件在不同形式的外力作用下，将发生不同形式的变形。总的来说，杆件变形的基本形式有以下四种：轴向拉伸或压缩[图0-7、]。图0-8所示为微小正六面体。上述微小正六面体的各边缩小为无穷小时，通常称为单元体。......
2025-09-30
- 详细阅读
相关推荐