为了形象地表明沿梁轴线各横截面上剪力和弯矩的变化情况，通常将剪力和弯矩在全梁范围内变化的规律用图形来表示，这种图形称为剪力图和弯矩图。对于非水平梁而言，剪力图可以作在梁轴线的任一侧，并标明正、负号；弯矩图作在梁受拉的一侧。根据剪力方程和弯矩方程判断剪力图和弯矩图的形状，确定控制截面的个数及内力值，作图。在集中力偶作用处，剪力图无变化，弯矩图不连续，发生突变，突变的绝对值等于集中力偶的力偶矩数值。......
2025-09-29
载荷集度与剪力、弯矩的微分关系及应用
【摘要】：根据上述微分关系，可以得到下述推论，这些推论对正确绘制或校核剪力图和弯矩图有很大的帮助。因此，对于受均布载荷作用的一段梁上，其剪力图为一倾斜直线，而弯矩图为抛物线。在集中力作用截面的左、右两侧，剪力FQ 有一突然变化，弯矩图的斜率也发生突然变化，成为一个折点。表7-1梁的剪力图和弯矩图的规律案例7-5 外伸梁及其所受载荷如图7-16所示，试作梁的剪力图和弯矩图。
从上面几个例题可以看出，由于载荷不同，梁的剪力图和弯矩图也就不同；在案例7-4中曾经指出，在FQ=0 的截面上，弯矩有极值等。这些都说明载荷、剪力、弯矩间存在着一定关系，下面来分析这种关系。
轴线为直线的梁[图7-15（a）]，受载荷作用，其中坐标轴的原点位于梁的左端，y轴向上为正，梁上分布载荷的集度q（x）是x 的连续函数，并规定向上为正。为了研究剪力、弯矩沿梁轴的变化情况，用横截面m-m 和n-n 从梁中截取一微段dx 来分析[图7-15（b）]，有分布载荷q（x）和两端截面上的剪力、弯矩。由于所取的dx 为微量，故可把q（x）看成是均布载荷。
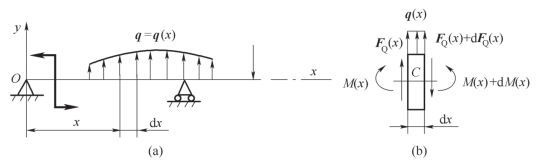
图7-15 简支梁
在这些力的作用下，微段处于平衡状态。由平衡方程∑Fy=0 和∑MC=0，得
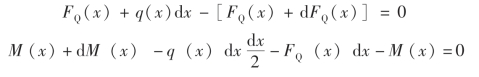
略去第二式中的高阶微量
，得
这就是直梁微段的平衡方程。由式（7-1）和式（7-2）可进一步得到
式（7-1）～式（7-3）表示了直梁的q（x）、FQ（x）和M（x）间的微分关系。
根据上述微分关系，可以得到下述推论，这些推论对正确绘制或校核剪力图和弯矩图有很大的帮助。
（1）在梁的某一段内，若无分布载荷作用，即q（x）=0，由式（7-1）可知，在该段梁上FQ（x）=常数，剪力图是平行于x 轴的直线。再由式（7-2）可得M（x）是x 的线性函数，其弯矩图为一倾斜直线。
（2）在梁的某一段内，若作用着均布载荷，即q（x）=常数，由式（7-3）可知，FQ（x）为x 的线性函数，M（x）为x 的二次函数。因此，对于受均布载荷作用的一段梁上，其剪力图为一倾斜直线，而弯矩图为抛物线。
在梁的某一段内，若分布载荷q（x）向下，这表明弯矩图应为向上凸的曲线；反之，若分布载荷向上，则弯矩图应为向下凹的曲线。
（3）若在梁的某一截面上FQ（x）=0，则在这一截面上弯矩具有一极值（极大或极小），即弯矩的极值发生于剪力为零的截面上（案例7-4）。
在集中力作用截面的左、右两侧，剪力FQ 有一突然变化，弯矩图的斜率也发生突然变化，成为一个折点。弯矩的极值就可能出现于这类截面上（案例7-2）。
在集中力偶作用截面的左、右两侧，弯矩发生突然变化（案例7-3），这也可能出现弯矩的极值。
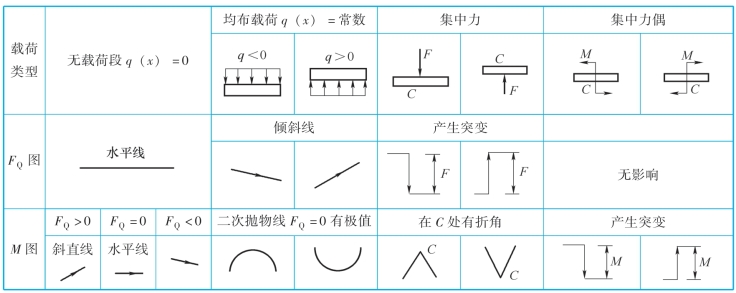
根据集中力、集中力偶作用处内力图的变化规律，可以将剪力图、弯矩图和梁上载荷三者之间的一些常见的规律小结如表7-1 所示。(https://www.chuimin.cn)
表7-1 梁的剪力图和弯矩图的规律
案例7-5 外伸梁及其所受载荷如图7-16（a）所示，试作梁的剪力图和弯矩图。
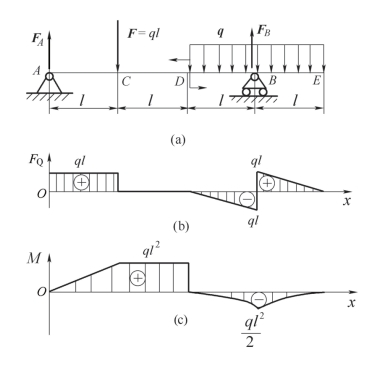
图7-16 外伸梁
分析：（1）由平衡方程求得支座反力为
（2）绘制剪力图。A 截面上有向上的支座反力FA，因此A 截面的剪力有突变，突变值为ql。AC 段梁上无载荷，剪力为常量，即FQ=ql。C 截面有向下的集中力F=ql，剪力有突变，故C 截面右侧的剪力FQ=ql-ql=0。CD 段无载荷，所以剪力为常量FQ=0。DB 段有均布载荷，剪力图为斜直线，B 截面左侧剪力FQ=-ql。B 截面有支座反力，剪力有突变，突变值为2ql，故截面右侧剪力FQ=2ql-ql=ql。BE 段有均布载荷，剪力图为斜直线，E截面剪力为零。因此可作出剪力图，如图7-16（b）所示。
（3）绘制弯矩图。A 截面上弯矩MA=0，AC 段上剪力为常量，故弯矩图为斜直线，C 截面上的弯矩M=ql2。CD 段上剪力为零，故弯矩图为与轴线平行的直线。D 截面有集中力偶作用，弯矩有突变，突变值为ql2，故D 截面右侧弯矩M=ql2-ql2=0。DB 和BE 段上有均布载荷q，弯矩图为抛物线，D 截面右侧与E 截面上的剪力FQ=0，所以D 截面和E 截面的弯矩有极值，且均为极小值零，B 截面上有支座反力，故弯矩图上有折点，大小为ql2/2。从而可作弯矩图，如图7-16（c）所示。
案例7-6 迅速绘制如图7-17 所示的简支梁的剪力图和弯矩图。
分析：（1）求支座反力，列平衡方程如下
∑MA（F）=0 FB×3-32-40×1=0 得FB=24 kN
∑Fy=0 FA+FB-40=0 得FA=16 kN
（2）剪力图的绘制。
从坐标原点开始画，A 处有集中力FA=16 kN，剪力图向上突变到16 kN。AC 段无载荷，剪力图为一平行于x 轴的直线。C 截面有向下的集中力40 kN，剪力图向下突变到-24 kN（16-40=-24），D 处有集中力偶，但不影响剪力，故CB 段为平行于x 的一条直线。支座B 处有向上的支座反力FB=24 kN，故剪力图向上突变回到零点。
（2）弯矩图的绘制。
从原点开始画起，AC 段为无载荷段，且由AC 段的FQ ＞0，故AC 段的弯矩图为一向上倾斜的直线，到C 截面，弯矩值为MC=FA ×1 m=16 kN·m。CD 段为无载荷段，且由CD 段的FQ ＜0，故CD 段的弯矩图为一向下倾斜的直线，到D 截面左侧，弯矩MD-=-8 kN·m。D 截面上有一顺时针转向的力偶，故在D 截面上弯矩图向上突变，由-8 kN·m 变为24 kN·m（-8 kN·m+32 kN·m=24 kN·m）。DB 段为无载荷段，且DB 段的FQ ＜0，故DB 段的弯矩图为一向下倾斜的直线，最后回到零点。
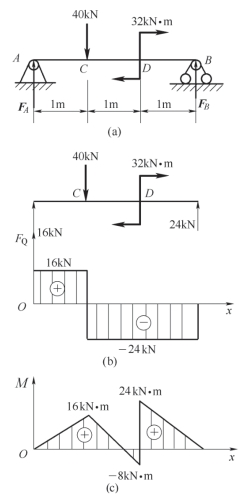
图7-17 简支梁
相关文章
- 详细阅读
- 详细阅读
-
固态继电器的参数及应用实例详细阅读
工作原理光耦合式固态继电器的原理图见图1-31。图1-31 光电耦合式固态继电器工作原理图选用固态继电器的主要参数有输入电压和电流、输出电压和电流、输出漏电流等。图1-32 固体继电器应用实例......
2025-09-29
-
模拟信号与数字信号的区别及应用详细阅读
模拟信号与数字信号都是无线电和电视广播中的电磁波，用于传播音频信息和视频信息，但两者有较大的差别。模拟信号的主要缺点是会受杂波的影响，噪声效应会使信号损坏，损坏后的模拟信号几乎不可能再次还原。误码是指数字信号在传输过程中，因某种干扰使接收端的再生码元可能出的错误。误码的多少与原始正常信号的比值则为误码率。有关模拟信号和数字信号的相关知识，这里因篇幅所限就只做些简要介绍。......
2025-09-29
-
时尚与个体的相互关系详细阅读
西美尔认为时尚外在于个体，时尚向个体展现的易变性是个体自我稳定感的对照，在对照中，个体的自我感意识到自身的相对持续性。随后西美尔对于时尚与个体、时尚与阶级之间关系的论述都是以上面两点为基础和前提的。西美尔认为，作为一种大众行为，时尚可以帮助个体克服羞耻感。在接下来关于时尚与个体关系的论述中，西美尔强调了个体的心理因素对于个人时尚和社会时尚的影响。......
2025-09-29
-
电气回路标号的原理及应用详细阅读
在电气图中，用于表示回路种类、特征的文字和数字标号称为回路标号。交流二次回路的标号原则与直流二次回路相似。在二次回路中，除电气元器件、设备、线路标注文字符号外，为简明起见，其他只标注回路标号。......
2025-09-29
-
力矩与点的关系详细阅读
图3-16力对点的矩实例脚蹬自行车；羊角锤拔钉子；开、关门；扳手拧螺母由经验可知，力的这种转动作用不仅与力的大小、方向有关，还与转动中心至力的作用线的垂直距离d 有关。互成平衡的两个力对于同一点的矩的代数和等于零。......
2025-09-29
-
蛋的构造与保质关系详细阅读
浓厚蛋白与蛋的质量、贮藏、加工有着密切的关系，含有溶菌酶，它具有溶解微生物膜的特性，因此有抑制和杀灭侵入的微生物的作用。随着蛋存放时间的延长，或受外界较高气温等因素的影响，溶菌酶也逐渐减少，以至完全消失，蛋便失去了抑菌和杀菌的能力，此时侵入蛋内的微生物便生长繁殖，使蛋发生腐败变质。稀薄蛋白约占蛋白总量的 45% 左右，呈水样胶体，不含溶菌酶。淡卵黄柱向外延伸至蛋黄膜下，其喇叭形的口部托着胚珠。......
2025-09-29
相关推荐