由式(5-1)可知,拉(压)杆的工作应力,为了保证构件能安全正常地工作,则杆内最大的工作应力不得超过材料的许用应力。即式(5-8)称为拉(压)杆的强度条件。在轴向拉(压)杆中,产生最大正应力的截面称为危险截面。应用强度条件式(5-8)可以解决轴向拉(压)杆强度计算的三类问题。如,表示杆件的强度是满足要求的,否则不满足强度条件。......
2025-09-29
当压杆中的应力达到(或超过)其临界应力时,压杆会丧失稳定。因此,正常工作的压杆,其横截面上的应力应小于临界应力。在工程中,为了保证压杆具有足够的稳定性,还必须考虑一定的安全储备,这就要求横截面上的应力不能超过压杆的临界应力的许用值[σcr],即
![]()
[σcr]为临界应力的许用值,其值为

式中 nst——稳定安全系数。
稳定安全系数一般都大于强度计算时的安全系数,这是因为在确定稳定安全系数时,除了应遵循确定安全系数的一般原则以外,还必须考虑实际压杆并非理想的轴向压杆这一情况。例如,在制造过程中,杆件不可避免地存在微小的弯曲(即存在初曲率);另外,外力的作用线也不可能绝对准确地与杆件的轴线相重合(即存在初偏心)等,这些因素都应在稳定安全系数中加以考虑。
为了计算上的方便,将临界应力的许用值,写成如下形式:
![]()
从上式可知,φ值为
![]()
式中 [σ]——强度计算时的许用应力;
φ——折减系数,其值小于l。
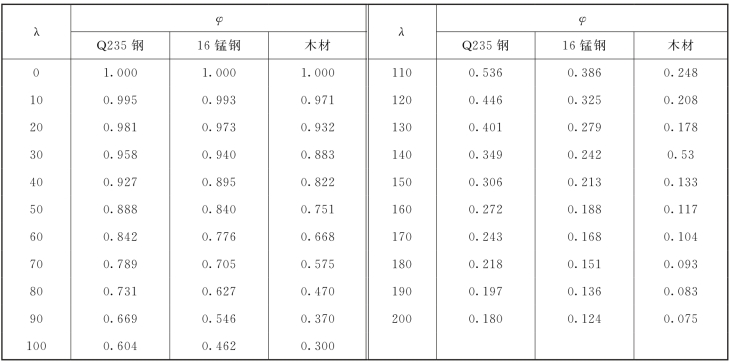
由式(9-12)可知,当[σ]一定时,φ取决于σcr与nst。由于临界应力σcr值随压杆的长细比λ而改变,而不同长细比的压杆一般又规定不同的稳定安全系数,所以折减系数φ是长细比λ的函数。当材料一定时,φ值取决于长细比λ的值。表9-3即列出了Q235钢、16锰钢和木材的折减系φ数值。
[σcr]与[σ]虽然都是“许用应力”,但两者却有很大的不同。[σ]只与材料有关,当材料一定时,其值为定值;而[σcr]除了与材料有关以外,还与压杆的长细比有关,因此,相同材料制成的不同(长细比)的压杆,其[σcr]值是不同的。
将式(9-9)代入式(9-10),可得
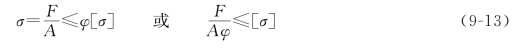
上式即为压杆需要满足的稳定条件。由于折减系数φ可按λ的值直接从表9-3中查到,因此,按式(9-13)的稳定条件进行压杆的稳定计算,十分方便。因此,该方法也称为实用计算方法。
表9-3 折减系数表
应当指出,在稳定计算中,压杆的横截面面积A均采用毛截面面积计算,即当压杆在局部有横截面削弱(如钻孔、开口等)时,可不予考虑。因为压杆的稳定性取决于整个杆件的弯曲刚度,而局部的截面削弱对整个杆件的整体刚度来说,影响甚微。但是,对截面的削弱处,则应当进行强度验算。
应用压杆的稳定条件,可以对以下三个方面的问题进行计算:
(1)稳定校核,即已知压杆的几何尺寸、所用材料、支承条件以及承受的压力,验算是否满足式(9-13)的稳定性。
这类问题,一般应首先计算出压杆的长细比λ,根据λ查出相应的折减系数φ,再按照式(9-13)进行校核。
(2)计算稳定时的许用荷载,即已知压杆的几何尺寸、所用材料及支承条件,按稳定条件计算其能够承受的许用荷载F值。
这类问题,一般也要首先计算出压杆的长细比λ,根据λ查出相应的折减系数φ,再按照下式进行计算。
F≤Aφ[σ]
(3)进行截面设计,即已知压杆的长度、所用材料、支承条件以及承受的压力F,按照稳定条件计算压杆所需的截面尺寸。
这类问题,一般采用“试算法”。这是因为在稳定条件[式(9-13)]中,折减系数φ是根据压杆的长细比λ查表得到的,而在压杆的截面尺寸尚未确定之前,压杆的长细比λ不能确定,所以也就不能确定折减系数φ。因此,只能采用试算法。首先假定一折减系数值φ(0与1之间),由稳定条件计算所需要的截面面积A,然后计算出压杆的长细比λ,根据压杆的长细比λ查表得到折减系数φ,再按照式(9-8)验算是否满足稳定条件。如果不满足稳定条件,则应重新假定折减系数φ,重复上述过程,直到满足稳定条件为止。
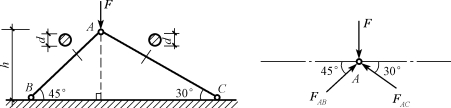
【例9-3】如图9-6所示,构架由两根直径相同的圆杆构成,杆的材料为Q235钢,直径d=20mm,材料的许用应力[σ]=170MPa,已知h=0.4m,作用力F=15kN。试在计算平面内校核两杆的稳定性。
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
图9-6 例9-3图
解:(1)计算各杆承受的压力。取结点A为研究对象,根据平衡条件列方程
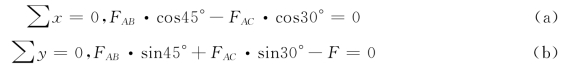
联立式(a)、式(b)解得两杆承受的压力分别为
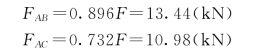
(2)计算两杆的长细比。各杆的长度分别为
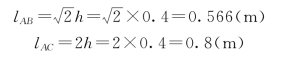
则两杆的长细比分别为
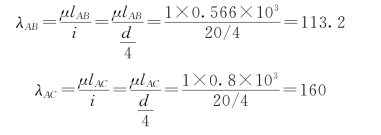
(3)由表9-3查得折减系数为
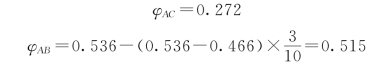
(4)按照稳定条件进行验算。
AB杆
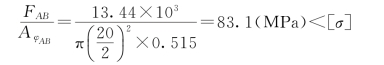
AC杆
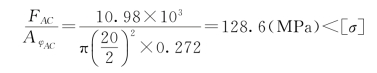
因此,两杆都满足稳定条件,构架稳定。
【例9-4】如图9-7所示支架,BD杆为正方形截面的木杆,其长度l=2m,截面边长a=0.1m,木材的许用应力[σ]=10MPa,试从满足BD杆的稳定条件考虑,计算该支架能承受的最大荷载Fmax。
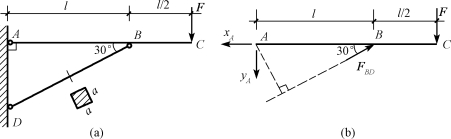
图9-7 例9-4图
解:(1)计算BD杆的长细比。
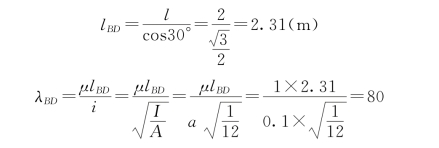
(2)求BD杆能承受的最大压力。根据长细比λBD查表9-3,得φBD=0.470,则BD杆能承受的最大压力为
FBDmax=Aφ[σ]=0.12×106×0.470×10=47×103N=47(kN)
(3)根据外力F与BD杆所承受压力之间的关系,求出该支架能承受的最大荷载Fmax。考虑AC的平衡,可得
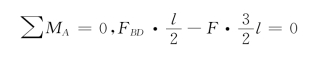
从而可求得
![]()
因此,该支架能承受的最大荷载Fmax为
![]()
相关文章

由式(5-1)可知,拉(压)杆的工作应力,为了保证构件能安全正常地工作,则杆内最大的工作应力不得超过材料的许用应力。即式(5-8)称为拉(压)杆的强度条件。在轴向拉(压)杆中,产生最大正应力的截面称为危险截面。应用强度条件式(5-8)可以解决轴向拉(压)杆强度计算的三类问题。如,表示杆件的强度是满足要求的,否则不满足强度条件。......
2025-09-29

于是临界应力可写为令则上式为计算压杆临界应力的欧拉公式,式中λ称为压杆的柔度。从式(9-3)还可以看出,压杆的柔度值越大,则其临界应力越小,压杆就越容易失稳。因此,欧拉公式的适用范围应当是压杆的临界应力σcr不超过材料的比例极限σP,即有若设λP为压杆的临界应力达到材料的比例极限σP时的柔度值,则故欧拉公式的适用范围为上式表明,当压杆的柔度不小于λP时,才可以应用欧拉公式计算临界力或临界应力。......
2025-09-29

图3-20 结构优化后,打击杆的应力应变分布云图与1688号节点的应力应变时间历程曲线a)应力分布云图与1688号节点的应力时间历程曲线 b)应变分布云图与1688号节点的应变时间历程曲线结构优化后,打击杆分别选用A3钢、调质45钢和调质40Cr时的寿命分布云图如图3-21所示,可见:1)结构优化后的打击杆中间部分寿命较长,原打击杆中间凸台部分的薄弱环节已经消除,这是由于结构优化后的打击杆中间部分为一整个圆柱,应力集中现象消除。......
2025-09-29

对冗余系统可以进行远程运行、远程停止、远程暂停、远程锁存清除、远程复位等操作,与通信路径无关。对冗余系统进行远程操作的方法有4种:从GX Developer执行的远程操作、MELSEC-NET/H网模块的专用指令进行的远程操作、根据MC协议进行的远程操作、通过EZSocket的OPS进行的远程操作。......
2025-09-29

图7-21 热稳定性计算流程图最后,总载荷时间超过1s,计算结束,获得各个载荷步内电流有效值、导体温度、电动斥力矩、侧偏力矩和滑动力矩的分布规律。此外,为了考虑短时耐受过程初始阶段暂态电流对热稳定性的影响,依据三相暂态电流表达式,利用等效原则,将60ms时间内各个载荷步内短路电流换算为正弦电流进行加载。......
2025-09-29

图7-6 动导电杆电动斥力示意图图7-7 软连接受力示意图各动导电杆不仅可能会受到电动斥力的作用而发生斥开,还会在侧向电动力的作用下发生触头侧偏和触头滑移等破坏电接触稳定性的现象。由于短路电流暂态分量的缘故,三相断路器电流在20ms内相继达到各相最大值,因而短路电流作用的前20ms时间内是电动稳定性研究的重点。......
2025-09-29

短路电流初始阶段根据上一小节分析可知,合闸相角为φ+π/6时,触头系统电动稳定性最差,故本节主要分析合闸相角为φ+π/6时频率对电动稳定性的影响。增大的冲击系数,势必会对短耐过程中电动稳定性造成影响。因此,如何采取措施抑制频率升高后电流的不均匀性,以及提高外侧动导电杆的动热稳定性是提高非工频框架断路器短时耐受能力的关键点之一。......
2025-09-29

返回导轨与工作导轨不同,施加到导轨上的载荷几乎是固定的,梯级自重载荷Ws均等分布在4个梯级滚轮上,一个梯级距的梯级链重量的载荷Wc均匀分布在梯级主轮上。因返回主轮导轨和副轮导轨是分离设置的,下面以受力较大的主轮返回导轨为例讲解强度校核。要注意的是返回导轨的上曲线段与工作导轨上曲线段类似的法线张力,因此有必要对其进行强度和磨损分析,方法与工作导轨上曲线区段相同。......
2025-09-29
相关推荐