要解决轴向拉压杆的强度问题，不但要知道杆件的内力，还必须知道内力在截面上的分布规律。下面用这种方法推导轴向拉压杆的应力计算公式。由于拉压杆的轴力是垂直于横截面的，故与它相应的分布内力也必然垂直于横截面，由此可知，轴向拉杆横截面上只有正应力，而没有剪应力。由此可得出结论：轴向拉伸时，杆件横截面上各点处只产生正应力，且大小相等[图5-9]，即式中 N——杆件横截面上的轴力；A——杆件的横截面面积。......
2025-09-29
欧拉公式：细长压杆临界力计算方法
【摘要】：下面介绍不同约束条件下压杆的临界力计算公式。两端铰支细长杆的临界力计算公式——欧拉公式。从欧拉公式可以看出，细长压杆的临界力Fcr与压杆的弯曲刚度成正比，而与杆长l的平方成反比。杆端为其他约束的细长压杆，其临界力计算公式可参考前面的方法导出，也可以采用类比的方法得到。经验表明，具有相同挠曲线形状的压杆，其临界力计算公式也相同。
从上述讨论可知，压杆在临界力作用下，其直线状态的平衡将由稳定的平衡转变为不稳定的平衡，此时，即使撤去侧向干扰力，压杆仍然将保持在微弯状态下的平衡。当然，如果压力超过这个临界力，弯曲变形将明显增大。因此，使压杆在微弯状态下保持平衡的最小的轴向压力，即为压杆的临界压力。下面介绍不同约束条件下压杆的临界力计算公式。
（1）两端铰支细长杆的临界力计算公式——欧拉公式。
设两端铰支长度为z的细长杆，在轴向压力Fcr的作用下保持微弯平衡状态，如图9-2所示。杆在小变形时其挠曲线近似微分方程为
在图9-2所示的坐标系中，坐标x处横截面上的弯矩为
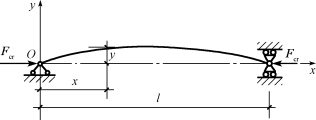
图9-2 细长杆受力情况
将式（b）代入式（a），得
进一步推导（过程从略），可得临界力为
上式即为两端铰支细长杆的临界压力计算公式，称为欧拉公式。
从欧拉公式可以看出，细长压杆的临界力Fcr与压杆的弯曲刚度成正比，而与杆长l的平方成反比。
（2）其他约束情况下细长压杆的临界力。杆端为其他约束的细长压杆，其临界力计算公式可参考前面的方法导出，也可以采用类比的方法得到。经验表明，具有相同挠曲线形状的压杆，其临界力计算公式也相同。于是，可将两端铰支约束压杆的挠曲线形状取为基本情况，而将其他杆端约束条件下压杆的挠曲线形状与之进行对比，从而得到相应杆端约束条件下压杆临界力的计算公式。为此，可将欧拉公式写成统一的形式：
(https://www.chuimin.cn)
式中μl为折算长度，表示将杆端约束条件不同的压杆计算长度l折算成两端铰支压杆的长度，μ为长度系数。几种不同杆端约束情况下的长度系数μ值列于表9-1中。从表9-1可以看出，两端铰支时，压杆在临界力作用下的挠曲线为半波正弦曲线；而一端固定另一端铰支，计算长度为l的压杆的挠曲线，其部分挠曲线（0.7l）与长为l的两端铰支的压杆的挠曲线的形状相同，因此，在这种约束条件下，折算长度为0.7l。其他约束条件下的长度系数和折算长度可以依此类推。
表9-1 压杆长度系数
【例9-1】如图9-3所示，一端固定另一端自由的细长压杆，其杆长l＝2m，截面形状为矩形，b＝20mm、h＝45mm，材料的弹性模量E＝200GPa。试计算该压杆的临界力。若把截面改为b＝h＝30mm，而保持长度不变，则该压杆的临界力又为多大？
解：（1）计算截面的惯性矩。由前述可知，该压杆必在弯曲刚度最小的xy平面内失稳，故式（9-2）的惯性矩应以最小惯性矩代入，即
（2）计算临界力。查表9-1得μ＝2，因此临界力为
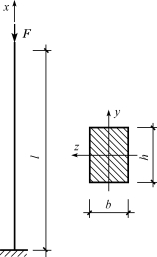
图9-3 例9-1图
（3）当截面改为b＝h＝30mm时，压杆的惯性矩为
代入欧拉公式，可得
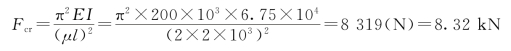
从以上两种情况分析，其横截面面积相等，支承条件也相同，但是，计算得到的临界力后者大于前者。可见在材料用量相同的条件下，选择恰当的截面形式可以提高细长压杆的临界力。
相关文章
- 详细阅读
-
力对点的矩及其计算方法详细阅读
力对点的矩是很早以前人们在使用杠杆、滑车、绞盘等机械搬运或提升重物时所形成的一个概念。若改变力的作用方向，则扳手的转动方向就会发生改变，因此，用F与d的乘积再冠以适当的正负号来表示力F使物体绕O点转动的效应，并称为力F对O点的矩，简称力矩，以符号MO表示，即O点称为转动中心，简称矩心。式中的正负号表示力矩的转向。分别计算图3-3所示的F1、F2对O点的力矩。......
2025-09-29
-
如何用改进欧拉法计算故障切除后电磁功率影响？详细阅读
应该着重指出，用改进欧拉法对故障切除后的第一个时间段的计算，与用分段计算法不同，电磁功率只用故障切除后的网络方程来求得而不必用故障切除前后的平均值。这是因为改进欧拉法的递推公式中实际已计及了故障切除前瞬间的电磁功率的影响。改进欧拉法和分段计算法的精确度是相同的。如果在输电线路始端发生两相接地短路，线路两侧开关经0.1s同时切除，试用分段计算法和改进欧拉法计算发电机的摇摆曲线，并判断系统能否保持暂态稳定。......
2025-09-29
-
打击杆结构优化方案详细阅读
图3-20 结构优化后，打击杆的应力应变分布云图与1688号节点的应力应变时间历程曲线a）应力分布云图与1688号节点的应力时间历程曲线 b）应变分布云图与1688号节点的应变时间历程曲线结构优化后，打击杆分别选用A3钢、调质45钢和调质40Cr时的寿命分布云图如图3-21所示，可见：1）结构优化后的打击杆中间部分寿命较长，原打击杆中间凸台部分的薄弱环节已经消除，这是由于结构优化后的打击杆中间部分为一整个圆柱，应力集中现象消除。......
2025-09-29
-
抓取力限制：允许的抓取力优化详细阅读
在允许的抓取力方面一般有两种观点。为了可靠地防止损坏，应根据相关的安全系数确定对这些力的限制。图3.79不同类型机械手的夹持力变化，机械手手指所能承受的最大力和力矩负载多齿型导轨机械手如图3.80所示。图3.81活塞产生的力的计算示例图3.82三种导轨技术SCHUNK机械手滑块和加工过程如图3.83所示。图3.83SCHUNK机械手滑块和加工过程图3.84显示了不同机械手手指设计选项的类型。......
2025-09-29
-
夹持力的产生及其应用详细阅读
图3.78不同力传导的三维说明对于应用中机械手最佳选择的问题并不容易回答。然而，当看到张角型机械手的夹持力变化过程与平动型机械手相比时，夹持力变化过程对于决策的相对重要性变得清晰。张角型机械手将根据手指的位置呈现不同的夹持力。相比之下，平动型机械手在整个手指行程中提供恒定的夹持力。......
2025-09-29
-
夹持力和能源的关系详细阅读
图3.86张角型机械手带有活塞的驱动结构总的来说，气动驱动在自动化技术中占有一席之地，并且在全球的大多数应用中使用。图3.87电机转速和机械手行程图3.88电动机械手闭合节拍内的行程和速度机械手传动机构也受到该控制的保护，否则不一定能实现机械手长时间的使用寿命。图3.91使用平直式电机安装的电动机械手的应用范例液压系统用于对夹持力要求特别高的应用，例如锻造部门。......
2025-09-29
-
工艺力对产品的影响详细阅读
图4.11三指机械手中工件的抛光工艺在图4.12所示的情况下，如果要从货架或底座上取下工件，则不能始终保证搬运系统定位的足够精度。图4.12从货架上取走工件补偿装置安装在机械手和搬运系统之间。图4.16FTC运动的可能性图4.17FTC传感器模块在装配阀体中的应用柔性和刚性传感器是有区别的。图4.18FTC传感器的剖视图图4.19FTC位置传感器测量原理这些传感器有不同的尺寸。......
2025-09-29
相关推荐