第二个案例是在模拟地震荷载下混凝土柱的损伤演化致失效分析。图6.38混凝土柱试样［36］图6.39试验中施加的荷载谱应用前述的损伤演化致失效的跨尺度自适应模拟与分析方法对如图6.38所示的混凝土柱试样在试验模拟的地震荷载作用下的跨尺度损伤演化过程进行模拟，模拟结果见图6.40。通过将所模拟的混凝土柱在模拟地震荷载下的损伤演化过程的数值结果与实验结果进行对比，表明数值模拟结果与实验结果吻合较好，表明所发展的算法是可靠的。......
2023-08-26
地震荷载下钢材损伤演化率与本构关系分析
【摘要】：在极端荷载作用下，钢结构中处于高应力区的连接节点会发生塑性变形同时伴以损伤演化。对于这类塑性损伤问题，Lemaitre损伤演化律可用于描述地震荷载下的塑性损伤行为和损伤动力学本构关系。损伤耗散势函数可以表示为：其中S是与损伤耗能强度相关的材料常数。塑性损伤演化的结果导致材料性能劣化，材料损伤后的本构关系亦随损伤演化而改变。因此，损伤后材料本构关系须由方程和方程决定的塑性损伤耗散势与塑性本构关系耦合而成。
在极端荷载作用下，钢结构中处于高应力区的连接节点会发生塑性变形同时伴以损伤演化。对于这类塑性损伤问题，Lemaitre损伤演化律可用于描述地震荷载下的塑性损伤行为和损伤动力学本构关系。塑性损伤演化过程中损伤变量D的演化规律可以写成损伤耗散势函数FD对损伤耗能率的偏导数：
其中p是累积塑性应变，Y是损伤耗能率（与损伤变量D对偶的广义力）
其中σeq为Von Mises等效应力
；Rv是三轴应力函数，可表示为
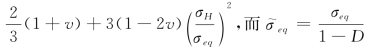是损伤后的等效应力。
损伤耗散势函数可以表示为：
其中S是与损伤耗能强度相关的材料常数。将方程（4－97）～（4－99）联立即可得损伤演化方程。
在损伤耗散势函数中引入Von Mises屈服函数和混合塑性硬化模式，并使其与塑性屈服面重合，则有：
其中
是偏应力张量，
是背应力张量，σy＋R是考虑各向同性硬化后的随动屈服应力。
塑性损伤演化的结果导致材料性能劣化，材料损伤后的本构关系亦随损伤演化而改变。因此，损伤后材料本构关系须由方程（4－99）和方程（4－100）决定的塑性损伤耗散势与塑性本构关系耦合而成。基于上述表达式，钢材中发生各向同性延性损伤后的本构关系可以总结如下：
1.损伤本构方程
应力和应变张量：
弹性损伤本构关系：
塑性损伤本构关系：
2.损伤演化率
局部失效的临界条件为：D＝Dc，其中
，即此时细观尺度上的体元发生破坏。
有关结构损伤多尺度模拟与分析的文章
- 详细阅读
-
基于Chapman-Enskog法的颗粒相本详细阅读
在稠密气体分子运动的动理学理论 的分析方法中，主要有Chapman-Enskog迭代法和Grad的13矩方法。首先从Chapman-Enskog法来考察颗粒相脉动量的本构关系，由于问题的复杂性，仅探讨了颗粒近乎弹性 的情形，并与现有的近乎弹性的快速颗粒流理论成果作比较。......
2023-06-22
-
结构损伤多尺度模拟与分析：混凝土损伤特征与演详细阅读
构件受力后，钢筋和混凝土之间有相对滑移趋势时，产生摩阻力。这个过程就是钢筋混凝土粘结界面的损伤演化过程。现行钢混结构设计理论大多是基于平截面假定进行的，这隐含着钢筋和混凝土这两种性质截然不同的材料粘结良好，以确保二者变形协调。保障钢筋和混凝土的粘结良好是确保钢混结构安全的重要条件之一。图2.44钢筋与混凝土粘结失效引发的结构破坏......
2023-08-26
-
颗粒流本构关系的探讨详细阅读
采用分子混沌假设，并认为颗粒之间以二体碰撞为主。上述本构关系式由Gidaspow 针对气固两相流率先提出，在气固两相流模拟中获得了较广泛的应用。因此，上述本构关系严格地说，仅适用于速度梯度较小、颗粒近乎弹性的颗粒流。......
2023-06-22
- 详细阅读
-
材料本构关系与流动应力实验的理论基础详细阅读
为了较真实地模拟材料的切削过程，应把材料的流动应力视为应变、应变率和温度的函数关系，表示为：。表2-1 工件化学成分 描述材料流动应力的模型通常有多种形式。Johnson-Cook本构关系形式简单、待定系数少、适应性强，是应用最为广泛的一种模型[103]。使用较多的流动应力实验方法主要有Hopkinson高速冲击法[104]和正交槽铣法[105]。根据上述情况和国内实验资源，拟采用Hopkinson高速冲击法进行测试，以获取材料的JC本构模型。......
2023-06-27
-
混凝土损伤演化跨尺度自适应分析详细阅读
在建立了混凝土损伤跨尺度演化过程的自适应模拟方法以后，要实现损伤跨尺度演化过程自适应分析，还需要建立其有限元分析基本方程组。因为在Ωmacro中混凝土处于线弹性阶段，所以可以表示为：其中为连接子区域Ωmacro与Ωtrans的拉格朗日乘子为连接子区域Ωtrans与Ωmeso的拉格朗日乘子。基于损伤力学的有效应力概念，有效应力张量表示为：由此可得到：为便于有限元程序实施，需要将方程～离散化，组装成有限元基本方程组。......
2023-08-26
-
混凝土损伤特性与演化规律详细阅读
从材料层次上看，混凝土类脆性固体材料属于先天性微裂纹材料，材料中大量存在的先天微裂纹是这类材料及其组成的结构在服役过程中损伤演化导致材料或结构破坏的源头。细观尺度上混凝土的观测结果表明，非均匀性和先天存在的细观裂纹是混凝土材料最重要的材料特性，而内部存在的微裂纹对混凝土这类脆性材料的损伤性能及其破坏起到了至关重要的作用。......
2023-08-26
相关推荐