首页理论教育无侧移结构的位移法计算与弯矩图绘制

无侧移结构的位移法计算与弯矩图绘制

2025-09-29 理论教育版权反馈

【摘要】：只有结点角位移而无结点线位移的结构称为无侧移结构。因为只有角位移，只需建立刚结点的力矩平衡方程就可以求解出基本未知量，进而计算杆端弯矩绘制内力图。用位移法计算图15-8所示刚架，并作其弯矩图。对于具有多个结点角位移未知量的结构，可利用每个刚性结点列出一个力矩平衡方程，由于刚性结点的数目与结点角位移的数目是相同的，则所列出的位移法方程的个数与基本未知量的个数恰好相等，解联立方程即可求解出所有的基本未知量。

只有结点角位移而无结点线位移的结构称为无侧移结构。连续梁和无侧移刚架就属于此类结构。因为只有角位移，只需建立刚结点的力矩平衡方程就可以求解出基本未知量，进而计算杆端弯矩绘制内力图。

【例15-1】用位移法作连续梁的弯矩图，如图15-7（a）所示。已知，各杆刚度EI为常数。

解：（1）确定基本未知量。连续梁只有一个刚结点B，基本未知量为B结点的角位移θB。

（2）将连续梁拆成两个单跨超静定梁，如图15-7（b）所示。

（3）利用等截面直杆的刚度方程，列出各杆件的杆端弯矩方程（两杆的线刚度相等）：

pagenumber_ebook=208,pagenumber_book=199

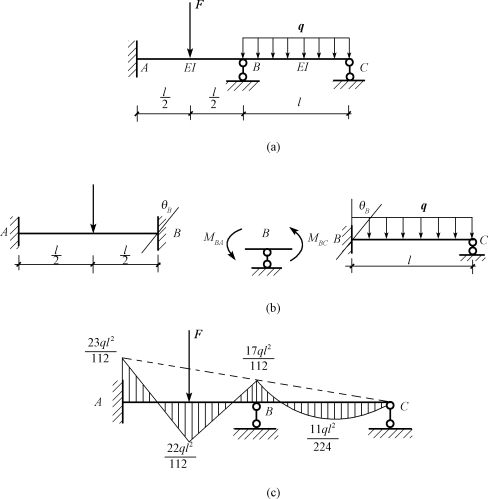
pagenumber_ebook=209,pagenumber_book=200

图15-7　例15-1图

pagenumber_ebook=209,pagenumber_book=200

（4）建立位移法方程，求解基本未知量。取刚性结点B为隔离体，如图15-7（b）所示，由力矩平衡方程可得

∑MB＝0,MBA＋MBC＝0

即

从而求得

（5）代回转角位移方程，求出各杆的杆端弯矩：

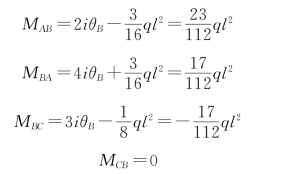
pagenumber_ebook=209,pagenumber_book=200

（6）绘制弯矩图，如图15-7（c）所示。

【例15-2】用位移法计算图15-8（a）所示刚架，并作其弯矩图。设各杆EI为常数。(https://www.chuimin.cn)

pagenumber_ebook=210,pagenumber_book=201

图15-8　例15-2图

解：（1）确定基本未知量。基本未知量为B结点的角位移φB。

（2）利用等截面直杆的刚度方程，列出各杆件的杆端弯矩方程。为了计算方便，各杆线刚度取相对值，可设则

pagenumber_ebook=210,pagenumber_book=201

查表14-1并利用叠加原理，可得到各杆件的杆端弯矩方程为

pagenumber_ebook=210,pagenumber_book=201

（3）建立位移法方程，求解基本未知量。取刚性结点B为隔离体，如图15-8（b）所示，由力矩平衡方程可得

∑MB＝0,MBA＋MBC＋MBD＝0

即

9iφB＋60＋8iφB－75＋12iφB＝0

解得

（4）计算各杆件的杆端弯矩。将所得结果代入杆端弯矩方程中可得

pagenumber_ebook=210,pagenumber_book=201

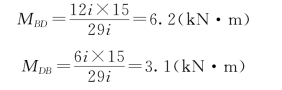
pagenumber_ebook=211,pagenumber_book=202

（5）绘制弯矩图。根据所计算的各杆杆端弯矩值和荷载情况，应用叠加法作弯矩图的方法，可直接绘出各杆的弯矩图，如图15-8（c）所示。

对于具有多个结点角位移未知量的结构，可利用每个刚性结点列出一个力矩平衡方程，由于刚性结点的数目与结点角位移的数目是相同的，则所列出的位移法方程的个数与基本未知量的个数恰好相等，解联立方程即可求解出所有的基本未知量。然后代入杆端弯矩方程中即可求解出各杆的杆端弯矩值，如上例，便可作出内力图。