根据上述力法原理，用力法计算超静定结构内力的计算步骤如下：去掉原结构的多余约束并代之以多余未知力，选取基本体系。试用力法计算图15-12所示超静定梁的内力，并绘制出弯矩图。由基本体系在多余未知力X1及荷载的共同作用下，B点处沿X1方向上的位移等于零的变形条件，建立力法方程为计算方程中的系数和自由项。因此，它的弯矩图与同跨度、同荷载的简支梁相比较，最大弯矩峰值较小，使整个梁上内力分布得以改善。......
2025-09-30
用位移法计算连续梁与超静定刚架
【摘要】：位移法计算连续梁及超静定刚架一般步骤如下：确定基本未知量和基本结构。用位移法计算时，只有节点转角基本未知量，故仅需建立刚节点处的力矩平衡方程，即可求解出全部未知量，进而计算杆端弯矩，绘制出内力图。此连续梁只有一个刚节点B的转角位移θB，如图15-32所示。列各杆杆端弯矩计算式。用位移法计算图15-34所示的超静定刚架，并作出弯矩图。
位移法计算连续梁及超静定刚架一般步骤如下：
（1）确定基本未知量和基本结构。
（2）列出各杆端转角位移方程。
（3）根据平衡条件建立位移法基本方程（一般对有转角位移的刚节点取力矩平衡方程，有节点线位移时则考虑线位移方向的静力平衡方程）。
（4）解出未知量。
（5）求出杆端内力。
（6）作出内力图。
1.无节点线位移结构的计算
如果结构的各节点只有转角而没有线位移，则为无节点线位移结构。用位移法计算时，只有节点转角基本未知量，故仅需建立刚节点处的力矩平衡方程，即可求解出全部未知量，进而计算杆端弯矩，绘制出内力图。下面举例说明具体计算过程。
【例15-6】 用位移法计算图15-32（a）所示的连续梁，作出内力图，P＝
ql（刚度EI为常数）。
【解】 （1）确定基本未知量。此连续梁只有一个刚节点B的转角位移θB，如图15-32（b）所示。
（2）写出转角位移方程：
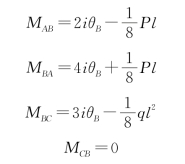
（3）对刚节点B取力矩平衡：
（4）解得：θB＝－
（负号说明θB逆时针转）
（5）将θB＝－
代入转角位移方程计算出各杆端弯矩[图15-32（d）、（e）]：
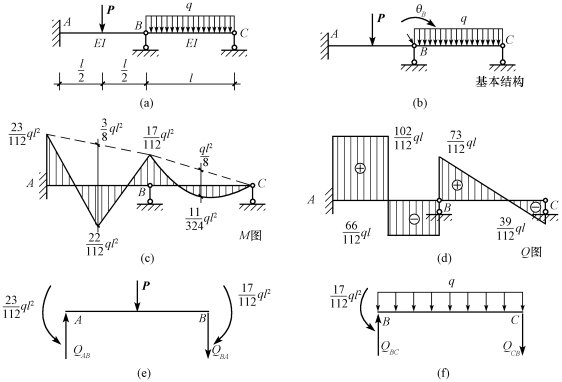
图15-32
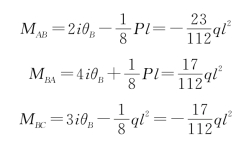
（6）作出弯矩图和剪力图，如图15-32（c）、（d）所示。
【例15-7】 作图15-33（a）所示刚架的弯矩图。
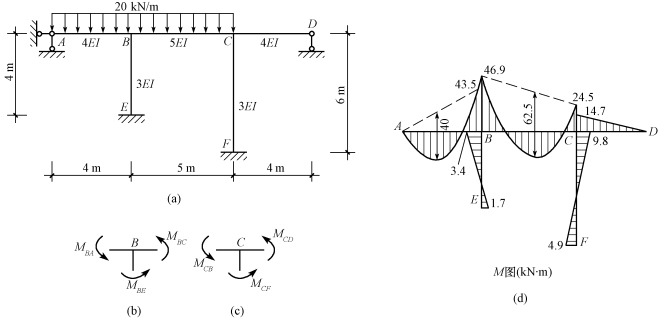
图15-33
【解】 （1）基本未知量为刚节点B、C的转角θB、θC。
（2）列各杆杆端弯矩计算式。设EI＝1，各杆线刚度为
（3）建立位移法基本方程求解基本未知量。
节点B，如图15-33（b）所示：
(https://www.chuimin.cn)
节点C，如图15-33（c）所示：
杆端弯矩代入后：
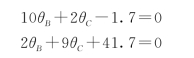
联立求解得：
（4）计算杆端弯矩：
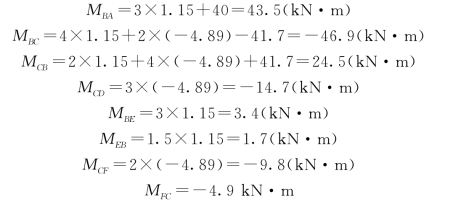
（5）作弯矩图如图15-33（d）所示。
2.有节点线位移刚架的计算
如果结构的节点有线位移，则此结构称为有节点线位移结构。对于有节点线位移的刚架来说，一般要考虑杆端剪力，建立线位移方向的静力平衡方程和刚节点处的力矩平衡方程，才能解出未知量，下面举例说明。
【例15-8】 用位移法计算图15-34（a）所示的超静定刚架，并作出弯矩图。
【解】 （1）确定基本未知量。此刚架有一个刚节点C转角位移θ，一个线位移Δ，如图15-34（b）所示。
（2）列出转角位移方程。
图15-34
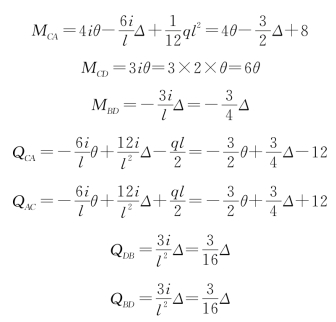
（3）对刚节点C取力矩平衡，如图15-34（c）所示。
取整体结构水平合力投影方程，如图15-34（c）所示。
代入杆端转角位移方程化简得：
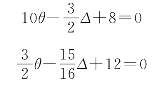
（4）联立解得：
（5）将θ、Δ代入转角位移方程求出各杆端弯矩：
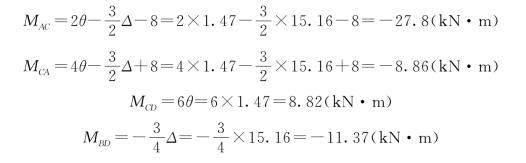
（6）作出弯矩图如图15-34（d）所示。
相关文章
- 详细阅读
-
基本概念与思路：位移法解决超静定结构的方法详细阅读
力法是以多余未知力为基本未知量，位移法则是以某些结点的位移作为基本未知量，这是力法和位移法的基本区别之一。为了说明位移法的基本概念，现以图15-1所示超静定刚架为例来分析其位移。综上所述，位移法的基本思路是：分析结构的结点位移情况，确定基本未知量。利用平衡条件建立位移法基本方程，求解基本未知量。......
2025-09-29
-
静定平面刚架内力计算方法详细阅读
静定平面刚架的内力计算同梁一样，仍是用截面法截取隔离体，然后用平衡条件求解。根据荷载情况，将刚架分解成若干杆段，由平衡条件求出杆端内力。该杆上作用有一集中荷载，可以分为CE和EB两个无荷载区段，用截面法求出下列控制截面的弯矩：便可以绘制出该杆弯矩图。根据荷载和已经求出的反力，可以用截面法求出杆件各个控制截面的剪力和轴力，从而绘制出整个钢架的剪力图和轴力图，如图12-18、所示。......
2025-09-29
-
用力矩分配法计算连续梁和无侧移刚架设计技巧详细阅读
上节用只有一个刚结点的结构介绍了力矩分配法的基本概念。对于具有两个以上刚结点的结构也可用力矩分配法进行计算。多结点力矩分配法的计算步骤如下：求出汇交于各结点每一杆端的力矩分配系数μij，并确定其传递系数Cij。固定刚结点B和C，各杆的固端弯矩为其余各固端弯矩均为零。刚结点B的约束力矩除固端弯矩外，还包括传递过来的传递弯矩，即所以传递弯矩为进行第二轮计算。用力矩分配法作图16-8所示刚架的弯矩图。......
2025-09-29
-
梁的计算简图与静定基本形式详细阅读
固定铰支座限制支承处沿任何方向的线位移，因此，相应支座反力可用两个分力表示，例如水平反力与垂直反力。一端或两端向外伸出的简支梁，称为外伸梁。以上三种梁的支座反力只有三个，可由静力平衡方程完全确定。这类仅用平衡方程即可求出全部未知反力的梁称为静定梁。图7-8梁的基本形式......
2025-09-29
-
静定平面刚架内力计算方法(建筑力学第3版)详细阅读
静定平面刚架的内力包括弯矩、剪力与轴力。根据前述内力图绘制法逐杆绘制刚架的内力图，并进行校核。求支座反力时要根据支座的性质定出支座反力未知量的个数，然后假定反力方向，由平衡方程确定其数值。求图13-9所示刚架的支座反力。（二）刚架杆截面内力的计算1.刚架内力正负号的规定刚架的内力有弯矩、剪力和轴力。如杆端截面C1、C2的弯矩分别用MCA、MCD表示，剪力和轴力分别用QCA、QCD和NCA、NCD表示。......
2025-09-30
-
无侧移结构的位移法计算与弯矩图绘制详细阅读
只有结点角位移而无结点线位移的结构称为无侧移结构。因为只有角位移，只需建立刚结点的力矩平衡方程就可以求解出基本未知量，进而计算杆端弯矩绘制内力图。用位移法计算图15-8所示刚架，并作其弯矩图。对于具有多个结点角位移未知量的结构，可利用每个刚性结点列出一个力矩平衡方程，由于刚性结点的数目与结点角位移的数目是相同的，则所列出的位移法方程的个数与基本未知量的个数恰好相等，解联立方程即可求解出所有的基本未知量。......
2025-09-29
-
应用图乘法计算静定结构位移的优化方法详细阅读
图乘法计算位移的解题步骤：画出结构在实际荷载作用下的弯矩图MP；根据所求位移选定相应的虚拟状态，画出单位弯矩图图；分段计算一个弯矩图的面积A及其形心所对应的另外一个弯矩图的竖标yC；将A、yC代入图乘公式计算所求位移。但因图形对称，可计算一半再乘以2。所以求图13-17所示外伸梁C点的竖向位移ΔCV。各杆的EI为常数。在应用图乘法时，把单位力产生的图作为图形的面积A，其中梁上的图面积作为A1，柱上的图面积作为A2。......
2025-09-29
相关推荐