、An彼此独立,则称之为独立事件群。6.完全事件系如果多个事件A1、A2、A3、…试验的全部结果包含n个基本事件,事件A包含其中m1个基本事件,事件B包含其中m2个基本事件。定理:事件A和事件B为独立事件,则事件A与事件B同时发生的概率为各自概率的乘积,则:推理:A1、A2、…......
2025-09-30
直线回归是回归分析中最简单的一种,又称为简单回归。
(一)直线回归方程
散点图上呈现直线趋势的两个变数,自变量x的每一个取值都有y的一个分布与之对应。在这种情况下,可以利用直线回归方程描述两个变数之间的关系:
![]()
其中x是自变量;![]() 是和x的两相对应的点估计值;a是x=0时的
是和x的两相对应的点估计值;a是x=0时的![]() 值,即回归直线在y轴上的截距,叫回归截距;b是x每增加一个单位时,
值,即回归直线在y轴上的截距,叫回归截距;b是x每增加一个单位时,![]() 平均地将要增加或减少的单位数,叫回归系数。
平均地将要增加或减少的单位数,叫回归系数。
使得![]() =a+bx最好地代表y和x在数量上的互变关系,根据最小二乘法:
=a+bx最好地代表y和x在数量上的互变关系,根据最小二乘法:
![]()
因此,分别对a和b求偏导数并令其为0,即可得到正规方程组

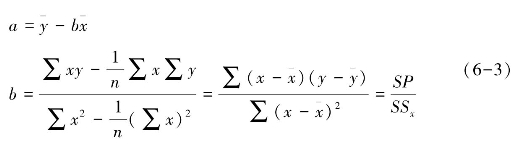
分子![]() 是x的离均差和y的离均差的乘积之和,简称乘积和(sum ofproducts),记作SP;分母是x的离均差平方和,记作SSx。将(6-2)式、(6-3)式算得的a和b值代入(6-1),即可保证
是x的离均差和y的离均差的乘积之和,简称乘积和(sum ofproducts),记作SP;分母是x的离均差平方和,记作SSx。将(6-2)式、(6-3)式算得的a和b值代入(6-1),即可保证![]() 为最小,同时使∑(y-
为最小,同时使∑(y-![]() )=0。
)=0。
a和b值皆可正可负,随具体资料而异。当a>0时,表示回归直线在I、II象限交于y轴;当a<0时,表示回归直线在Ⅲ、V象限交于y轴;当b>0时,表示y随x的增大而增大;当b<0时,表示y随x的増大而减小。若b=0或和0的差异不显著,则表明y的变异和x的取值大小无关,直线回归关系不能成立。
以上是a和b值的统计学解释。在具体问题中,a和b值将有专业上的实际意义。
将(6-2)式代入(6-1)式可得:
![]()
由(6-4)式可见,当x=![]() 时,必有
时,必有![]() ,所以回归直线一定通过
,所以回归直线一定通过![]() 坐标点。记住这一特性,有助于绘制具体资料的回归直线。
坐标点。记住这一特性,有助于绘制具体资料的回归直线。
由(6-4)式还可看出:①当x以离均差![]() 为单位时,回归直线的位置仅决定于
为单位时,回归直线的位置仅决定于![]() 和b;②当将坐标轴平移到以
和b;②当将坐标轴平移到以![]() 为原点时,回归直线的走向仅决定于b,所以一般又称b为回归斜率(regression slope)
为原点时,回归直线的走向仅决定于b,所以一般又称b为回归斜率(regression slope)
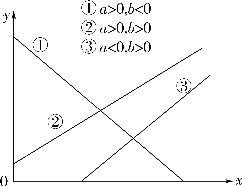
图6-1 直线回归方程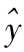 =a+bx的图
=a+bx的图
(二)直线回归方程的计算
以一个实例说明回归统计数计算的过程。
[例1]一些夏季害虫盛发期的早迟和春季温度高低有关。江苏武进连续9年测定3月下旬至4月中旬旬平均温度累积值(x,旬·度)和水稻一代三化螟盛发期(y,以5月10日为0)的关系,得结果于表6-1。试计算其直线回归方程。
表6-1 累积温和一代三化螟盛发期的关系
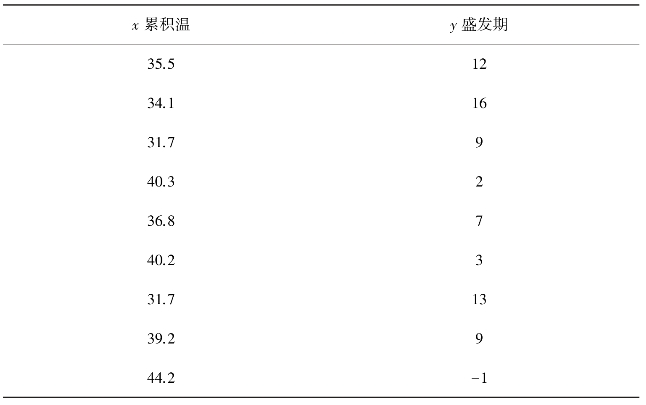
首先由表6-1算得回归分析所必需的6个一级数据(即由观察值直接算得的数据),
n=9
∑x=35.5+34.1+...+44.2=333.7
∑x2=35.52+34.12+...+44.22=12 517.49
∑y=12+16+...+(-1)=70
∗∑y2=122+162+...+(-1)2=794
∑xy=(35.5×12)+(34.1×16)+...+[44.2×(-1)]=2 346.4然后,由一级数据算得5个二级数据:
SSx=∑x2-(∑x)2/n=12 517.49-(333.7)2/9=144.635 6
∗SSy=∑y2-(∑y)2/n=794-(70)2/9=249.555 6(https://www.chuimin.cn)
SP=∑xy-∑x∑y/n=2436.4-(333.7X70)/9=-159.044 4
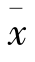 =∑x/n=333.7/9=37.077 8
=∑x/n=333.7/9=37.077 8
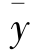 =∑y/n=70/9=7.777 8
=∑y/n=70/9=7.777 8
因而有:b=SP/SSx=-159.044 4/144.635 6=-1.099 6[天/(旬·度)]
a=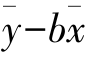 =7.777 8-(-1.099 6×37.077 8)=48.548 5(天)
=7.777 8-(-1.099 6×37.077 8)=48.548 5(天)
故得到表6-1资料的回归方程: =48.548 5-1.099 6x或化简成:
=48.548 5-1.099 6x或化简成: =48.5-1.1x
=48.5-1.1x
(三)直线回归方程的图示
直线回归图包括回归直线的图象和散点图,它可以醒目地表示x和y的数量关系。
制作直线回归图时,首先以x为横坐标,以y为纵坐标构建直角坐标系(纵、横坐标皆需标明名称和单位);然后取x坐标上的一个小值x1代入回归方程得![]() ,取一个大值x2代入回归方程得
,取一个大值x2代入回归方程得![]() ,连接坐标点(x1,
,连接坐标点(x1,![]() )和(x2,
)和(x2,![]() )即成一条回归直线。如例6-1资料,以x1=31.7代入回归方程得
)即成一条回归直线。如例6-1资料,以x1=31.7代入回归方程得![]() =13.69;以x2=44.2代入回归方程得
=13.69;以x2=44.2代入回归方程得![]() =-0.05。在图6-2上确定(31.7,13.69)和(44.2,-0.05)这两个点,再连接之,即为
=-0.05。在图6-2上确定(31.7,13.69)和(44.2,-0.05)这两个点,再连接之,即为![]() =48.5485-1.099 6x的直线图象。注意:此直线必通过点
=48.5485-1.099 6x的直线图象。注意:此直线必通过点![]() ,它可作为制图是否正确的核对。最后,将实测的各对(xi,yi)数值也用坐标点标于图6-2上。
,它可作为制图是否正确的核对。最后,将实测的各对(xi,yi)数值也用坐标点标于图6-2上。
图6-2的回归直线是9个观察坐标点的代表,它不仅表示了表6-1资料的基本趋势,也便于预测。如某年3月下旬至4月中旬的积温为40旬·度,则在图6-2上可查到一代三化螟盛发期的点估计值在5月14日-15日,这和将x=40代人原方程得到![]() =48.548 5-(1.099 6×40)=4.6是一致的。因为回归直线是综合9年结果而得出的一般趋势,所以其代表性比任何一个实际的坐标点都好。
=48.548 5-(1.099 6×40)=4.6是一致的。因为回归直线是综合9年结果而得出的一般趋势,所以其代表性比任何一个实际的坐标点都好。
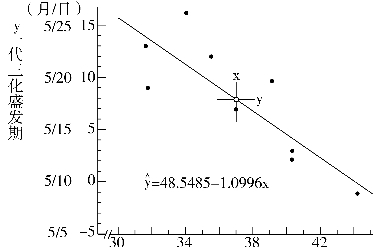
图6-2 旬平均温度累积值和一代三化螟盛发期的关系
(四)直线回归的估计标准误
由图6-2可见,满足Q=∑(y-![]() )2为最小的直线回归方程和实测的观察点并不重合,表明该回归方程仍然存在随机误差。Q就是误差的一种度代三化螟盛发期的关系量,称之为离回归平方和(sum of squares due to deviation from regres⁃sion)或剩余平方和。由于在建立回归方程时用了a和b两个统计数,故Q的自由度v=n-2。因而,可定义回归方程的估计标准误Sy/x为:
)2为最小的直线回归方程和实测的观察点并不重合,表明该回归方程仍然存在随机误差。Q就是误差的一种度代三化螟盛发期的关系量,称之为离回归平方和(sum of squares due to deviation from regres⁃sion)或剩余平方和。由于在建立回归方程时用了a和b两个统计数,故Q的自由度v=n-2。因而,可定义回归方程的估计标准误Sy/x为:
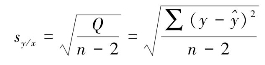
若各个观察点愈靠近回归线,将愈小(极端地说,当各观察点都落在回归线上时,若各观察点在回归线上下分散得愈远,则Sy/x愈大。故样本的Sy/x是回归精确度的度量,Sy/x愈小,由回归方程估计y的精确性愈高。
计算Sy/x的主要手续在于求Q。直接计算不仅步骤多、工作量大,而且若数字保留位数不够,会引起较大的计算误差。为简化手续,可从以下恒等式得出:

(五)直线回归的数学模型和基本假定
回归分析的依据是直线回归模型。在这一模型中,Y总体的每一个值由以下三部分组成:回归截距α;回归系数β;Y变数的随机误差ε。因此,总体直线回归的数学模型可表示为:
![]()
其中εj~N(0,![]() )。相应的样本线性组成为:
)。相应的样本线性组成为:
![]()
在按上述模型进行回归分析时,假定:
(1)Y变数是随机变数,而X变数则是没有误差的固定变数,至少和Y变数比较起来X的误差小到可以忽略。
(2)在任一X上都存在着一个Y总体(可称为条件总体),它是作正态分布的,其平均数μY/X是X的线性函数:
![]()
μY/X的样本估计值 ,
,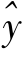 与X的关系就是线性回归方程(6-1)式。
与X的关系就是线性回归方程(6-1)式。
(3)所有的Y总体都具有共同的方差![]() ,这一方差不因X的不同而不同,而直线回归总体具有N(α+βX,
,这一方差不因X的不同而不同,而直线回归总体具有N(α+βX,![]() )。试验所得的一组观察值(xi,yi)只是N(α+βX,
)。试验所得的一组观察值(xi,yi)只是N(α+βX,![]() )中的一个随机样本。
)中的一个随机样本。
(4)随机误差ε相互独立,并作正态分布,具有N(0,![]() )。
)。
因此,模型中的参数共有a,即直线的截距;β,即直线的斜率;![]() ,误差的方差。其样本的相应估计值为a、b和
,误差的方差。其样本的相应估计值为a、b和![]()
理解上述模型和假定,有助于正确地进行回归分析。
相关文章

、An彼此独立,则称之为独立事件群。6.完全事件系如果多个事件A1、A2、A3、…试验的全部结果包含n个基本事件,事件A包含其中m1个基本事件,事件B包含其中m2个基本事件。定理:事件A和事件B为独立事件,则事件A与事件B同时发生的概率为各自概率的乘积,则:推理:A1、A2、…......
2025-09-30

样本平均数的分布与其他分布一样,有两个重要参数,一个是样本平均数的平均数,记作μ,另一个是样本平均数的方差,记作。标准误大,各样本平均数间差异程度大,样本平均数的精确性低。从某特定总体抽样,因为σ是一定值,所以只有增大样本容量,才能降低样本平均数的抽样误差。......
2025-09-30

试验结果只能是“非此即彼”构成对立事件,将这种事件构成的总体称为二项总体,其概率分布称为二项分布。显然,二项分布是一种离散型随机变量的概率分布。此外,还有不少随机变量的概率分布在一定条件下以正态分布为其极限分布。关于正态分布的概率计算,我们先从标准正态分布着手。......
2025-09-30

为了研究随机现象,需要进行大量重复的调查、试验、测试等,这些统称为试验。频率表明了事件频繁出现的程度,因而其稳定性说明了随机事件发生的可能性大小,是其本身固有的客观属性,提示了隐藏在随机现象中的规律性。在一般情况下,随机事件的概率P是不可能准确得到的。通常以试验次数n充分大时,随机事件A的频率作为该随机事件概率的近似值。......
2025-09-30

常用希腊字母表示,例如用μ表示总体平均数,用σ表示总体标准差等。实际上,统计学关心的是总体参数的大小,其依据是统计量及其性质。为了便于处理实际问题,统计学中常用若干典型的分布模式来近似的描写实际资料,如正态分布、二项分布和泊松分布等,常称为统计模型。利用统计模型进行统计分析可以简化运算。......
2025-09-30

为了获得这些软弱结构面的抗渗强度,中国电建集团中南勘测设计研究院有限公司采用多种试验方法进行了试验研究,经综合分析后得到的软弱结构面抗渗强度指标为:坝基岩体层间夹层的临界水力梯度为5.35,破坏水力梯度为33.79;挤压破碎带临界水力梯度为15.91,破坏水力梯度为48.66。因此,从工程安全及经济性角度综合出发,左非3坝基软弱夹层抗渗透变形破坏的水力梯度确定为30.0。......
2025-09-29

两直线的相对位置有以下三种:平行、相交、交叉。图2-43求相交两直线的投影已知图;作图解:根据相交直线的投影特点,可定出交点的V投影,利用交点可求出直线CD的V 投影。......
2025-09-29

为了准确地表示样本内各个观测值的变异程度,首先会考虑到以平均数为标准,求出各个观测值与平均数的离差,即,称为离均差。统计学上把样本方差S2的平方根叫作样本标准差,记为S,即:所以(3-3)式可改写为:相应的总体参数叫总体标准差,记为σ。......
2025-09-30
相关推荐