直线回归是回归分析中最简单的一种，又称为简单回归。（一）直线回归方程散点图上呈现直线趋势的两个变数，自变量x的每一个取值都有y的一个分布与之对应。试计算其直线回归方程。为简化手续，可从以下恒等式得出：（五）直线回归的数学模型和基本假定回归分析的依据是直线回归模型。......
2023-11-17
SPSS数据分析法-生态数据分析与建模
【摘要】：表15-2数据视图中各类型的设定3．进行单因素方差分析。图15-6数据统计分析结果输出4．接下来再看方差齐性检验的结果。来自正态总体的两个样本进行均值比较常使用T检验的方法。同样是数据输入完成后，依次点击“分析—比较均值—独立样本T检验”。
一、方差分析
（一）方差分析的步骤
1．数据输入。以表15-1为例，第一列6组不同数字代表6个不同处理，相同数字代表同一处理下3个重复，从第二列开始即为需要分析的不同指标。
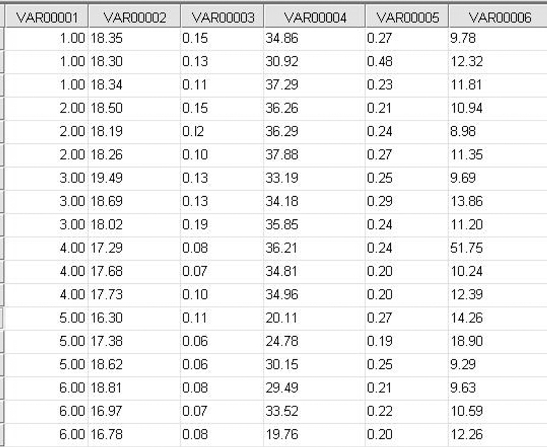
表15-1 数据输入表
2．选择左下角“变量视图”修改数据格式见图15-2。
图15-1 变量视图位置图
如表15-2，可以进行名称、类型、宽度、小数位数、标签等的设定。
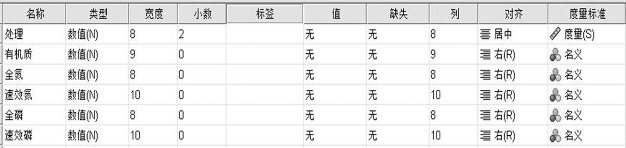
表15-2 数据视图中各类型的设定
3．进行单因素方差分析。
在菜单栏中点击“分析—比较均值—单因素ANOVA”。
图15-2 单因素ANOVA的分析路径
在弹出的对话框中，将处理作为因子，各测量指标作为因变量，选中导入右边对应位置见图15-3，然后进行两两比较。
图15-3 单因素ANOVA自变量和应变量的选择
说明：自变量（F）为处理，因变量（E）分别为：有机质、全氮、速效氮、全磷、速效磷在图15-5的界面右侧选择“两两比较”按钮，弹出如图15-4所示界面：假定方差齐性，常用方法为LSD和Duncan；未假定方差齐性，常用方法为Tamhane’s T2（M）和Dunnett’s T3（3），选择完成，点击继续按钮。
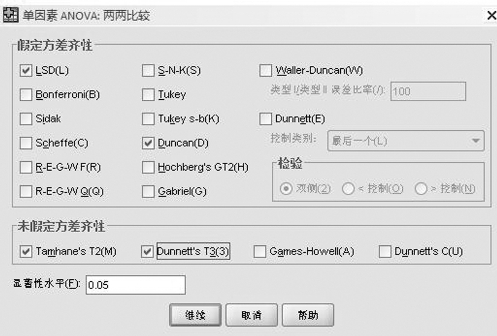
图15-4 双重比较的选项卡
然后在图15-3界面右侧点击“选项”按钮，进入选项对话框见图15-5，一般只需选择描述性和方差同质性检验，来检验所用的两两比较的方法是否适用，点击继续，最后点击确定，即查看单因素（ANOVA）方差分析的结果。
图15-5 单因素ANOVA分析界面中选择“选项”按钮后的对话框
结果中，先看描述性统计量，从下图15-6表格中可以看出每个处理的均值、标准差、标准误、极大值、极小值等。可以将表格进行剪切，粘贴到Excel表格中进行进一步的处理，一般用到的数据是“平均值和标准差”（图中框起来的部分），得到“平均值±标准差”的格式制成表格。
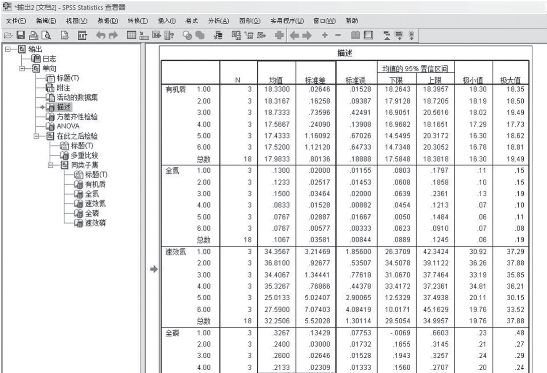
图15-6 数据统计分析结果输出
4．接下来再看方差齐性检验的结果。
当显著性那一列的对应指标值大于0．05时，即为方差齐性，就可以继续往下看LSD分析（多重比较）的结果，当显著性的值小于0．05时，即为方差非齐性，就需要对分析的数据进行进一步的处理了，比如取对数等。
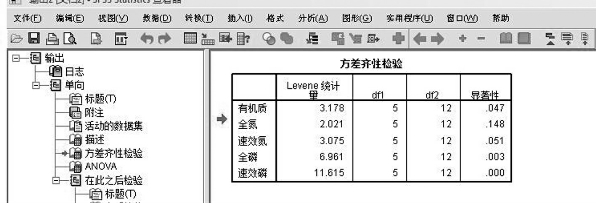
图15-7 方差齐性检验分析
对LSD分析的结果，可以通过均值差这一列看是否有“∗”来判断各处理间是否具有显著性的差异；同样，也可以按显著性那一列，若显著性的值小于0．05，说明他们之间差异显著，反之不显著。如表15-3，以全氮为例。
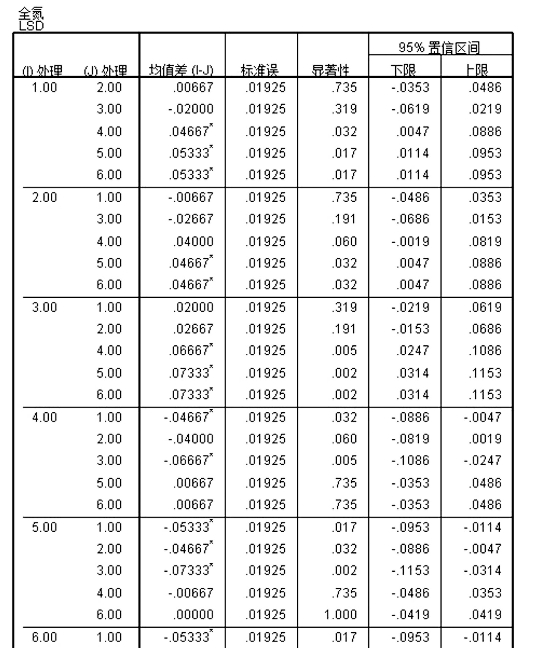
表15-3 以LSD分析的结果判断各处理之间的差异显著性（截图）
二、差异显著性字母标记
1．将描述性统计结果中各处理的平均值按照从大到小进行排序，在平均值最大的平均数上标字母a。
2．再将该平均值依次和其以下的各平均数相比，若差异不显著，则标相同字母a，直到出现与之相比差异显著的平均数为止，并在出现显著差异的数字上标字母b。
3．接着以标有b的平均值为标准，与除了平均值最大的平均数以外，按平均数按从大到小的顺序继续比，凡差异不显著的继续标b，直到出现显著性差异停止，并标上字母c。
4．一直重复上述操作，直到最小平均数都有了字母标记为止。
三、相关性分析
1．将各数据的指标按列放置，之后在菜单栏中点“分析—相关—双变量”。
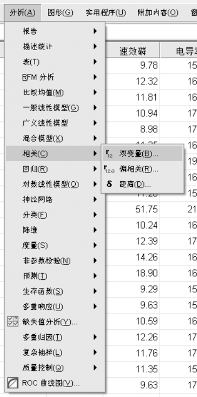
图15-8 相关分析选项卡(www.chuimin.cn)
2．弹出如下对话框（图15-9），将要进行相关性分析的指标导入右边的变量框中，点击“选项”，选择均值和标准差，再点击“继续”。在相关系数中选择Pearson或者Spearman都可以，进行显著性双侧检验，标记显著性相关前打勾，最后点击确定。
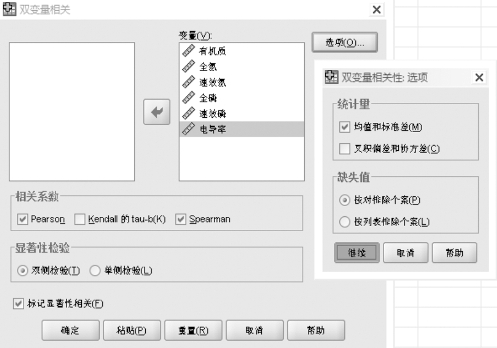
图15-9 双变量相关性分析选项卡
3．得到如下的相关性分析的表格见表15-3。
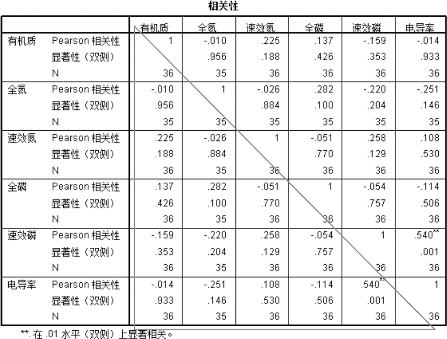
表15-3 Pearson相关性极显著性分析报表输出
4．将表格剪切后再粘贴到Excel中见表15-4，去掉不必要的数据，即可得到如下表格，见表15-5，此表格为表的学术论文中相关性表达的常见格式。
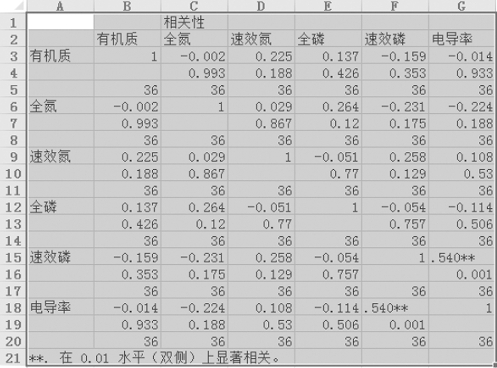
表15-4 表格剪切后再粘贴到Excel
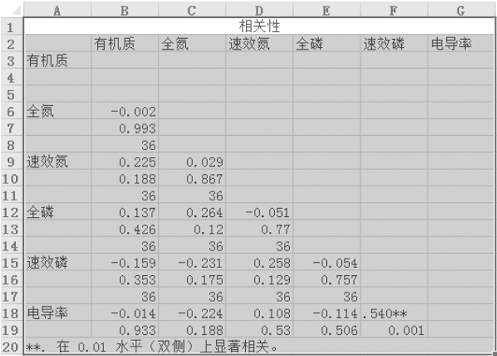
表15-5 相关性和显著性总表
四、回归分析
同样是数据输入完成后，依次点击“分析—回归—线性”，可以选择线性分析，也可以选择曲线估计等其他回归方程。
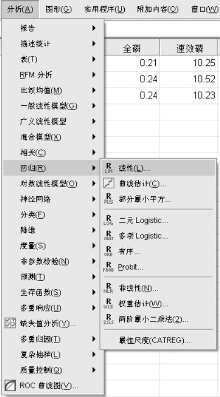
图15-10 线性分析选项示意图
五、均值的比较与检验
T检验是检验差异显著性的十分重要的统计工具，这种差异显著性的检验是样本均值间的比较。因此T检验也可以称为一种均值比较分析。它包括单样本T检验、独立样本T检验、配对样本T检验。
来自正态总体的两个样本进行均值比较常使用T检验的方法。T检验要求两个被比较的样体来自正态总体。
两个样本方差相等与不等时使用的计算t值的公式不同。
1．单样本T检验。
检验单个变量的均值是否与给定的常数之间存在差异。样本均数与总体均数之间的差异显著性检验属于单一样本T检验。
例如，六块样地土壤有机质平均含量为18．22，比较各样地土壤有机质含量平均数与六块样地所有有机质平均数之间是否存在显著性差异。
将左边有机质导入右边检验变量框中，输入检验值18．22，点击确定见图15-11，即可得到比较结果见表15-6。
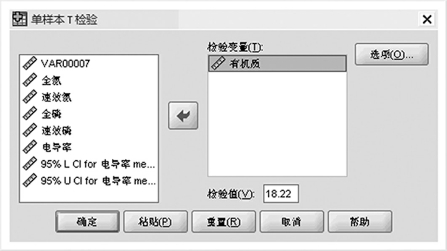
图15-11 单样本T检验分析选项卡
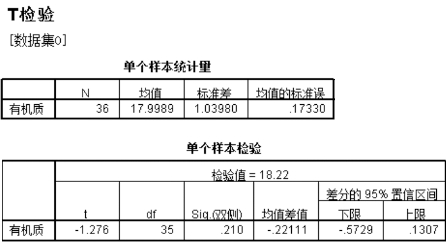
表15-6 T检验输出结果
2．两独立样本T检验。
进行独立样本T检验，要求被比较的两个样本彼此独立，即没有配对关系。要求样本均来自正态总体，而且均值对于检验是有意义的描述统计量。
独立样本T检验和配对样本的T检验均使用T test过程，但是使用的菜单不同对于数据文件结构的要求和所使用的命令语句也有区别。
例如，某土壤样地2017年与2016年速效氮含量分别为
假定2017年和2016年土壤速效氮含量都服从正态分布，且方差相同，问2017年和2016年土壤速效氮含量平均之间是否有显著变化（p＜0．05）？
同样是数据输入完成后，依次点击“分析—比较均值—独立样本T检验”（图15-12）。
图15-12 两独立样本T检验分析路径
将速效氮导入检验变量，分组导入分组变量，点击定义组，在弹出的右边所示对话框中组一和组二后面填数字1和2，然后点击继续—确定见图15-13，输出结果如下图所示15-7。
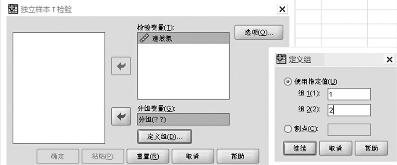
图15-13 两独立样本T检验分析
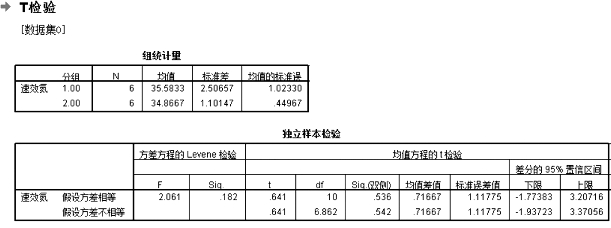
表15-7 两独立样本T检验分析输出结果
有关生态数据分析与建模的文章
- 详细阅读
-
Origin概述：生态数据分析与建模详细阅读
Origin是Windows平台下用于数据分析、项目绘图的软件，是科技工作者进行数据分析与科学绘图的高端软件作品，具有功能强大、使用方便的特点。Origin带给用户的是最直观、最简单的数据分析和绘图环境。Origin像Microsoft Word、Excel等一样，是一个多文档界面。Origin最突出的优点是使用简单，采用直观的、图形化的、面向对象的窗口菜单和工具栏操作。图17-1Origin的工作界面Origin目录下包括8个子目录，还有大量的模板文件和配置文件。......
2023-11-17
-
《生态数据分析与建模》：土壤数据的重要性及分详细阅读
土壤无论对植物来说还是对土壤动物来说都是重要的生态因子。由于在土壤中运动要比大气中和水中困难得多，所以除了少数动物能在土壤中掘穴居住外，大多数土壤动物都只能利用枯枝落叶层中的孔隙和土壤颗粒间的空隙作为自己的生存空间。因此，土壤数据包括野外调查数据，比如枯枝落叶层的厚度、土壤类型、土壤厚度和剖面特征、土壤温度等。室内测定数据包括土壤结构、土壤容重、土壤水分、土壤物理特性及化学特性。......
2023-11-17
-
生态数据分析与建模：回归分析问题与原因详细阅读
在多数生态学文献中，回归分析方面的问题是所有应用统计学中出现频率最高的问题。R2实际上是一个相对的度量，它表示回归平方和占总平方和的百分比。......
2023-11-17
-
目录和命令菜单-《生态数据分析与建模》详细阅读
Origin提供两种菜单：全部菜单和简略菜单，默认值为全部菜单。工具栏中的图形按钮和菜单栏中的某一菜单功能相同，例如下图17-2。图17-2数字编辑区的快捷菜单要编辑的区域内点击右键，会出现对应区域的快捷菜单：1．工具栏。Origin为经常使用的菜单命令定制了按钮工具栏，每个按钮工具栏中的按钮只有当前窗口能使用到它时，它才被激活。......
2023-11-17
-
生态数据分析与建模：数据标准化方法及实例详细阅读
为了消除量纲影响和变量自身变异大小和数值大小的影响，故将数据标准化。经过标准差标准化后，数据都是没有单位的纯数量。尽管如此，它还是当前用得最多的数据标准化方法，也是SPSS中最为常用的标准化方法。即第三步，再对变量进行标准差标准化，即将某变量中的观察值减去该变量的平均数，然后除以该变量的标准差。表13-7长江17个观测点的水质分析表数据转换步骤如下：1．数据的标准化处理。......
2023-11-17
-
生态统计学概述-《生态数据分析与建模》成果详细阅读
生态统计学是运用概率论和数理统计的原理与方法，指导生态学的试验调查设计，分析试验调查资料，进而发现普遍规律的一门学科。生态统计学主要介绍生态学的试验设计，试验数据的收集、整理、分析，并推断、发现和解释生态学现象的本质规律。因此，生态统计学是生态学专业学生培养的重要基础课程之一，越来越受到高等院校的重视。生态统计学研究内容见图1-1。......
2023-11-17
-
生态数据分析与建模的验证与规划详细阅读
在完成建模过程之后，就是验证。对于验证可定义如下：如果模型运行符合建模者的要求，就可称模型已被验证。建模者必须多次重复该过程，直至验证和校准阶段的模型输出能使建模者满意。验证的这一部分在很大程度上是以主观标准为依据的。在验证阶段还应检查模型的长期稳定性。遗憾的是，由于缺乏时间，许多模型还没有经历适当的验证。因此，强烈建议在建模过程中的这一重要阶段，应花费足够的时间去验证并规划必要的资源分配。......
2023-11-17
相关推荐