首页理论教育生态数据分析与建模：直线回归假设测验

生态数据分析与建模：直线回归假设测验

2025-09-30 理论教育版权反馈

【摘要】：所以对于样本的回归方程，必须测定其来自无直线回归关系总体的概率大小。所以对直线回归的假设测验为H0：β＝0对HA：β≠0由（6-3）式可推得回归系数b的标准误Sb为：而遵循ν＝n-2的t分布，故由t值即可知道样本回归系数b来自β＝0总体的概率大小。所以，对直线回归作假设测验，只需选择上述测验方法之一即可。

一、回归关系的假设测验

若X和Y变数总体并不存在直线回归关系，则随机抽取的一个样本也能用上节方法算得一个直线方程＝a＋bx。显然，这样的回归方程是靠不住的。所以对于样本的回归方程，必须测定其来自无直线回归关系总体的概率大小。只有当这种概率小于0．05或0．01时，我们才能冒较小的风险确认其所代表的总体存在着直线回归关系。这就是回归关系的假设测验，可由t测验或F测验给出。

1．t测验由（6-4）式可推知，若总体不存在直线回归关系，则总体回归系数β＝0；若总体存在直线回归关系，则β≠0。所以对直线回归的假设测验为H0：β＝0对HA：β≠0

由（6-3）式可推得回归系数b的标准误Sb为：

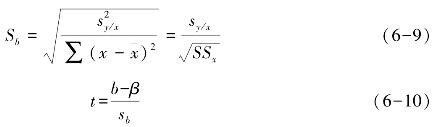
pagenumber_ebook=50,pagenumber_book=38

而遵循ν＝n-2的t分布，故由t值即可知道样本回归系数b来自β＝0总体的概率大小。

［例2］试测验［例1］资料回归关系的显著性。

已算得b＝-1．099 6，SSx＝144．635 65，sy/x＝3．266故有

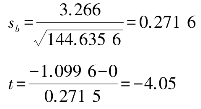
pagenumber_ebook=50,pagenumber_book=38

查附表2，t0．05，7＝2．36，t0．01，7＝3．50。现实得｜t｜＝4．05大于t0．01，7，表明在β＝0的总体中因抽样误差而获得现有样本的概率小于0．01。所以应否定H0：β＝0，接受HA：β≠0，即认为积温和代三化螟盛发期是有真实直线回归关系的，或者说此b＝-1．099 6是极显著的。

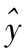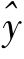2．F测验当仅以 pagenumber_ebook=45,pagenumber_book=33 表示y资料时（不考虑x的影响），y变数具有平方和SSy＝∑2和自由度ν＝n-1。当以 pagenumber_ebook=47,pagenumber_book=35 ＝a＋bx表示y资料时（考虑x的影响），则SSy将分解成两个部分，即：

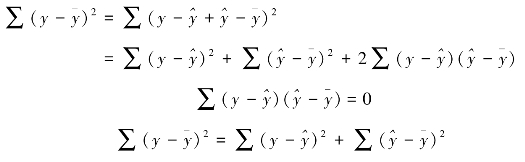
pagenumber_ebook=50,pagenumber_book=38

上式的∑2即离回归平方和Q，它和x的大小无关，具有ν＝n-2，已如前述；∑2则为回归平方和，简记作U，它是由x的不同而引起的，具有ν＝（n-1）-（n-2）＝1。在计算U值时可应用公式：

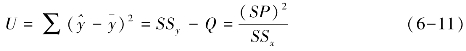
pagenumber_ebook=51,pagenumber_book=39

由于回归和离回归的方差比遵循ν1＝1，ν2＝n-2的F分布，故由

pagenumber_ebook=51,pagenumber_book=39

即可测定回归关系的显著性。

［例3］试用F测验法检测［例1］资料回归关系的显著性。

已算得SSy＝249．555 6，Q＝74．667 0，故U＝249．555 6-74．667 0＝174．888 6，并有方差分析列于表6-3。

表6-3　例1资料回归系数的方差分析

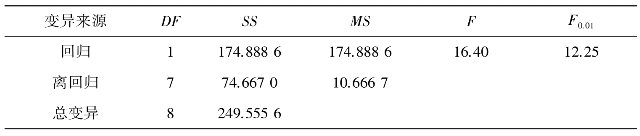
pagenumber_ebook=51,pagenumber_book=39

在表6-3，得到F＝16．40＞F0．01，所以同样表明积温和一代三化螟盛发期是有真实直线回归关系的，即β≠0（准确地说，在β＝0的总体中获得现有回归样本的概率小于0．01）。(https://www.chuimin.cn)

上述t和F测验，在任何回归样本上的结果都完全一致。因为在同一概率值下，ν1＝1、ν2＝n-2的一尾F值正好是ν＝n-2的两尾t值的平方即F＝t2。如本例，F＝16．40，t＝-4．05，（-4．05）2＝16．40。事实上，由（6-12）式可作恒等变换。

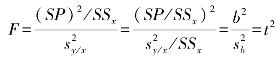
pagenumber_ebook=51,pagenumber_book=39

所以，对直线回归作假设测验，只需选择上述测验方法之一即可。

二、两个回归系数比较时的假设测验

若有两个直线回归样本，分别具有样本回归系数b1、b2和总体回归系数β1、β2，则在测验b1和b2的差异显著性时，有H0：β1-β2＝0对HA：β1-β22≠0。

由抽样分布的理论可以推知（参见抽样分布的标准误公式），两个样本回归系数的差数标准误：

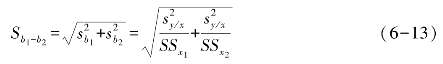
pagenumber_ebook=52,pagenumber_book=40

上式的SSx1和SSx2分别为X变数两个样本的平方和，为两个样本回归估计的合并离回归方差，其值为：

pagenumber_ebook=52,pagenumber_book=40

（6-14）式的Q1和Q2分别为两个样本的离回归平方和，n1和n2为相应的样本容量。

由于（b1-b2）/遵循ν＝（n1-2）＋（n2-2）的t分布，故由

pagenumber_ebook=52,pagenumber_book=40

可测定在β1-β2＝0的总体中获得现有b1-b2≠0的样本的概率。

［例4］测定两玉米品种叶片长宽乘积（x）和实际叶面积（y）的关系，得表6-4结果，试测验两回归系数间是否有显著差异。

表6-4　玉米叶片长宽乘积和叶面积关系的计算结果

pagenumber_ebook=52,pagenumber_book=40

由表6-4可得

pagenumber_ebook=52,pagenumber_book=40

这一结果是完全不显著的，所以应接受H0：β1＝β2，即认为叶片长宽乘积每增大1 cm2，叶面积平均要增大的单位数在品种1和品种2上是一致的，其共同值为：

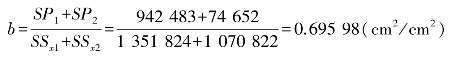
pagenumber_ebook=53,pagenumber_book=41

注意：上式的b是两个回归系数的加权平均数，它不等于（b1＋b2）/2。