静定桁架就属于这种结构体系，单元逻辑图如图4.2所示。因尔，从体系可靠度的角度来看，实际的桥梁应尽量避免做成静定结构，条件允许时，应做成具有适当冗余度的超静定结构。超静定结构就是具有这种特性的结构体系。......
2025-09-30
悬吊结构体系可靠度计算结果与ASVR方法相似
【摘要】：如图4.8所示悬吊结构的构件应力仅受荷载P1和P2的影响。图4.10悬吊结构的失效路径ASVR方法与文献［21］给出的计算结果的误差如表4.4所示。表4.4悬吊结构的体系可靠指标计算结果由表4.4可知，ASVR计算结果与文献［21］提供的数值结果的误差在1%之内，表明ASVR在具有隐式和非线性功能函数的超静定结构的体系可靠度分析中计算精度较高。该悬吊结构的SVR模型被用于拟合结构的响应函数，大大减少了有限元的计算次数。
Frangopol［21］给出了如图4.8所示的具有几何非线性的悬吊结构。该结构整体高度为4m，宽度为15m，由拉索、吊杆和主梁3部分组成，主梁受P1和P2这两个荷载的作用。该结构的确定性参数与随机变量参数分别如表4.2和4.3所示。
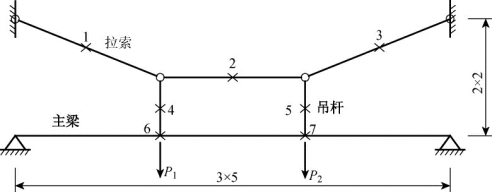
图4.8 某悬吊结构（单位：m）
表4.2 悬吊结构的确定性参数
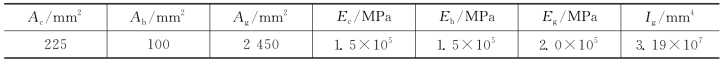
表4.3 悬吊结构的随机变量参数
其中，Ac、Ah、Ag分别表示拉索、吊杆、主梁的截面面积；Ec、Eh、Eg分别表示拉索、吊杆、主梁的弹性模量；Ig表示主梁截面的惯性矩；σc表示拉索的容许应力；σh表示吊杆的容许应力；σg表示主梁的容许应力。如表4.3所示的随机变量均假定服从正态分布，该结构的显式功能函数为：
g2（X）＝A·σ-T （4．35）
g3（X）＝f·Iz／（h／2）·σ-M （4．36）
式中，A和σ为各构件的截面面积和材料的屈服强度；T为构件的轴力；f为塑性铰弯矩与屈服弯矩比值，算例中取为1.167；Iz为截面惯性矩；h＝3表示截面高度；M为主梁的弯矩效应值。
如图4.8所示，假定构件（1～5）的失效模式是强度失效，构件（6～7）的失效模式是弯曲失效。结构体系的两个失效准则定义如下：(https://www.chuimin.cn)
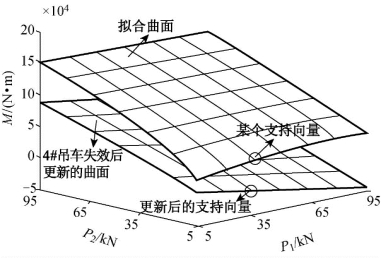
图4.9 4＃吊杆失效前后6＃主梁的拟合响应面
准则一 所有构件中任何一个构件失效则结构体系失效。
准则二 构件（4～7）中任何2个构件同时失效则结构体系失效。
如图4.8所示悬吊结构的构件应力仅受荷载P1和P2的影响。选取均匀设计表U10（102），其中，U表示均匀设计，10表示样本容量为10，2表示变量个数为2个，在每次支持向量更新时采用的样本点数量均为10。为了描述ASVR流程图中的第二个更新步骤，在4＃吊杆失效前后6＃主梁的弯矩拟合图如图4.9所示。两个失效准则的失效构件及对应的可靠指标如图4.10所示。
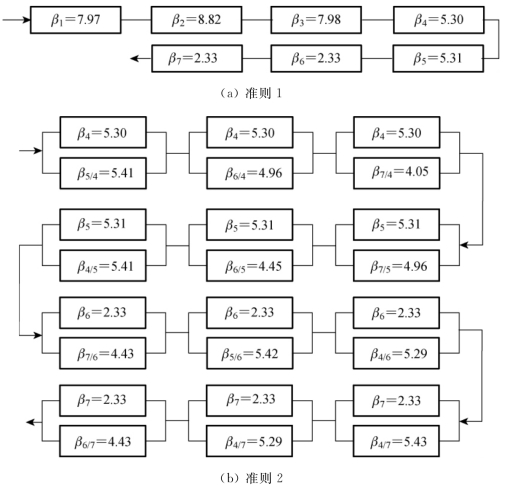
图4.10 悬吊结构的失效路径
ASVR方法与文献［21］给出的计算结果的误差如表4.4所示。
表4.4 悬吊结构的体系可靠指标计算结果
由表4.4可知，ASVR计算结果与文献［21］提供的数值结果的误差在1%之内，表明ASVR在具有隐式和非线性功能函数的超静定结构的体系可靠度分析中计算精度较高。该悬吊结构的SVR模型被用于拟合结构的响应函数，大大减少了有限元的计算次数。与现有的MCS相比，ASVR模型替代了有限元模型，降低了有限元的计算次数；与传统的RSM-β约界法相比，ASVR模型能够拟合高次非线性特征，准确地识别出关键失效构件。因此，ASVR的计算精度优于RSM-β算法，而计算效率优于MCS方法。
相关文章
- 详细阅读
-
桥梁结构简化措施及可靠度分析方法详细阅读
大跨度桥梁多为超静定结构，力学特征复杂，构件失效概率较低，精确计算不可行。若主梁的任一构件失效时都会导致结构整体失效，则该结构就可模型化为串联结构体系。超静定结构的失效路径繁多，若考虑所有的失效模式，计算量变得复杂。在一个结构的所有失效模式中，只有一小部分失效模式对结构体系失效概率的结果影响较大，而大部分失效模式对其影响较小，可以忽略不计。设某桥梁结构的基本随机变量为X1、X2、…......
2025-09-30
-
混凝土结构设计计算的结构可靠性与可靠度详细阅读
结构设计的目的，就是要使所设计的结构在规定的时间内能够在具有足够可靠性的前提下，完成全部预定功能的要求。由此可见，结构可靠度是结构可完成“预定功能”的概率度量。这里所说的“规定时间”是指对结构进行可靠度分析时，结合结构使用期，考虑各种基本变量与时间的关系所取用的基准时间参数；“规定的条件”是指结构正常设计、正常施工和正常使用的条件，即不考虑人为过失的影响；“预定功能”是指上面提到的4项基本功能。......
2025-09-30
-
桥梁可靠度分析：简化Brotonne斜拉桥结详细阅读
法国Brotonne斜拉桥主跨320m，其简化结构如图3.12所示。为验证联合智能算法在斜拉桥的简化结构体系可靠性分析中的可行性，以Brotonne斜拉桥的简化结构为例，计算在承载能力极限状态下斜拉索强度失效和主梁弯曲失效的结构体系可靠度。图3.12Brotonne斜拉桥的构件编号图图3.12中的“3×37”表示拉索间距为37m，共3段间距。图3.13Brotonne斜拉桥的失效树和计算图最后由图3.13所示的失效树与串并联关系计算图可计算出体系可靠指标上下限分别为3.1571和3.1103。......
2025-09-30
-
桥梁抽样方法分析-桥梁可靠度分析方法与应用详细阅读
一般的MC法用于高度非线性的极限状态曲面或者随机变量维数较高的情况，使用在笛卡儿坐标下的抽样模拟法效率较低，计算耗时较多。因此，Ditlevsen、Olesen、Mohr提出了在标准正态空间中极坐标下进行抽样的方向抽样MC法。③重复步骤①和②直到N次，利用式估计失效概率。对于极限状态曲面接近球面的情况，方向抽样MC法比笛卡尔坐标空间的MC法占较大的优势，若计算接近平面的极限状态曲面时，则无优势。......
2025-09-30
-
桥梁可靠度分析方法及应用详细阅读
Rocco等［4］提出了联合SVM和MCS求解结构可靠度的方法。SVM在结构体系可靠度分析中的应用较少。为了发展工程结构体系可靠度理论与方法在桥梁安全评估中的应用，本章将建立桥梁结构体系可靠度分析的简化模型，总结现有结构体系可靠度分析方法，提出基于支持向量机的桥梁结构可靠度分析方法，最后采用两个算例分析表明支持向量机在桥梁结构体系可靠度评估中的应用。......
2025-09-30
-
连续刚构桥的可靠度分析方法与应用详细阅读
图3.14主梁截面图为减少计算量，只取主跨的单幅桥进行计算。表3.4系数随机变量分布成桥后的随机变量需要考虑到活载Q2对结构的影响，拟合出的失效模式功能函数为：本章采用响应面法对某高墩大跨连续刚构进行了体系可靠度计算分析。该算例在分析的响应面方法、结构有限元分析和结构可靠度理论的基础上，实现了连续刚构桥的体系可靠度分析。......
2025-09-30
-
桥梁可靠度分析方法与应用-验算点法详细阅读
针对中心点法计算精度较低的问题，Hasofer和Lind等提出了验算点法［2］。图2.1当量正态化示意图图2.2n维空间的极限状态曲面图假设受n个非正态分布随机变量影响的结构极限状态方程为：Z＝g（X1，X2，…由公式（2.3）、和联立可求解可靠指标β和验算点。值得注意的是，在由Newton迭代法求出β值后，按式计算原坐标系中的验算点时，应区分正态分布和非态分布参数的μXi值。......
2025-09-30
相关推荐