它的透视为其本身，因两个平面交线为一直线，故平面的迹线必为一条直线。平面的灭线也是平面上各直线的灭点的集合。......
2025-09-29
视点与建筑物的位置关系及其画面表现
【摘要】：图6-36斜透视图6-36斜透视图6-37画面前后位置不同时的透视6.5.2.2画面同建筑物的前后关系画面的方向虽已确定，但尚可前后移动。
6.5.2.1 画面同建筑物的方向关系
1.正面透视
画面平行于建筑物的正面或一个较为主要的竖直面时的透视，称为正面透视或平行透视。对于一个长方体来讲，此时的水平面和另一个方向的竖直面，垂直于画面。在这种情况下，画面有平行于建筑物的竖直线和一组水平线，这两组直线没有灭点；另一组水平线，因垂直于画面而有一个灭点s′，故这种透视也称为一点透视。
对于左右对称的建筑物，正面透视尚可分为两种。
（1）中心正面透视，即主视线Ss′的左右位置，恰对准正面的竖直对称线，如图6-34 （a）所示。
（2）偏心正面透视，视点偏向一侧，如图6-34 （b）所示。
正面透视适用于有对称建筑的广场、会场，也适用于街道、庭院、进口处和室内等，尤其适用于U形建筑物，以及要求表示正面的真正形状，正面有复杂的曲线等图形时。中心正面透视，显得庄严伟大；偏心正面透视，较为生动，并可见到一个侧面多些。
2.成角透视
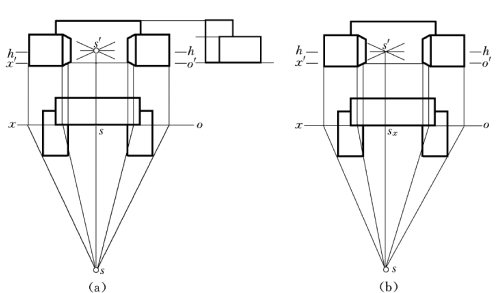
图6-34 正面透视
（a）中心正面透视；（b）偏心正面透视
画面与建筑物的水平面垂直，但与两个方向竖直面均倾斜而具有夹角时的透视，称为成透视。对于长方体来讲，此时的竖直线因平行于画面而无灭点，只有两组水平线与画面相交，有两个灭点，故这种透视也称为两点透视。成角透视的应用最广，较正面透视生动活泼。且我们日常视物时，往往不是面对建筑物的正面，而是从倾斜方向观看的。故成角透视符合客观视物时情况，成角透视尤其广泛地应用于单体建筑物。
成角透视中，正面对画面的夹角β最好在30°左右，如图6-35所示。若夹角大于45°，侧面变宽，失去了原有建筑物的长宽比，如图6-35 （a）所示；若夹角β较小，侧面显得较窄，如图6-35 （c）所示。
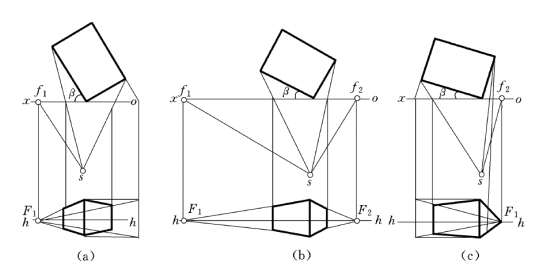
图6-35 成角透视的偏转角
（a）β较大；（b）适中；（c）偏小
3.斜透视
画面与建筑物如长方体的各面均倾斜时的透视，称为斜透视。对长方体来讲，这时画面对长方体的三种方向直线均不平行，故有三个灭点，即竖直线亦有灭点F3，故这种透视，也称为三点透视。斜透视常用于表示高耸建筑物或建筑物群体，如图6-36所示。
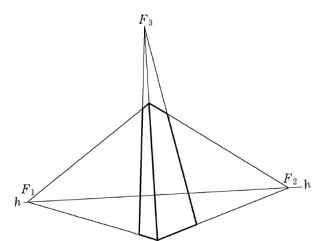
图6-36 斜透视
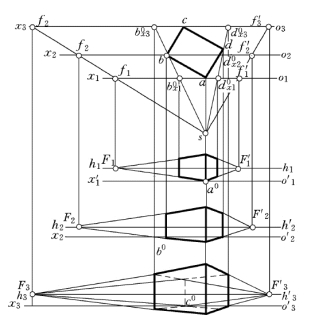
图6-37 画面前后位置不同时的透视
6.5.2.2 画面同建筑物的前后关系(https://www.chuimin.cn)
画面的方向虽已确定，但尚可前后移动。即视点位置决定后，若画面离视点近时，所得透视图的图形小；若画面离视点远时，所得透视图的图形则大。但透视的形状相似，如图6-37所示。
（1）画面置于建筑物之前，即画面置于建筑物与视点之间，如o1x1位置等。此时，建筑物上诸画面平行线的透视，较实长短，故也称为缩小透视。
（2）画面置于建筑物之后，如o3x3位置。此时，建筑物上画面平行线的透视，较实长为长，故也称为放大透视。但在这种情况下，若视线的H 面投影较长；稍有不准，则与ox轴的交点的误差也大，影响透视的准确性。
（3）画面穿过建筑物时，如o2x2位置，没有专门名称。
习惯上使得画面通过建筑物墙角线，非但其透视即为本身，且使某些水平线的迹点在该线上，可使作图方便。
6.5.2.3 视点离开画面的远近关系
若画面与建筑物的相对位置已经决定，视点离开建筑物的视距不同时，将产生形状和大小略有不同的透视。视距大时透视图形大，水平线的透视方向平缓；视距愈小，透视图形也愈小，透视方向愈陡。如图6-38中，离ox距离大时的视点s1的透视图形，要比视距小时的s2的透视图形大。
6.5.2.4 视点与建筑物相对高度的关系
1.一般的透视
一般的透视，即视点不低于高于建筑物时的透视，如图6-39中视平线为h2—h2的位置。此时的透视无特殊名称。
图6-38 视距不同时的透视
当人立于水平的地面上，视高为1.4～1.7m时，可取1.5m。
绘制室内透视时，如房间高度大，取视高1.0～1.3m，好像坐着观看一样。这样房间好像大些和开朗些，有宽敞感。但若要表示家具排列，则视高亦可高些。特别对于礼堂、剧场、运动场等，为了显示座位排列，则视点可更高些。
绘制室内透视，也可以把靠近观者的墙壁拆去后观看，即采用剖视的方法。
2.鸟瞰图
视点高于建筑顶面时的透视，称为鸟瞰图，如图6-39中视平线h3—h3位置时，这时好像在空中、山上或其他更高的建筑上观看时情况。
鸟瞰图除能表示建筑物顶部形状外，更广泛地应用于范围较大的建筑群，甚至希望能越过较近的建筑物来看到后方的建筑物、庭院内部等，此时画面可以是竖直的，也可以是倾斜的。
3.仰望透视
视点低于建筑物时的透视，称为仰望透视。如图6-39中视平线为h1—h1时。也好像在山下观看山上建筑物，或者观看檐口、平顶等情况。此时，画面是竖直的，也可以是倾斜的。
图6-39 视点高低不同时的透视
相关文章
- 详细阅读
-
刚体绕轴转动及其物理量的关系详细阅读
刚体的这种运动称为刚体绕定轴转动，简称转动。φ 为代数量，并规定刚体按逆时针方向转动时，转角φ 取正值；反之取负值。显然，当转角φ 已知时，刚体的位置也随之确定。即上式表明，刚体绕定轴转动的角速度等于转角对时间的一阶导数。N 与ω 的关系是角加速度是描述刚体转动角速度变化快慢的物理量。图10-10刚体绕定轴转动建立Ox 坐标，以轴Ox 与圆周交点MO 作为运动的起始点，并以此点作为弧坐标S 的原点。......
2025-09-29
-
一般位置的直线投影及其特性介绍详细阅读
对一般位置直线来说，其实长和倾角不能直接在投影图中定出，可根据投影用作图的方法来求得，这种方法是直角三角形法。一般位置直线在三面投影体系中的直观图如图2-34所示。图中ab、a′b′是一般位置线AB 的两面投影，为已知条件。......
2025-09-29
-
时尚与个体的相互关系详细阅读
西美尔认为时尚外在于个体，时尚向个体展现的易变性是个体自我稳定感的对照，在对照中，个体的自我感意识到自身的相对持续性。随后西美尔对于时尚与个体、时尚与阶级之间关系的论述都是以上面两点为基础和前提的。西美尔认为，作为一种大众行为，时尚可以帮助个体克服羞耻感。在接下来关于时尚与个体关系的论述中，西美尔强调了个体的心理因素对于个人时尚和社会时尚的影响。......
2025-09-29
-
自动扶梯的安装位置选择在建筑物内的重要因素详细阅读
自动扶梯在建筑物中的安装位置称为自动扶梯的井道。在需要时，自动扶梯也可以在提升高度达10m时才设中间支承，但此时桁架需要做得相当粗壮，上下端部的支承力F1、F2也需要很高。......
2025-09-29
-
淀粉分支酶及其与稻米食味品质的关系详细阅读
淀粉分支酶又称Q酶，在支链淀粉结构形成中有重要的作用。根据淀粉分支酶作用的底物和形成的分支链长，可将同工型分为SBEI和SBEII两个家族。A型的突变体中，直链淀粉含量高，支链淀粉分支减少且分支链增长。Chrastil等认为，淀粉分支酶变化动态与支链淀粉聚合度、链的长度、链数有关，而这些结构都与稻米食味品质紧密相关。......
2025-09-29
-
关于变量相关关系的探讨与分析详细阅读
以两个变量为例进行讨论。这种关系x与y的关系点杂乱无章，如图X3.15所示。相关关系，指两个变量x与y之间的关系介于完全相关和零相关之，这种关系x与y的关系点呈带状分布趋势，如图X3.16所示。图X3.15零相关示意图图X3.16相关关系示意图直线相关；曲线相关例如，流域年径流深与年降水量之间的关系，就是相关关系。......
2025-09-29
- 详细阅读
相关推荐