【主要内容】1.二维连续型随机变量及其概率密度的定义设(X,Y)是二维随机变量,如果存在非负可积函数f(x,y)(-∞
2025-09-30
随机变量数学期望解析
【主要内容】
1.随机变量数学期望的定义
(1)离散型情形设X是离散型随机变量,它的分布律为P(X=xi)=pi(i=1,2,…).如果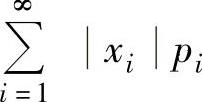
收敛,则称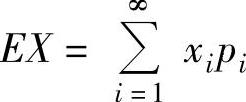 为X的数学期望.
为X的数学期望.
(2)连续型情形设X是连续型随机变量,它的概率密度为f(x)(-∞<x<+∞).如果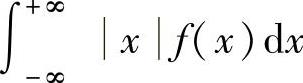
收敛,则称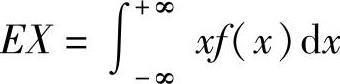 为X的数学期望.
为X的数学期望.
2.随机变量函数的数学期望
(1)离散型情形
设X是离散型随机变量,它的分布律为P(X=xi)=pi(i=1,2,…),又设g(x)是连
续函数,则X的函数g(X)的数学期望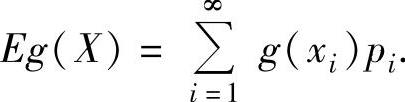
设(X,Y)是二维离散型随机变量,它的分布律为P(X=xi,Y=yi)=pij(i=1,2,…;j=1,2,…),又设h(x,y)是连续函数,则X,Y的函数h(X,Y)的数学期望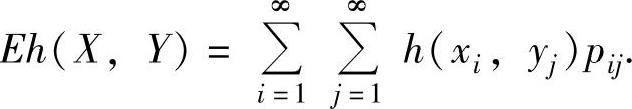
(2)连续型情形
设X是连续型随机变量,它的概率密度为f(x)(-∞<x<+∞),又设g(x)是连续函数,则X的函数g(X)的数学期望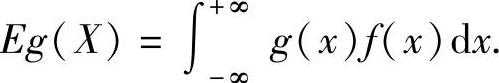
设(X,Y)是二维连续型随机变量,它的概率密度为f(x,y)(-∞<x<+∞,-∞<y<+∞),又设h(x,y)是连续函数,则X,Y的函数h(X,Y)的数学期望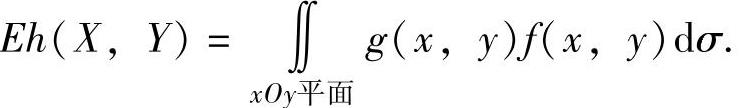
3.数学期望的性质
设X,Y是随机变量,c,c1,c2是常数,则
(1)Ec=c;
(2)E(c1X+c2Y)=c1EX+c2EY;
(3)当X与Y相互独立时,E(XY)=EX·EY.
4.常用随机变量的数学期望
设X服从0-1分布,则EX=p;
设X~B(n,p),则EX=np;
设X~π(λ),则EX=λ;
设X~U(a,b),则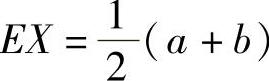 ;
;
设X~E(λ),则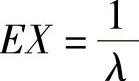 ;
;
设X~N(μ,σ2),则EX=μ.
【典型例题】
例7.16.1 将3只球随机地放入编号为1,2,3,4的四个盒中,以X表示有球盒的最大号码,求EX.
精解 先计算X的分布律.
X全部可能取的值为1,2,3,4,对应的概率为
P(X=1)=P{3只球全部放入1号盒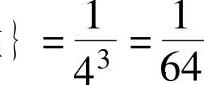 ,
,
P(X=2)=P{3只球中至少有1只放入2号盒,而其余的全放入1号盒}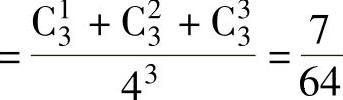 ,
,
P(X=3)=P{3只球中至少有1只放入3号盒,而其余的全放入1号盒或2号盒}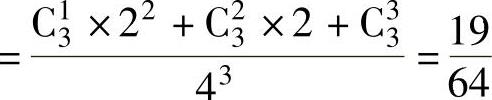 ,
,
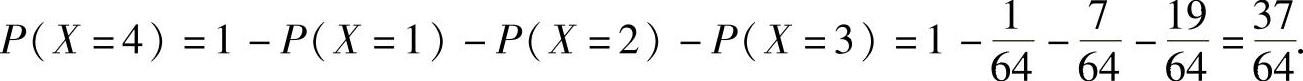
所以由数学期望的定义得
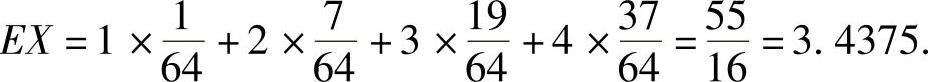
例7.16.2 某车站每天8:00~9:00,9:00~10:00都恰有一辆客车到站,但到站时刻是随机的,且两个时间区间里到站时刻相互独立,具体规律如下:
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
今有一乘客于8:20到车站,求他候车时间X(单位:min)的数学期望.
精解 先写出X的分布律:
X可能取的值为10,30,50,70,90,为了计算对应的概率,记
A1={第一班车8:10到站}, A2={第一班车8:30到站},
A3={第一班车8:50到站}, B1={第二班车9:10到站},
B2={第二班车9:30到站}, B3={第二班车9:50到站},则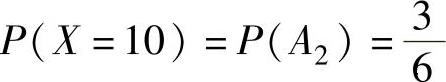 ,
,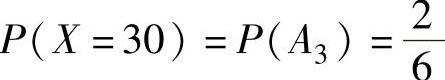 ,
,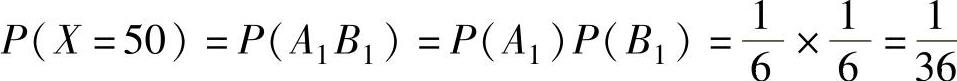 ,
,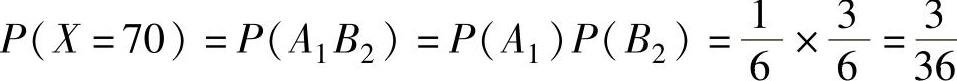 ,
,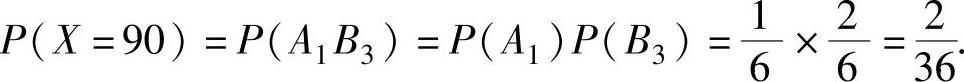 于是,
于是,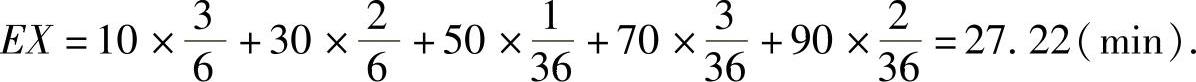
例7.16.3 设连续型随机变量的分布函数为
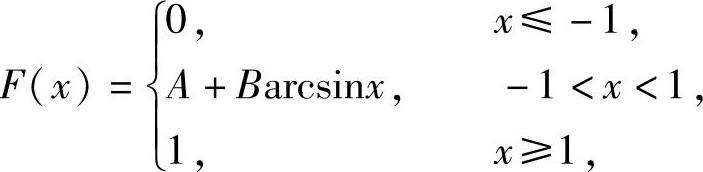
求EX.
精解 先确定常数A,B.
由于F(x)是连续型随机变量的分布函数,所以它是连续函数,特别在点x=-1,1处连续,于是有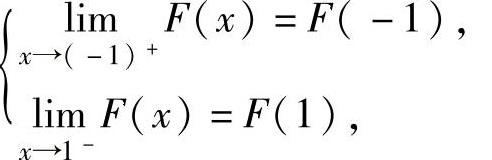 即
即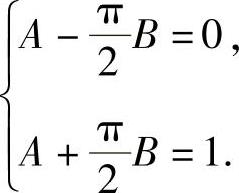
解此方程组得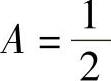 ,
, 因此
因此

由此得到X的概率密度
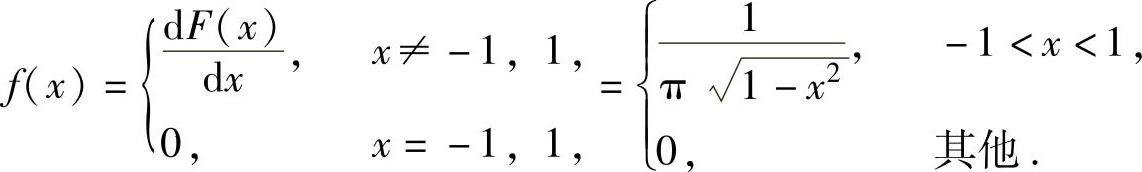
于是,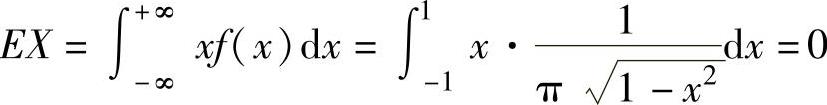 (对称区间上奇函数的积分为零).
(对称区间上奇函数的积分为零).
例7.16.4 设随机变量X与Y分别服从参数均为1的指数分布与泊松分布,求概率P(X2+Y2≤E(X+Y)).
精解 由于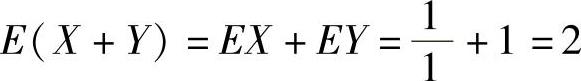 ,所以
,所以
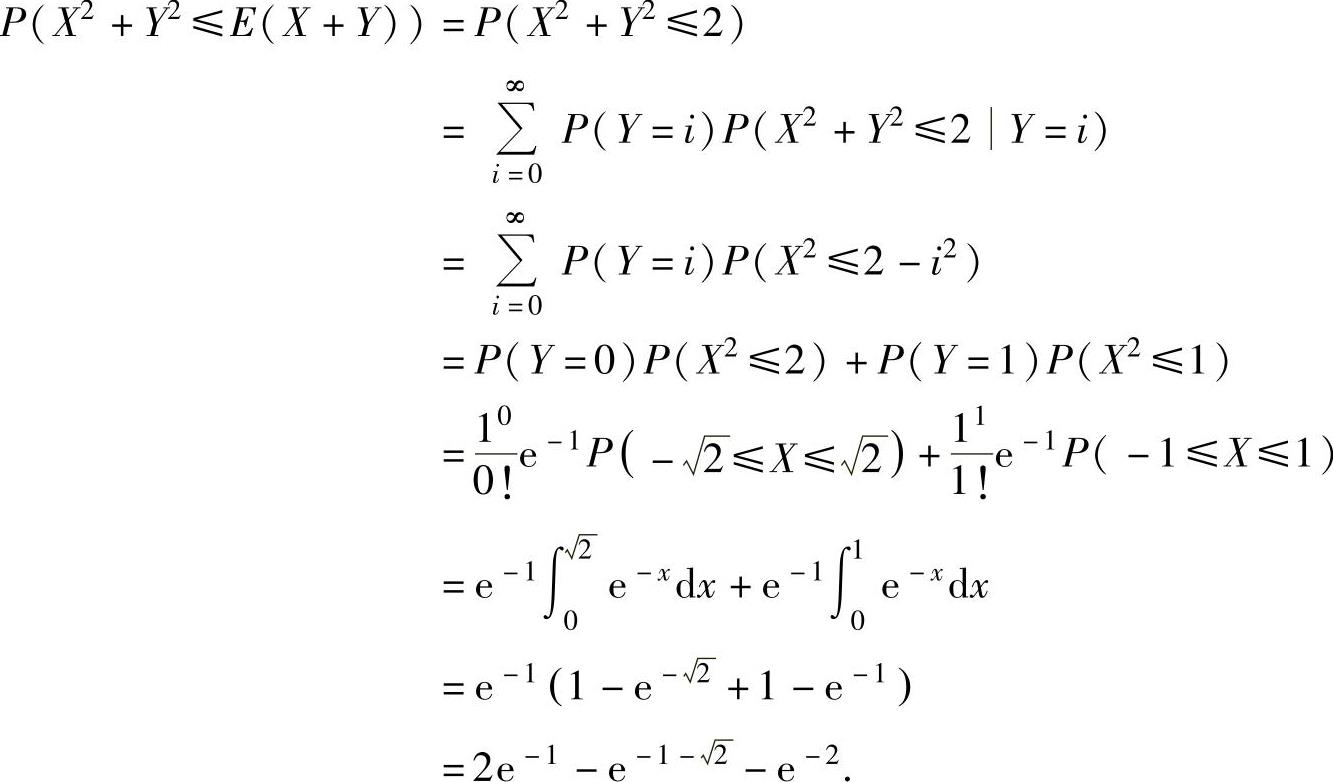
例7.16.5 设随机变量X与Y相互独立,且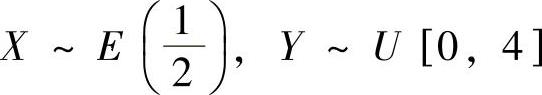 ,求
,求
E(min{X,Y})和E(X+XY+2).
精解 由题设知X与Y的概率密度分别为
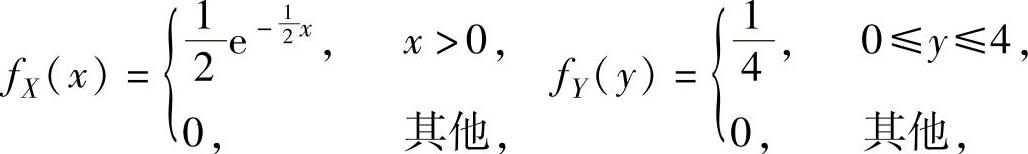
所以,由X与Y相互独立知二维随机变量(X,Y)的概率密度为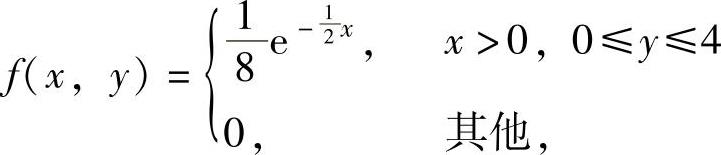 ,
,
即它在D={(x,y)x>0,0≤y≤4}(如图7.16.5阴影部分所示)上取值为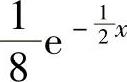 ,在xOy
,在xOy
平面的其他部分取值为零.
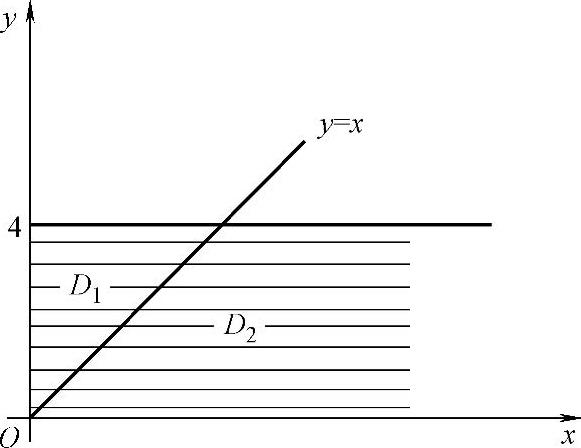
图 7.16.5
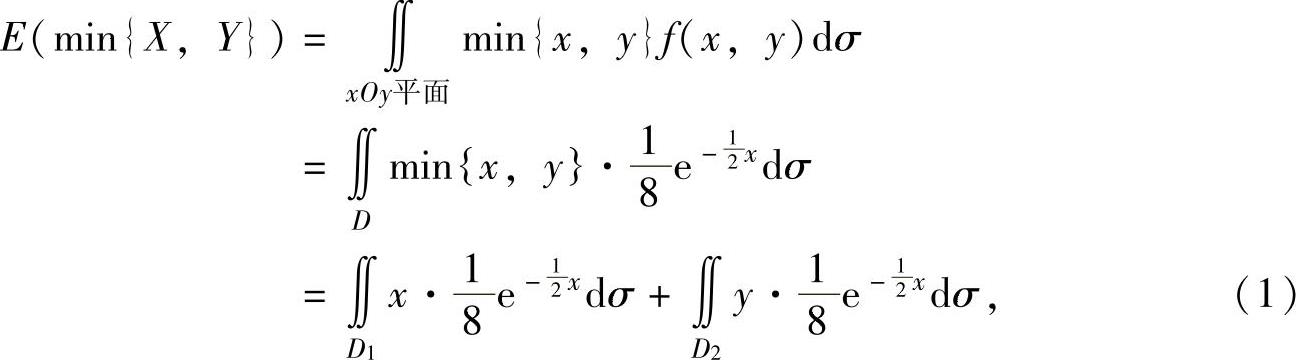
其中,D1与D2是D被直线y=x划分成的两部分,如图7.16.5所示,并且
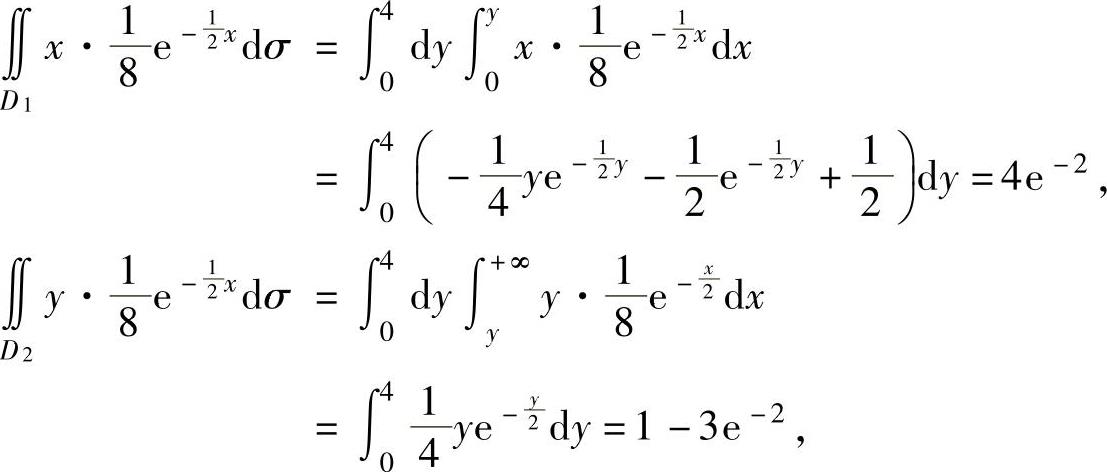
将它们代入式(1)得
E(min{X,Y})=4e-2+(1-3e-2)=1+e-2.下面计算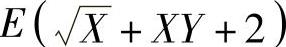

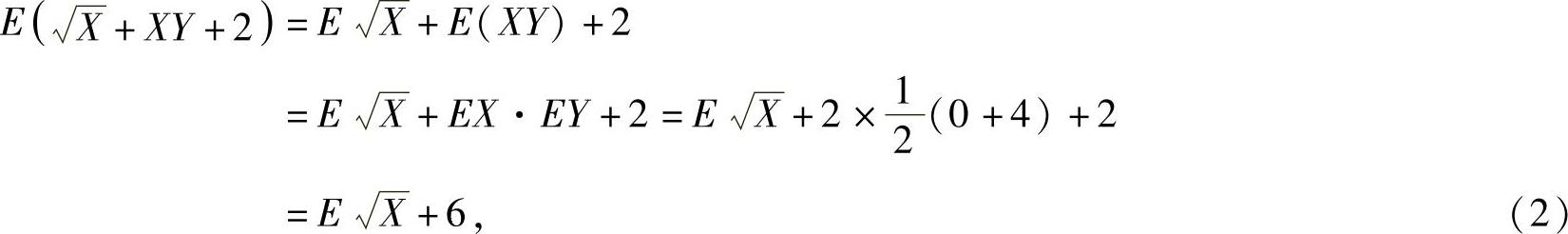
其中,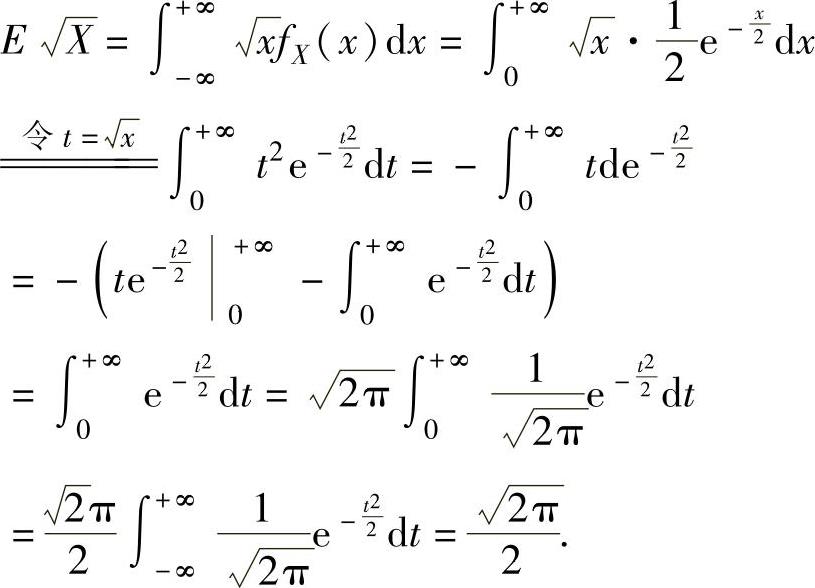
将它代入式(2)得
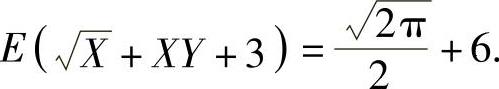
相关文章
- 详细阅读
-
数学教育价值—解析《数学教学论》详细阅读

数学文化的内涵的揭示,决定数学文化的教育价值的转变,影响教育工作者的教育观。所谓教育价值,是指教育对社会或个人等主体的存在或发展具有的意义或价值,数学文化的教育价值表现在科学方面的教育价值和人文方面的教育价值。从我国教育现实情况来看,视数学的教育价值过于工具性,体现在数学在各种考试文化中的核心和关键学科地位。......
2025-09-29
-
离散型随机变量及其分布律解析详细阅读

)为X的分布律,其中pi有以下性质:每个pi>0;Σipi=1.3.常用(一维)离散型随机变量及其分布律服从0-1分布的随机变量设随机变量X的分布律为,则称X是服从以p为参数的0-1分布的随机变量,简称X服从以p为参数的0-1分布,服从二项分布的随机变量设随机变量X的分布律为P(X=k)=Cknpk(1-p)n-k(k=0,1,2,…......
2025-09-30
-
2015考研数学基础篇:二维离散型随机变量及详细阅读

),且取这些值对应的概率为pij(i=1,2,…),p·j=Σipij(j=1,2,…).4.二维离散型随机变量的条件分布律设(X,Y)是二维离散型随机变量,它的分布律及边缘分布律分别为P=pij(i=1,2,…......
2025-09-30
-
坐标变换的数学基础及应用解析详细阅读

上面方程式中的Mu和Mi与所需变换的坐标系相关,因此,该变换矩阵并不是唯一的。如果将式和式代入式可得IU==I′MiMuU′ 从上式可看出,当满足功率不变约束时,必须有下式成立:MiMu=1或者Mi=Mu-1 2.电压和电流具有同一变换系数矩阵的变换采用功率不变约束的变换,虽然能使变换成为唯一,但是其电压变换系数矩阵和电流变换系数矩阵可能并不相同。......
2025-09-29
-
从数学教育到教育数学,解析函数极限新方法详细阅读

既然讲数列极限可以不用“ε-语言”,那么讲函数极限也可以不用“ε-语言”,只不过用“无界不减函数”代替“无界不减数列”罢了。定义7.4.2设f是在[c,+∞)上有定义的函数。用“ε-语言”讲函数极限,常常要一条一条分别给出各种过程中的极限定义。这一套定义,将使学生在学习微积分时免受“ε-语言”之累,在定理证明和做题时用代数运算代替逻辑推理。[例7.4.1]求证:=+∞。......
2025-09-30
-
2015考研数学基础篇全面复习及解析详细阅读

1.单项选择题(1)A (2)C (3)D (4)B (5)C(6)C (7)D (8)C (9)D (10)D(11)A (12)A (13)C (14)B2.解答题(1)φ′(x)=f1′·2x+f2′(f1′·2x+f2′),φ′(1)=2×2+3(2×2+3)=25.(2)对所给方程两边求全微分dz-dx-dy+yez-xdx+xez-xdy+xyez-x(dz-dx)=0,即(1+xye......
2025-09-30
-
国际数学课程改革:新理念解析详细阅读

大众化、活动化、生活化、个性化是世界各国新一轮数学课程改革的普遍取向,集中体现了国际上数学课程改革最为基本的一些共同理念。总之,上述诸改革理念是互相联系着的,科学地将这些思想应用于数学教育的实际活动,包括教材编写与实际的教学工作,将会有益于新一轮的国际数学课程改革。......
2025-09-29


相关推荐