首页理论教育2015考研数：一维随机变量的分布函数简介

2015考研数：一维随机变量的分布函数简介

2023-10-27 理论教育版权反馈

【摘要】：）时，X的分布函数F当X的分布函数为F，其中x1，x2，…

【主要内容】

1.（一维）随机变量分布函数的定义与性质

设X是随机变量，则称F（x）=P（X≤x）（-∞<x<+∞）为X的分布函数.

分布函数的性质：设F（x）是X的分布函数，则

（1）0≤F（x）≤1；

（2）

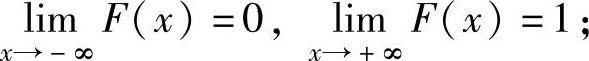
（3）F（x）是单调不减函数；

（4）F（x）是右连续函数.特别地，当X是连续型随机变量时，F（x）是连续函数.

注（ⅰ）以上（1）～（4）也是F（x）为某个随机变量的分布函数的充分条件.

（ⅱ）对于常数c，P（X=c）=F（c）-F（c-）.

2.（一维）随机变量的分布函数与分布律或概率密度之间的关系

（1）离散型情形

设X是离散型随机变量，当已知X的分布律为P（X=x_i）=p_i（i=1，2，…）时，X的分布函数F当X的分布函数为F（x），其中x₁，x₂，…，x_n，…是它的间断点时，X的分布律为P（X=x_i）=F（x_i）-F（x_i-）.

（2）连续型情形

设X是连续型随机变量，其分布函数F（x）与概率密度f（x）（-∞<x<+∞）之间有以下关系

【典型例题】

例7.6.1 （单项选择题）设F₁（x），F₂（x）都是分布函数，则（）.

A.F₁（x）+F₂（x）是分布函数 B.aF₁（x）（常数a≠1）是分布函数

C.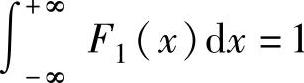D.max{F₁（x），F₂（x）}是分布函数

精解利用分布函数的性质排除其中三个选项即可.对于选项A，B，由于

所以F₁（x）+F₂（x），aF₁（x）都不是分布函数，即选项A，B都不能选.

此外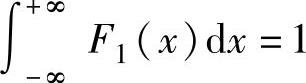显然是错误的，所以选项C也不能选.

因此本题选D

例7.6.2 （单项选择题）设F₁（x），F₂（x）为两个分布函数，其相应的概率密度f₁（x），f₂（x）是连续函数，则必为概率密度的是（）.

A.f₁（x）f₂（x） B.2f₁（x）F₂（x）

C.f₁（x）F₂（x） D.f₁（x）F₂（x）+f₂（x）F₁（x）

精解由F₁（x），F₂（x）是分布函数知F₁（x）F₂（x）也是分布函数（这是因为0≤F₁（x）F₂（x）≤1，lim_x→-∞F₁（x）F₂（x）=0，lim_x→-∞F₁（x）F₂（x）=1，F₁（x）F₂（x）是单调不减

而且右连续的函数），而且由f₁（x），f₂（x）连续知F₁（x）F₂（x）可导，其导数为概率密度，于是

f₁（x）F₂（x）+F₁（x）f₂（x）=[F₁（x）F₂（x）]′是概率密度.

因此本题选D.

例7.6.3 设口袋里有5个白球，3个黑球，任取出1个球，如果是黑球不放回而另外放入一个白球，这样继续下去，直到取出白球为止，记X为直到取出白球时的取球的次数，求X的分布函数.(www.chuimin.cn)

精解先算出X的分布律，然后求出分布函数F（x）.

X可能取的值为1，2，3，4，并且，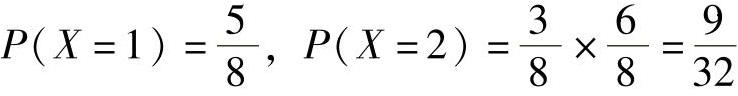

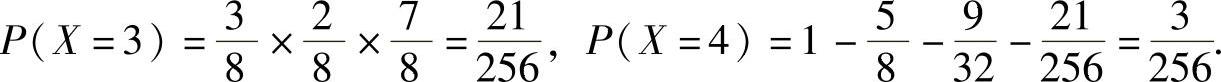
所以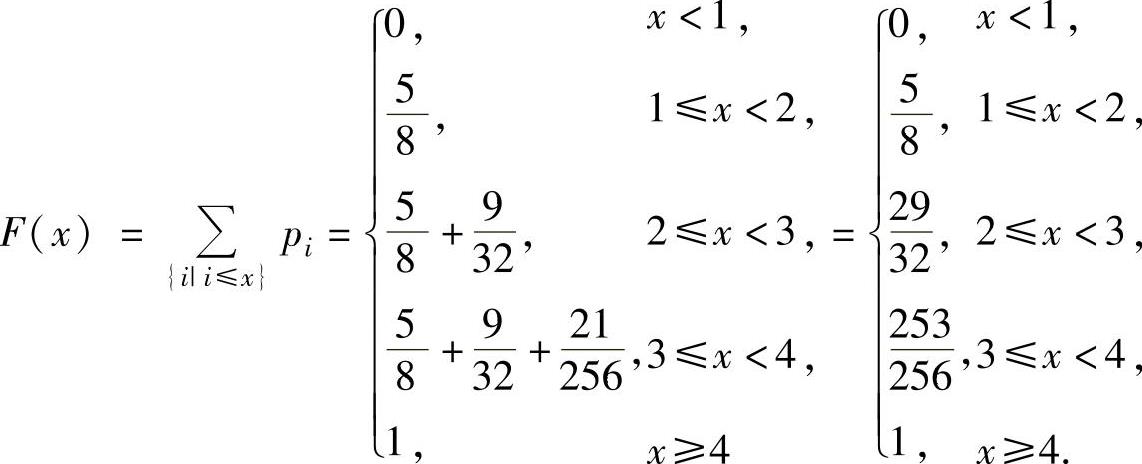

例7.6.4 设随机变量X的分布函数为

求X的分布律及概率P（-1.1<x<3）.

精解 F（x）的间断点x=-1，1，3即为X可能取的值，所以X的分布律为

即

因此，P（-1.1<X<3）=P（X=-1）+P（X=1）=0.4+0.4=0.8.

例7.6.5 设随机变量X的概率密度为

求X的分布函数F（x）.

精解由于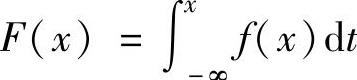，其中f（x）是分段函数，因此对F（x）也与f（x）同样地分

四段计算.

当x≤0时，，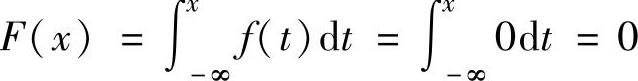

当0<x≤1时，，

当，，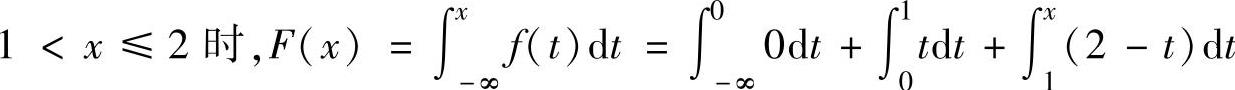

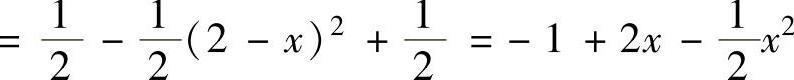当x>2时，，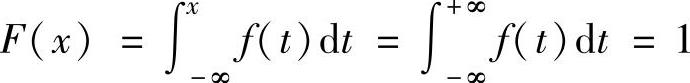

所以，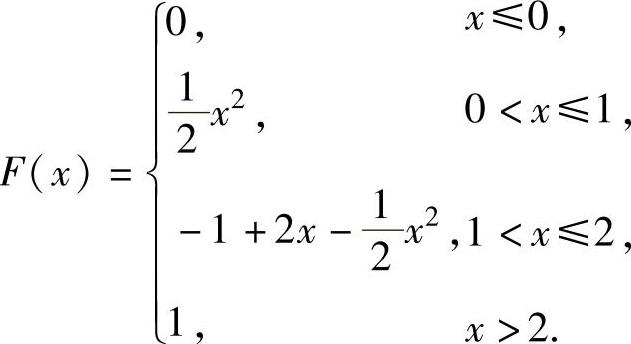

例7.6.6 设随机变量X的分布函数为

求：（1）使F（x）连续的常数A_i（i=1，2，3，4）；

（2）X的概率密度f（x）；

（3）二次方程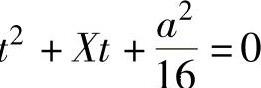的两根都为正根的概率.

精解（1）由于F（x）是分布函数，所以{，即A₁=0，A₄=1.，

此外，为使F（x）连续，特别应使F（x）在点x=-a，a处连续，应有，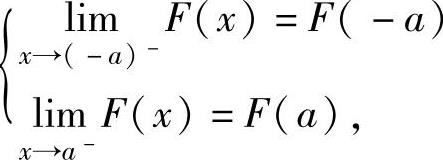

即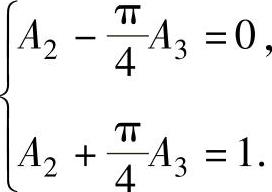（这里利用了A₁=0，A₄=1）.

解此方程组得，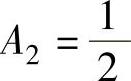

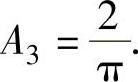
（2）由（1）知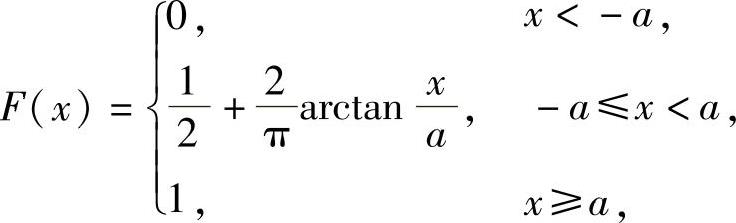所以，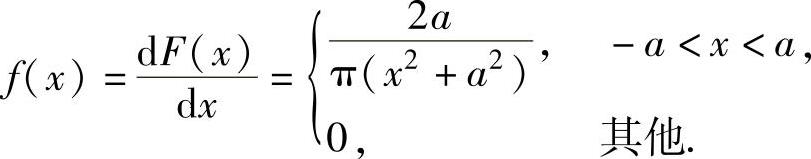

（注意，求导时，x=-a，a处的导数不必具体计算，可直接取为零.）

（3）方程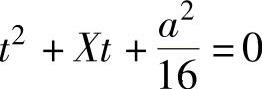的两根都为正根的充分必要条件是

所以其概率为