首页理论教育离散型随机变量及其分布律解析

离散型随机变量及其分布律解析

2025-09-30 理论教育版权反馈

【摘要】：）为X的分布律，其中pi有以下性质：每个pi>0；Σipi=1.3.常用（一维）离散型随机变量及其分布律服从0-1分布的随机变量设随机变量X的分布律为，则称X是服从以p为参数的0-1分布的随机变量，简称X服从以p为参数的0-1分布，服从二项分布的随机变量设随机变量X的分布律为P（X=k）=Cknpk（1-p）n-k（k=0，1，2，…

【主要内容】

1.（一维）随机变量的定义

设随机试验E的样本空间为Ω，则定义在Ω上的实单值函数称为E的一个（一维）随机变量，用X，Y，X_i等表示.

由此可知，随机变量的取值随E的结果而定，在试验之前不能预知它取什么值，且它的取值有一定的概率.

2.（一维）离散型随机变量及其分布律

设随机变量X的全部可能取到的值是有限多个或可列无限多个，则称X为（一维）离散型随机变量.

设X是离散型随机变量，它全部可能取到的值为x₁，x₂，…，x_k（或x₁，x₂，…，x_n，…），对应的概率为p₁，p₂，…，p_k（或p₁，p₂，…，p_n，…），则称

或

（简写为P（X=x_i）=p_i，i=1，2，…，k）（简写为P（X=x_i）=p_i，i=1，2，…，n，…）为X的分布律（或概率分布），其中p_i有以下性质：

（1）每个p_i>0；

（2）Σ_ip_i=1.

3.常用（一维）离散型随机变量及其分布律

（1）服从0-1分布的随机变量设随机变量X的分布律为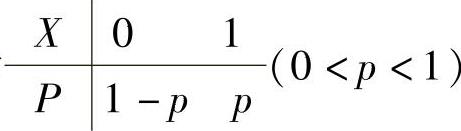，则称X是服从以p为参数的0-1分布的随机变量，简称X服从以p为参数的0-1分布，

（2）服从二项分布的随机变量

设随机变量X的分布律为P（X=k）=C^k_np^k（1-p）n-k（k=0，1，2，…，n），则称X是服从参数为n，p（n为正整数，0<p<1）的二项分布的随机变量，简称X服从参数为n，p的二项分布，记X～B（n，p）.

注设随机试验E只有两个可能的结果A与A，且P（A）=p（0<p<1）.现将E独立重复进行n次（称这一串试验为n重伯努利试验），记随机变量X为n重伯努利试验中A出现的次数，则X～B（n，p）.

（3）服从泊松分布的随机变量

设随机变量X的分布律为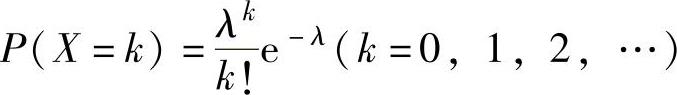，则称X是服从参数为λ

（λ>0）的泊松分布的随机变量，简称X服从参数为λ的泊松分布，记为X～π（λ）.

【典型例题】

例7.4.1 （单项选择题）某人向同一目标独立重复射击，每次命中目标的概率为p（0<p<1），则此人第4次射击恰好是第2次命中目标的概率为（）.

A.3p（1-p）2 B.6p（1-p）2 C.3p²（1-p）2 D.6p²（1-p）2

精解所求概率=P{前3次射击恰有一次命中目标，而第4次射击命中目标}(https://www.chuimin.cn)

=P{前3次射击恰有一次命中目标}·P{第4次射击命中目标}

=P（X=1）·p（其中X表示3次射击过程中命中目标的次数，

X～B（3，p））

=C₃¹p（1-p）2·p=3p²（1-p）2.

因此本题选C.

例7.4.2 从学校回家途中需经过3个信号灯，设在各个路口遇到红灯是相互独立的，

并且概率都为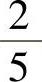，记X为途中遇到红灯的次数，求X的分布律.

精解从学校回家，每经过一个路口可理解为一次试验，它有两个可能的结果，A，A

（其中，A={经路口时遇到红灯}），且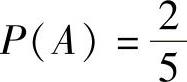，这样经过3个路口可以理解成3重伯努

利试验，于是，从而X的分布律为

即

例7.4.3 设随机变量X～π（λ），且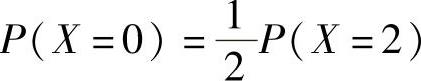，求概率P（X=3）.

精解欲求概率P（X=3），应先确定参数λ（λ>0）.由于X～π（λ），所以由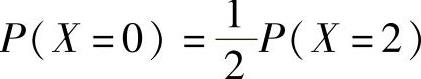得，即λ=2.于是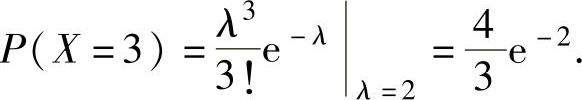

例7.4.4 某射手的命中率为0.75，现对某一目标连续独立射击，直到击中为止.记X为射击终止时的射击次数，求：

（1）X的分布律；

（2）X取偶数值的概率.

精解（1）只要算出概率P（X=n）（n=1，2，…）即可.

由于{X=n}={前n-1次都未命中，而第n次命中}

={前n-1次都未命中}{第n次命中}，

而{前n-1次都未命中}与{第n次命中}独立，所以

P（X=n）=P{前n-1次都未命中}P{第n次命中}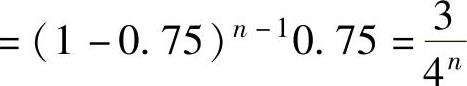，从而X的分布律为（2）P{X取偶数值的概率