在重构问题中，令A old为重构前网络的旧的邻接矩阵，它由上一次优化计算得到。为了使拓扑结构的变化尽可能小，在新的可视性矩阵中，继续保持A old中仍然可用的链路，这就形成了一个由A old退化而形成的残留拓扑A rem。接下来，逐一增加k条链路到A rem中，每一条链路的增加服从所提的边增加算法。接下来，将从候选链路集合A can中逐一增加k个边到残留拓扑A rem中，并使其加权代数连通度最大。表5-2边增加算法伪代码（续表）......
2023-07-02
网络重构中边增加的算法仿真优化方案
【摘要】：从仿真结果中可以看出，提出的边增加算法能够在自由度约束下保持网络的连通性，并使网络在动态状态下保持较高的加权代数连通度。这意味着采用本章提出的算法，每次实施网络重构时仅需调整少数链路即可，大规模地对链路进行调整是没有必要的，同时也反映了边增加算法随k的收敛较快，算法具有实用价值。图5-7边增加算法中不同自由度情况下maxλ2与k的关系
设有一个动态的空间信息网络，其中N=50，d=4，k=30，仿真结果如图5-6所示，为了便于观察，将节点绘制呈圆形分布，实际中的节点是随卫星轨道位置分布的。随着卫星节点的运动，选取了t 0，t 1，t 2 3个时刻（t 0＜t 1＜t 2）的可视性情况作为参考，如图5-6（a），（c），（e）所示。其中，t 0时刻的优化拓扑根据网络初始化中的边移除算法得到，如图5-6（b）所示，其最大化的加权代数连通度maxλ2（t 0）=0.685 1。t 1和t 2时刻的优化拓扑根据边增加算法、当前的可视性矩阵和上一时刻的优化拓扑运算得到，分别如图5-6（d）和（f）所示，其中maxλ2（t 1）=0.359 8，maxλ2（t 2）=0.598 6。从仿真结果中可以看出，提出的边增加算法能够在自由度约束下保持网络的连通性，并使网络在动态状态下保持较高的加权代数连通度。
图5-6 边增加算法性能示例
（a）t 0时刻的可视性状态；（b）t 0时刻的优化拓扑；（c）t 1时刻的可视性状态；（d）t 1时刻的优化拓扑；（e）t 2时刻的可视性状态；（f）t 2时刻的优化拓扑
接下来考察参数k对边增加算法性能的影响。选择规模为N=50的网络，令k=10～60，分别考察d=2，4，6，8，10情况下的优化结果。算法结果如图5-7所示。可以看出，随着k的增加，maxλ2随之增大；但是随着k的持续增加，maxλ2最终趋向稳定，不再有显著提升。本例中，当k≤30时，增加k的数值能够快速地提升maxλ2值，但是当k＞30之后，maxλ2几乎维持不变。这意味着采用本章提出的算法，每次实施网络重构时仅需调整少数链路即可，大规模地对链路进行调整是没有必要的，同时也反映了边增加算法随k的收敛较快，算法具有实用价值。
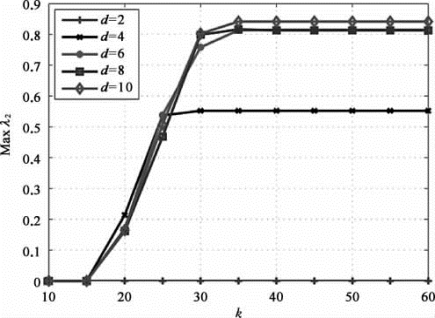
图5-7 边增加算法中不同自由度情况下maxλ2与k的关系
有关空间激光微波混合信息网络技术的文章
- 详细阅读
-
网络初始化中的边移除算法仿真详细阅读
由于穷举算法在网络规模较小时能够得到问题的精确最优解，因此将提出的边移除算法与穷举算法进行对比，建立一个N=6，d=2的模型来对比穷举算法的精确最优解、边移除算法的上限和边移除算法的次优解。而且，穷举算法消耗的计算时间约为边移除算法计算时间的100倍。接下来，为了考察边移除算法的平均性能，随机构建100个拓扑，每个拓扑中均具有5个节点，但可视性矩阵χ和链路开销矩阵C均随机生成。图5-5边移除算法平均性能......
2023-07-02
-
网络初始化问题：边移除算法优化详细阅读
对于网络初始化问题，可以简单地求得其松弛问题的最优解。因此，需要从χ中逐一移除链路，直至其满足整型约束条件。显然，式指出了G′的加权代数连通度的上界。因此，边移除算法的主要思想是每次迭代都从图中移除一条具有最小Δij的边，再对移除后的拓扑进行最优化计算来重新分配链路权重。表5-1边移除算法伪代码（续表）......
2023-07-02
-
社会网络算法的优化方法详细阅读
1）BA网络算法初始设定m0个孤立节点。此算法来自于对分子网络中蛋白质组织结构的分析。研究发现，对于交互和规律的网络来说，高度连接的蛋白质连接被系统的抑制，然而在那些处于高度连接和稀少连接之间的蛋白质结构却没有被抑制。表3-1算法1表3-2算法23）中心分析中心性分析用来检测网络中的关键点以及对网络元素进行排序。......
2023-07-02
-
熔透控制算法优化方案详细阅读
在TIG焊熔透控制系统中，控制器采用的是模糊PID控制方法，这种控制系统在焊接过程中具有自校正控制的功能。熔透控制是在起弧稳定后开始的，为了保证控制的准确性，取前10个周期的熔宽平均值作为整个控制过程的熔宽参考值。根据这些控制规则，再按照模糊控制推理合成规则进行运算，采用最大隶属度方法进行模糊判决，经过多次的试验和修改，得到最终的模糊控制表。......
2023-06-26
-
混沌粒子群优化算法优化方案探究详细阅读
混沌粒子群优化算法的基本思想是采用混沌序列初始化粒子的位置和速度,先对当前粒子群体中的最优粒子进行混沌寻优,然后把混沌寻优的结果随机替换粒子群体中的一个粒子。,z1N),根据式(4-6)得到N个向量z1,z2,…如果粒子适应度优于全局极值gbest,则将gbest设置为新位置。则混沌粒子群优化算法的流程为:初始化,设置最大允许迭代次数或适应误差限,以及CPSO算法的参数惯性权值和学习因子。,PgD)进行混沌优化:将Pgi(i=1,2,…计算其适应值,得到性能最好的可行解pb。......
2023-06-23
-
群体智能算法优化方案详细阅读
智力激励法是运用群体创造原理，充分发挥集体创造力来解决问题的一种创新设计方法。其中最常用的是书面集智法，即以笔代口的默写式智力激励法。函询集智法有两个特点，也是其优点。......
2023-06-26
-
系统仿真的概述及优化方案详细阅读
目前系统仿真作为研究、分析和设计系统的一种有效技术正被广泛应用。当系统比较复杂尤其是引进非线性因素后，此微分方程经常不可求解，所以采用仿真方法求解。连续系统计算机仿真的中心问题是将微分方程描述的系统转变为能在计算机上运行的模型。离散事件系统模型可以进一步分为动态和静态两类。图7-3 离散事件系统的仿真步骤......
2023-07-15
相关推荐