金属的锻造性能是衡量金属材料利用锻压加工方法成形的难易程度，是金属的工艺性能指标之一。金属的锻造性能常用金属的塑性和变形抗力这两个指标来衡量。合金钢中合金元素的含量增多，锻造性能变差。金属组织内部有缺陷，如铸锭内部有缩松、气孔等缺陷，将引起金属的塑性下降，锻造时易出现断裂等现象。......
2023-06-28
仿真设计及性能分析优化方案
【摘要】：图9-17未调度任务优先级之和比较图9-18总能耗比较图9-19任务调度完成时刻比较由图9-17、图9-18、图9-19可知，在选取的6个仿真场景中，MNSGA-Ⅱ对于目标函数f 1，f 2和f 3的优化效果均优于MOGA，其中未调度任务优先级权值之和的平均值降低了66.77%，总能耗平均值降低了69.73%，任务调度完成用时平均值降低了35.27%。
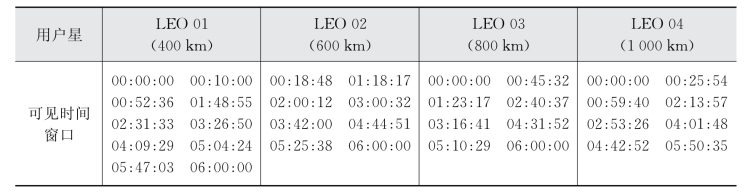
采用9.4.3节中继卫星系统作为仿真场景进行混合链路资源调度问题的优化求解，其中中继星定位与东经10°上空，星上天线终端具体参数如表9-3所示，用户星的轨道参数如表9-4所示，仿真时段为00∶00∶00～06∶00∶00，中继卫星与用户星间的可见时间窗口可由STK仿真得到，如表9-6所示。
表9-6 用户星可见时间窗口
1）算法收敛特性
多目标进化算法可以同时对模型中多个目标函数进行优化，其优化求解的主要目标是不断逼近问题Pareto解的最优前沿，算法收敛情况作为评价一个算法性能的重要衡量指标，直接影响算法运行结果的优劣。以任务量为64时的仿真场景为例，在仿真试验中记录了每一代种群个体中目标函数的最优值，其中遗传进化过程中f 1，f 2和f 3的最优值曲线如图9-16中（a）～（c）所示，Pareto解最优前沿如图9-16中（d）所示。
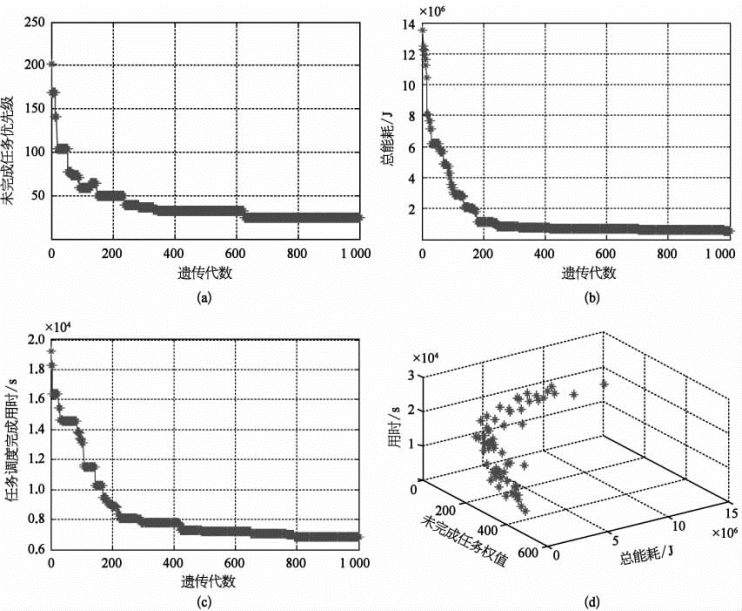
图9-16 各优化目标收敛曲线及Pareto解最优前沿
（a）目标函数f 1收敛曲线；（b）目标函数f 2收敛曲线；（c）目标函数f 3收敛曲线；（d）非支配解最优前沿
图9-16中最优值收敛曲线（a）～（c）中，f 1，f 2和f 3在前200代进化时快速收敛，同时在基本收敛之后，仍能够跳出局部最优值，扩大搜索范围进一步寻找更优解，因而在进化后期存在进一步寻优过程，表明MNSGA-Ⅱ算法能够保持种群多样性，避免算法陷入局部最优。由图9-16中优化结果的Pareto最优前沿可知，f 1未完成任务优先级与f 2总能耗、f 2调度完成用时均成反比，最优前沿上的每一个点都是Pareto最优解，在不同的能耗和调度时间约束条件下，都能够满足决策者的要求，最终决策者只需根据各优化目标的相应偏重值，从Pareto最优解集中选择一个或者一组“足够满意”解作为资源调度问题的最终结果即可。
2）调度优化性能
以任务量为32，48，64，80，96，112的仿真场景为例，图9-17、图9-18、图9-19给出了调度结果中3个目标函数的优化效果，在不同的任务规模条件下进行多次仿真运算，记录了最优值、最劣解并计算优化结果平均值，同时比较了本算法优化结果与多目标遗传算法（MOGA）的优化结果。
图9-17 未调度任务优先级之和比较
图9-18 总能耗比较
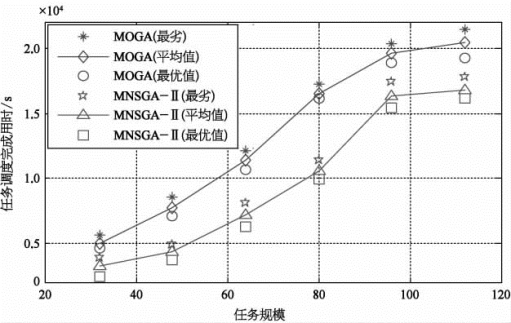
图9-19 任务调度完成时刻比较
由图9-17、图9-18、图9-19可知，在选取的6个仿真场景中，MNSGA-Ⅱ对于目标函数f 1，f 2和f 3的优化效果均优于MOGA，其中未调度任务优先级权值之和的平均值降低了66.77%，总能耗平均值降低了69.73%，任务调度完成用时平均值降低了35.27%。在本MNSGA-Ⅱ算法中，由于设计了自适应交叉、变异算子和具有精英保留策略的选择算子，扩大算法搜索空间的同时保证了Pareto解搜索的多样性，而每一代种群内的优秀个体总能够通过精英保留策略转入下一代，从而保证算法的快速收敛。
由图9-17、图9-18、图9-19中的3个目标函数优化效果曲线可知，通过MNSGA-Ⅱ和MOGA求解得到的调度结果中，f 1未调度任务优先级之和随任务量增加而呈线性增长趋势；f 2总能耗在任务量较少时增长幅度较小，在任务量达到96及以上时大幅度增长；而f 3任务调度完成用时的增长情况则相反，在任务量较少时持续增长，而当任务量达96个以上时增长趋于平缓。这是由于在中继卫星系统中可见时间窗口的约束下，相同场景内的总窗口时间已根据调度时间段确定，而终端天线利用率随着任务量的增大而接近饱和，由于算法优化过程中优先选取光学天线进行任务传输，当任务量达80个时，光学天线上安排的最后一个任务的传输结束时刻也逼近调度总时间的结束时刻，即光学天线中继能力已基本接近饱和，天线资源利用率达到最大值。此时再增大任务量，后续任务将选用微波天线终端进行传输，因而调度结果中f 1与f 2数值持续增长，而任务完成总用时基本不变。由于激光终端总能耗远远低于微波终端，因此总能耗在任务规模较小时增长平缓，而在规模较大时呈快速增长趋势。且由于微波链路传输能力有限，随着任务规模增大，未调度任务量增长幅度呈增大趋势。
在实际调度过程中，通过上述多目标优化算法获得Pareto最优解集后，决策者从最优解集中选择一个适合当前应用情况的最优解作为资源调度最终方案，以此为依据，调度中心向中继星和用户星发送相应的控制指令来指导系统接入，完成整个资源调度过程。针对在不同的实际应用需求下，决策者对调度模型中目标函数的侧重不同的情况，MNSGA-Ⅱ算法可以提供尽可能多的最优解集，为决策者选择适合当前实际情况的最终调度方案提供便利，保证不同应用需求下的调度结果总是当前应用情况下的最优方案，从而实现中继卫星资源的有效合理利用。
有关空间激光微波混合信息网络技术的文章
- 详细阅读
-
仿真实验及结果分析优化方案详细阅读
图9-34比较了在不同任务规模下两种算法优化结果中的续传次数，MACA算法中的续传次数要低于NSGA-Ⅱ算法，平均减少了25.1%。图9-35是两种算法优化结果的资源负载失衡度，MACA算法与NSGA-Ⅱ算法结果相当，两算法的负载失衡度均在0.01以下。对本章场景仿真实验，分别得到整传调度和续传调度结果如图9-36和图9-37所示。......
2023-07-02
-
电路设计与仿真模拟工具优化方案详细阅读
电路设计及仿真模拟的传统工具主要有Cadence公司的Spectre、SYNOPSYS公司的HSPICE以及Mentor公司的Eldo三大类。尤其是其具有图形界面的电路图输入方式，使其成为目前最为常用的CMOS模拟集成电路设计工具。与Cadence公司的Spectre图形界面输入不同，HSPICE通过读取电路网表以及电路控制语句的方式进行仿真，是目前公认仿真精度最高的模拟集成电路设计工具。Eldo可以方便地嵌入到目前的其他的模拟集成电路设计环境中，并可以扩展到混合仿真平台ADMS，进行数字、模拟混合仿真。......
2023-06-26
-
生成刀路轨迹及仿真优化方案详细阅读
Stage1.生成刀路轨迹Step1.进入区域切削模式。图3.5.10 “区域切削模式”对话框（一）注意：加工区域在“区域切削模式”对话框（一）中排列的顺序与选取切削区域时的顺序一致。此时“区域切削模式”对话框如图3.5.16所示，在下拉列表中选择选项，图形区中显示所有加工区域正投影方向下的刀路轨迹，如图3.5.17所示。图3.5.15 “往复切削参数”对话框图3.5.16 “区域切削模式”对话框（二）Step3.生成刀路轨迹。......
2023-06-18
-
垫设计及优化方案详细阅读
12.3.5.1 衬板1.衬板1（图12-139）图12-139 衬板1（图12-135的件号99）2.衬板2（图12-140）图12-140 衬板2（图12-135的件号13）3．衬板3（图12-141）图12-141 衬板3（图12-135的件号43）12.3.5.2 凸模固定板垫板1.凸模固定板垫板1（图12-142）图12-142 凸模固定板垫板1（图12-135的件号98）2.凸模固定板......
2023-06-26
- 详细阅读
-
系统仿真的概述及优化方案详细阅读
目前系统仿真作为研究、分析和设计系统的一种有效技术正被广泛应用。当系统比较复杂尤其是引进非线性因素后，此微分方程经常不可求解，所以采用仿真方法求解。连续系统计算机仿真的中心问题是将微分方程描述的系统转变为能在计算机上运行的模型。离散事件系统模型可以进一步分为动态和静态两类。图7-3 离散事件系统的仿真步骤......
2023-07-15
- 详细阅读
相关推荐