1．定子各相绕组的自感系数以a相为例来讨论定子绕组自感系数的变化。2．定子各相绕组间的互感系数和自感系数的情况类似，凸极机的定子绕组互感也是随着转子转动呈周期性的变化，其周期也是π。以Mab为例讨论定子绕组间互感系数的变化。由于a、b两绕组在空间相差120°，a相绕组的正磁通交链到b相绕组总是负磁通，即定子绕组间的互感系数恒为负值。......
2025-09-29
复式河槽阻力系数分析
【摘要】：该研究表明:9.3.1.2阻力系数阻力系数在估算复式河槽过流能力、平均流速和确定垂线平均流速横向分布等方面起着重要作用。在光滑复式河槽中，滩槽局部阻力系数基本上为常数，但大小不同。对于滩槽粗糙不同的或非对称的复式河槽，滩地的局部阻力系数不再保持不变。对于所有系列而言，滩槽局部阻力系数都将随着相对水深的增加而减小。
9.3.1.1 漫滩河道紊流横向扩散特性
复式河道是天然河流中常见的河流类型，其水流泥沙运动与单一河道明显不同。当水流由主槽漫入边滩后，不仅是过流断面发生了改变，而且水流流态也发生了改变。复式河道水流具有明显的三维特性，各种水流参数(如流速、切力、扩散系数等)均随空间位置不同而各异。通常，实际应用时，更关心的是这些参数沿边界和横向的变化(断面形态如图9-10所示)。刘兴年和Knight(2000)，Liu et al. (1999)引用了大量的SERC—FCF(英国科学工程研究会洪水水槽)试验资料分析了漫滩河道紊流横向扩散特性。
1.单一河道紊流扩散系数的横向变化
在单一河槽中，河道紊流扩散系数是水流平均流速u、水深h、水面宽度w、摩阻流速u、水密度ρ和粘性系数μ 的函数，可表示为:
通过量纲分析得:
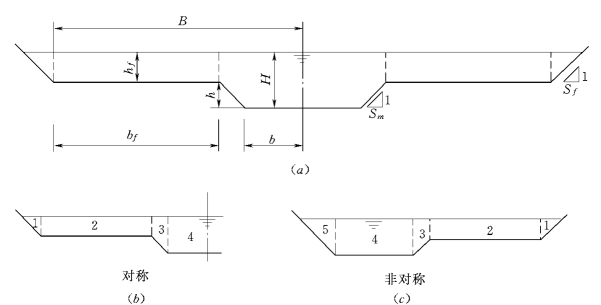
图9-10 复式河槽断面形态及区域分划
图9-11 无量纲紊流扩散系数ε/(uh)和相对宽度、阻力系数的关系
2.漫滩河道紊流扩散系数的横向变化试验成果
试验在英国HR WALLINGFORD、伯明翰大学和四川大学进行，水槽宽度2m 和10m。水深0.1～0.7m，相对水深0.05～0.5。紊流扩散系数:
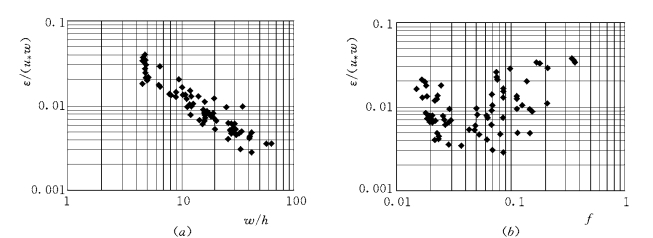
图9-12 无量纲紊流扩散系数ε/(uw)和相对宽度、阻力系数的关系
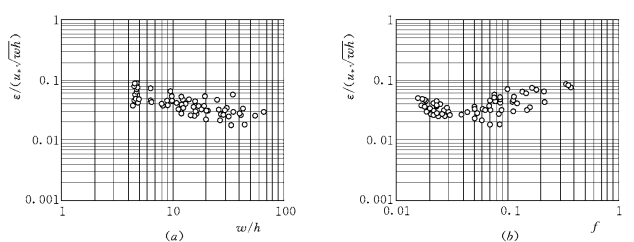
图9-13 无量纲紊流扩散系数ε/(uwh)和相对宽度、阻力系数的关系
根据试验资料，点绘漫滩河道紊流扩散系数的横向变化，如图9-14所示。由此可见，当相对水深Dr=(H-h)/H 较小时，漫滩部分的紊流扩散系数比主槽大得多。随着相对水深加大，漫滩与主槽的紊流扩散系数渐渐接近。主槽水流紊流扩散系数和相对水深的关系，近乎为常数0.07。(https://www.chuimin.cn)
3.漫滩河道相对宽度、深度对紊流扩散系数的横向变化的影响
9.3.1.2 阻力系数
阻力系数在估算复式河槽过流能力、平均流速和确定垂线平均流速横向分布等方面起着重要作用。Yang et al. (2005)通过分析SERC-FCF的大量的试验资料 (其断面形态如图9-10所示)，建立了达西—韦斯巴赫综合阻力系数、局部阻力系数及曼宁系数与不同断面形态、不同床面粗糙度的关系，并分析了传统方法不能正确估算过流能力的原因在于:传统方法忽略了滩槽交界面的表观切应力(其实质是增大了附加阻力)。该研究表明:
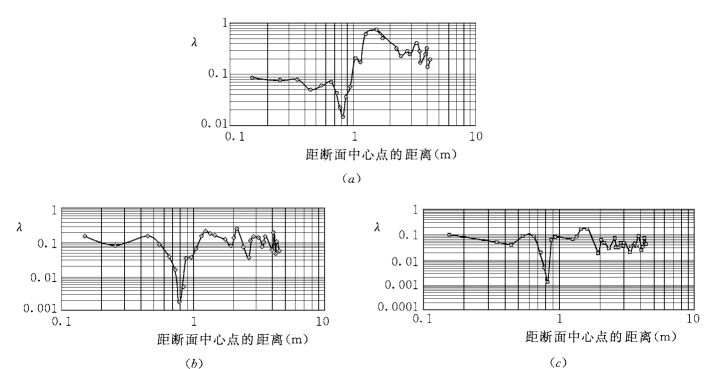
图9-14 漫滩河道紊流扩散系数的横向变化
(a)SERC-FCF 010201(Dr=0.10 和B/b=6.67);(b)SERC-FCF 010401(Dr=0.2 和B/b=6.67);
(c)SERC-FCF 010601(Dr=0.2 和B/b=6.67)
(1)复式河槽达西—韦斯巴赫局部阻力系数与滩槽宽度比、主槽边坡、对称性、滩地粗糙度等有关。在光滑复式河槽中，滩槽局部阻力系数基本上为常数，但大小不同。对于滩槽粗糙不同的或非对称的复式河槽，滩地的局部阻力系数不再保持不变。对于所有系列而言，滩槽局部阻力系数都将随着相对水深的增加而减小。
(2)二次流将影响垂线平均流速及床面剪切应力的横向分布，如图9-15所示。如果忽略二次流，滩槽床面平均剪切应力相对误差分别为17.6%、15.3%;如果考虑二次流，则滩槽相滩误差的平均值将减至4.4%与4.3% (Liu et al.，2005c)。
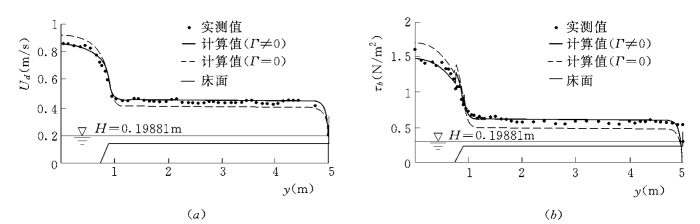
图9-15 二次流对垂线平均流速及床面剪应力横向分布的影响(阻力系数采用实测值，λi均取0.13，SERC-FCF 010501)
(a)垂线平均流速横向分布;(b)床面剪切应力横向分布
(3)复式河槽滩地、主槽曼宁阻力系数也分别与滩槽宽度比、主槽边坡、对称性、滩槽床面粗糙差别等有关。对于所有系列而言，基本上存在相同的变化趋势:滩地糙率(nf)、综合糙率(nc)都是先随着相对水深的增加而减小，后随着相对水深的增加而增大;而主槽糙率(nm)变化趋势则相反。与床面粗糙度相同的单一河槽相比，基本上是复式河槽的滩地曼宁阻力系数比单一河槽的小，而主槽的比单一河槽的大，如图9-16所示。
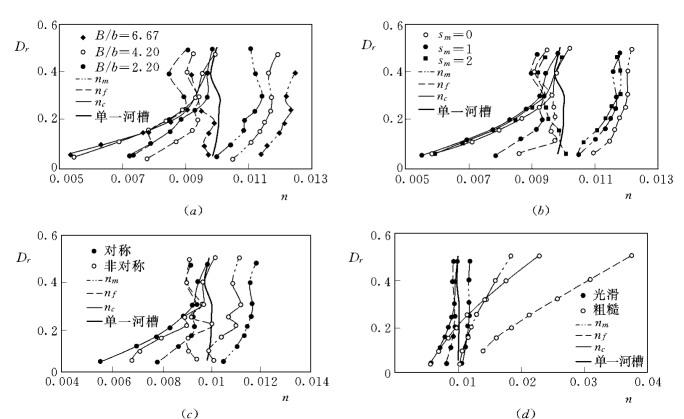
图9-16 曼宁阻力系数受相对水深、滩槽宽度、主槽边坡、光滑与粗糙复式河槽等的影响
(a)曼宁阻力系数随相对水深和滩槽宽度比的变化;(b)主槽边坡对曼宁阻力系数的影响;(c)非对称性对曼宁系数的影响;(d)光滑与粗糙复式河槽的曼宁阻力系数随相对水深的变化
9.3.1.3 复式河槽阻力系数
SERC-FCF的试验资料表明尽管断面形态不同，但主槽区[即图9-10 (b)的区域4]平均Darcy-Weisbach 阻力系数f4，随相对水深的变化趋势是相似的，如图9-17(a)。当Dr＜0.25，f4随着相对水深的增加而增加。当Dr＞0.25时，f4的变化趋势却相反，即随着相对水深的增加而减小。因此，主槽区Darcy-Weisbach 阻力系数f4，与相对水深为Dr=0.25时的阻力系数f4(0.25)的比值遵循某种关系。图9-17 (b)表明对于SERC-FCF 的试验资料而言，它们的比值满足抛物线分布。图9-17 (c)表明，对于所有不同的断面形态，滩槽平均阻力系数之比与相对水深有关，均随着相对水深的增加而减小(杨克君等，2005b)。
相关文章
- 详细阅读
-
散热系数的计算方法和影响因素：Nul数、导热详细阅读
在自由对流条件，对流散热系数可按式计算式中 Nul——努基尔数；λ——空气的导热系数；l——空气流过表面的长度。表5-3 公式中长度c、n和长度l的选择对流散热系数α是温度的函数，它随温度而变化。在热分析时，为了与对流散热的形式一致，将辐射散热通过表面散热系数简化为公式所示。因此，外表面的散热系数为α=αcon+αrad......
2025-09-29
-
界面反应系数的原子模型优化方案详细阅读
在3.2.4节的动力学分析中，最重要的两个动力学参数是原子扩散率和界面反应控制系数。为了方便比较，在界面反应控制系数中我们提出了一个类似的表达式。图3.11描述了越过Cu6Sn5/Sn界面的活化能，其中ΔGm是穿过界面的迁移活化能，ΔG是反应中或者是Cu6Sn5生长中每一个原子对应的化合物的自由能增益（驱动力），而λ是界面的宽度。图3.11越过Cu6Sn5/Sn界面的活化能式中，p为压力。但由于界面反应过程极其缓慢，因此不太可能考虑分子生长。......
2025-09-29
-
极限应力、许用应力与安全系数总结详细阅读
构件失效前所能承受的最大应力称为极限应力或危险应力，用σ0 表示。考虑到载荷估计的准确程度、应力计算方法的精确程度、材料的均匀程度以及构件的重要性等因素，为了保证构件安全可靠地工作，应使它的最大工作应力小于材料的极限应力，使构件具有适当的强度储备。一般把极限应力除以大于1 的安全因数n，作为设计时应力的最大允许值，称为许用应力，用[σ] 表示。......
2025-09-29
-
电阻的温度系数和噪声对电路产生的影响详细阅读
温度系数：以25℃作为标准温度,当温度变化1℃时,电阻值的变化量为d R,则有：图6166 制作流程图01 使用“矩形工具”绘制矩形如图6167所示。式中,α为温度系数；R25为温度在25℃时的电阻值；d T为温度的变化量。电阻器噪声将会对电路信号产生一定干扰。如4k7的含义是电阻器的阻值为4.7 kΩ,允许误差为10%。附图2电阻的色环标记法色环所表示的含义见附表5。......
2025-09-29
-
容许应力和安全系数的优化设计方案详细阅读
在理想情况下，为了保证构件能正常工作，必须使构件在工作时产生的工作应力不超过材料的极限应力。即构件中的最大工作应力不超过某一限值，将极限应力σ0缩小K倍，作为衡量材料承载能力的依据，称为允许应力，用[σ]表示，即式中 K——一个大于1的系数，称为安全系数。安全系数K的确定相当重要又比较复杂。一般工程中规定脆性材料Kb＝2.5～3.0塑性材料或Ks＝1.4～1.7常用材料的许用应力可见表5-2。表5-2常用材料的许用应力......
2025-09-29
-
力法典型方程与柔度系数计算方法详细阅读
根据叠加原理，式可写成以下形式：图14-12位移条件式就是为求解多余未知力X1和X2所需要建立的力法方程。对于高次超静定问题，其力法方程也可类似推出。当原结构在去掉多余约束处的已知位移为零时，其力法方程为方程中的系数称为柔度系数，位于主对角线上的系数δii称为主系数，在主对角线两侧的系数δij称为副系数，Δ1P称为自由项。由于基本体系是静定的，所以力法方程中各系数和自由项都可以按照上一单元位移计算的方法求出。......
2025-09-29
-
实验方法及结果分析详细阅读
实验中触头预压力FK保持为25.1N。表6-5为两组实验和仿真的详细结果数据。图6-21为峰值电流为11.3kA时的电流和电动斥力实验波形。表6-5 实验和仿真结果比较在仿真中，表征触头接触情况的参数ξ取值为0.45。而电流峰值为9.0和11.3kA时，对应的触头压力分别为35.4和55.9N。根据式（6-1），可得导电斑点的半径分别为0.158和0.199mm。因此，引入导电桥模型，采用有限元静态分析的方法计算电动斥力是合理的，也是有效的。......
2025-09-29
相关推荐