微分几何第4讲：改进的定理

2023-11-23 理论教育版权反馈

【摘要】：本讲内容是上一讲定理的一个改进．先介绍一些引理．引理1设A1，A2是两个n×n实对称矩阵，已知Sj＝N，j＝1，2，以及S1＝S2，则证明由上一讲引理2，知上式两端都加上，则引理1成立．下面研究三个或三个以上n×n实对称矩阵A1，A2，…

本讲内容是上一讲定理的一个改进．

先介绍一些引理．

引理1　设A1，A2是两个n×n实对称矩阵，已知Sj＝N（Aj），j＝1，2，以及S1＝S2，则

证明　由上一讲引理2，知

上式两端都加上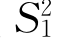 pagenumber_ebook=59,pagenumber_book=51 ，则引理1成立．

下面研究三个或三个以上n×n实对称矩阵A1，A2，…，Ap的情况，这里正整数p≥3．记Sj＝N（Aj），1≤j≤p．设S1＝S2＝…＝Sp＞0．记Aα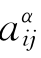＝（ pagenumber_ebook=59,pagenumber_book=51 ），1≤α≤p，1≤i，j≤n．令

由于不等式（1．4．3）左、右两端在正交变换下不变，先经过一个适当的正交变换，使得A1变为一个实对角矩阵，不妨仍记为A1，即可设

矩阵（A1Aα－AαA1）的第i行，第j列元素

我们有下述一系列的估计．

引理2　对任意α∈｛2，3，…，p｝，如果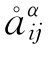｛ pagenumber_ebook=60,pagenumber_book=52 ，1≤i＜j≤n｝中至少有两个元素非零，则

由引理1和引理5，立刻可得引理6中不等式．由上面的推导过程以及上一讲引理2，可以知道等号成立的条件是显然的．

与前面一样，设，S1＝max｛S1，S2，…，Sp｝，S1是一个正常数b．

考虑函数

现在证明下一个引理．

引理7　如果存在α∈｛2，…，p｝，使得在点q， pagenumber_ebook=69,pagenumber_book=61 ∈（0，b），则

注：这里字母上加一小圈表示相应量在点q取值．

证明　为方便，不妨设α＝2，由于（1．4．63）右端及引理7要证明的等式在一个实正交矩阵变换下不变，因此可设

引理7的结论成立．

现在证明本讲最后一个引理．(www.chuimin.cn)

当上式等号成立时，或者A1，A2，…，Ap全为零矩阵，或者A1，A2，…，Ap中只有两个矩阵是非零矩阵．在后一种情况下，不妨设仅A1，A2不是零矩阵，这时有S1＝S2，并且存在n×n实正交矩阵T，满足

由（1．4．77）和（1．4．79），有

由于F在点q取到最大值，因而在M的每一点上，有

从推导过程可知等号成立的条件是显然的．

由第3讲公式（1．3．28）和（1．3．66），有

令矩阵Aα＝Hn＋α，1≤α≤p，再利用引理8的结论，有

应用（1．4．83）于（1．4．82），有

利用M是Sn＋p（1）内闭子流形，上式左端在M上积分为零．而上式右端第一大项在M上积分必非负．那么，可以得到

于是，有下述定理．

定理3（李安民、李济民）　设M是球面Sn＋p（1）内闭极小等距浸入子流形，这里p≥2，又设在Sn＋p（1）内，M的第二基本形式长度平方S≤，则或者S恒等于零，M是全测地的；或者S恒等于，M是S4（1）内的Veronese曲面．

利用定理条件，必有

由（1．4．85）和（1．4．86）知，在M上处处有

或者S恒等于零；当S不恒等于零时，在S不等于零的M点上，必有S恒等于常数．容易明白，S不恒等于零的M的点集既是M的开集，又是M的闭集．又M连通，则在M上处处有S＝其余结论从上一讲可以知道．

编者的话

本讲内容取自李安民、李济民在1992年发表的一篇文章．由于当p≥2时，

在p≥2时，这篇文章改进了上一讲的定理．

［1］Li Anmin and Li Jimin．An intrinsic rigidity theorem for minimal submanifolds in a sphere，Arch．Math．，Vol．58（1992）：582-594．