微分几何第5讲：广义最大值原理

2023-11-23 理论教育版权反馈

【摘要】：我们知道，紧流形上的光滑函数有最大值．那么，对于完备Riemann流形呢？，en，沿测地线ρ，en＝，这里s是这测地线的弧长．M的互相垂直的单位切向量场e1，e2，…，en－1沿ρ是平行移动的．记是沿测地线ρ的Jacobi场，满足＝0，＝ei，这里为方便，沿测地线ρ的ei简记为ei．利用公式和，在r的可微分点，在r＞0的点及不在点P的割迹之内，r是光滑的（什么是割迹呢？

我们知道，紧流形上的光滑函数有最大值．那么，对于完备Riemann流形呢？本讲考虑这个问题．

由［1］第一章定理7可以知道，当φ（s）＞0（0≤s≤r，r是一个正常数）时，二阶线性常微分方程

有唯一解f（s），且当0＜s＜r时，0＜f（s）＜1，是一个单调递增函数．设M是一个完备连通的n维Riemann流形．ρ：［0，r］→M是一条以弧长s为参数的测地线．ρ（0）＝P，ρ（r）＝x．即这条测地线以点P为起点，以点x为终点．在本讲，正整数n≥2．

由［2］的§5，§6可以知道，距离函数r沿M在点x的切向量X方向的Hessian矩阵（X要求垂直于这条测地线在点x的切向量）

这里〈，〉表示M的Riemann内积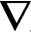， pagenumber_ebook=75,pagenumber_book=67 是M的Riemann联络（又称协变导数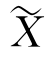），是沿ρ（［0，r］）的Jacobi场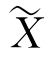．在点P是零向量，在点x是向量X（与［2］内§5，§6唯一不同之处是本讲的曲率的定义与［2］中恰相差一个符号．许多文章及书籍中曲率的定义都可能彼此相差一个符号（指正、负号），读者千万要小心）．

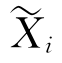同前几讲一样，记Δ是M上Laplace算子．在M内选择局部正交标架场e1，e2，…，en，沿测地线ρ（［0，r］），en＝，这里s是这测地线的弧长．M的互相垂直的单位切向量场e1，e2，…，en－1沿ρ（［0，r］）是平行移动的．记 pagenumber_ebook=75,pagenumber_book=67 （s）是沿测地线ρ（［0，r］）的Jacobi场（1≤i≤n－1），满足（0）＝0，（r）＝ei（r），这里为方便，沿测地线ρ（［0，r］）的ei（ρ（s））简记为ei（s）．利用公式（1．5．2）和（1．5．3），在r的可微分点（这里r作为从点P出发的距离函数），在r＞0的点及不在点P的割迹之内，r是光滑的（什么是割迹呢？设r（s）是M内一条测地线，这里s是r的弧长参数．如果存在一个正常数s0，∀s∈［0，s0］，测地线r（s）是连接两点r（0）与r（s0）的最短测地线，即在M内连接这两点r（0）与r（s0）的所有逐段光滑曲线中，以r（s）的长度为最短．但对∀s*＞s0，在M内连接两点r（0）与r（s*）的所有逐段光滑曲线中，r（s）并不是长度最短的测地线，这样的点r（s0）称为r关于r（0）的割点．记P＝r（0），当点P固定时，M在点P的切空间Tp（M）内向量s0 pagenumber_ebook=75,pagenumber_book=67 的终点（以点r（0）（点P）为起点）称为r的切割点．当测地线r（s）在所有以同一点P为起点的、以弧长s为参数的测地线集合中变动时（当变动时，r（s）变动），r的所有割点全体组合的集合称为点P的割迹．TP（M）中相应的切割点全体组成的集合称为点P的切割迹．参考［2］§10），有

这里f（s）是满足方程组（1．5．1）的一个光滑解，那么，有

如果沿这条测地线ρ（［0，r］），没有点P的割点，利用Jacobi场的极小性性质（［2］第7节），有

其中K（ei（s），en（s））（1≤i≤n－1）是M在点ρ（s）由ei（s）和en（s）张成的截面曲率（所有文章和书籍的截面曲率的定义完全一样），Ric（en（s），en（s））是M在点ρ（s）沿en（s）方向的Ricci曲率．

利用公式（1．5．1）和分部积分，有

先证明一个引理．

引理1　设M是一个n维非紧的完备连通Riemann流形，P是M上一个固定点．设r是M上从点P出发的距离函数．设M的Ricci曲率满足，这里光滑函数φ（r）是一个正的函数，且处处非负，那么，在函数r的可微分点上，有

证明　利用引理条件，知道

将（1．5．8）和（1．5．9）代入公式（1．5．7），在r的可微分点，有

其中C是一个待定正常数，s∈［0，r］．

记

由方程（1．5．1）知道，f（s）不是一个常值函数．由于f（0）＝0，以及当0＜s＜r时，0＜f（s）＜1，有a＞0（显然a≥0，但当a＝0时，f（s）必是一个零函数，矛盾）．

分三种情况讨论：

①如果F（s）在s＝0处达到最大值，有

②如果F（s）在s＝r处达到最大值，有

由上式，有

推论　当φ（r）＝（n－1）k2时（这里k是一个正常数），由上式可知，在r的可微分点，有

不等式（1．5．29）是著名的不等式（［3］第一章）．引理1中φ（r）的光滑性仅需C1就可以了．

设f是非紧完备n维连通Riemann流形M上有上界的C∞函数．不失一般性，假设在一点P∈M，f（P）＝0（否则可考虑函数f（x）－f（P）代替原先考虑的f（x））．又设∀x∈M，f（x）＜sup f，这里sup f是f的正的（有限）上确界．

引入一族函数

这里k是正整数，r（x）是由点P出发的距离函数．Fk（r（x））是r（x）的待定C2正函数族，满足下述条件：

由于函数gk在点xk有最大值，上式是不可能成立的，因此有引理2的第一个结论．对第二个结论，也利用反证法．如果sup｛f（xk）|k∈N｝＜sup f，那么能找到一个δ＞0，以及一点x*∈M，使得对于很大的正整数k，有(www.chuimin.cn)

这与函数gk在点xk有最大值又矛盾．

下面证明

定理4　（非紧完备Riemann流形上最大值原理）

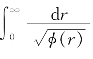设M是n维（n≥2）非紧完备连通Riemann流形，P是M上一个固定点．设M的Ricci曲率，这里r是M上从点P出发的距离函数，φ（r）是一个单调递增的正的C1函数，满足 pagenumber_ebook=81,pagenumber_book=73 ＝∞．那么，对于M上任意有上界的C2函数f，在M上有一点列｛xk|k∈N｝，满足

证明　如果M上存在一点x0，满足f（x0）＝sup f，定理结论成立．下面设∀x∈M，f（x）＜sup f．依照前面叙述，引入函数族gk（x）（见公式（1．5．30），以及Fk（r（x））满足的四个条件），设gk（x）在点xk有最大值．先设点xk不在点P的割迹上．于是，有

由公式（1．5．30），可以得到（下面为简便，省略自变量）

在点xk，利用（1．5．40）的第一式及（1．5．41）的第一式，有

如果xk位于点P的割迹内，设L是从点P到点xk的一条极小测地线，L的长度是r．能够找到L上点q，q在点P邻近，记d（P，q）＝ε，这里ε充分小，ρε是从点q出发的距离函数．∀x∈M，有

这里再重申，r（x）是从点P出发的距离函数．∀δ＞0，取定δ暂不变动．

其次，选择上述ε＞0，使得

这里点x位于以点P为球心、以r＋δ为半径的一个测地球内＝r（x），在含xk的一个小邻域内，ρε关于xk是光滑的，即xk不在点q的割迹内．完全类似Δr的估计，可以看到

这里当r固定时，B是一个正常数．有兴趣的读者可作为一个习题证明上式．

令

那么，可以知道

对于函数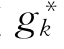 pagenumber_ebook=85,pagenumber_book=77 ，在点xk，估计它的最大值，这里（0）＞0和＝1代替了本讲前述四个条件中的条件（1）．类似前面的估计，先令ε→0，然后令δ→0，最后令k→∞，有与（1．5．57）相同的结果．有兴趣的读者可以仔细地将其写出来．

推论1　取φ（r）＝（n－1）k2，这里k是一个正常数，这恰是1976年丘成桐教授得到的最大值原理（［3］）．

推论2　取φ（r）＝C［1＋（r＋1）2 ln2（2＋r）］，这里C是一个正常数，这恰是忻元龙教授和陈群合作得到的结果（［4］）．

编者的话

这一讲是笔者1993年发表于《数学年刊》的一篇文章的主要定理（［5］）．这篇文章的主要思想来自上述提及的文章［3］．

参考文献

［1］Protter，M．H．，Weinberger，H．F．．Maximum Principle in Differential Equations．Prentice Hall，1967．（有中译本）．

［2］伍鸿熙，沈纯理，虞言林．黎曼几何初步．北京大学出版社，1989．

［3］S．T．Yau．Harmonic function on complete Riemannian manifolds，Comm．Pure．Appl．Math．（1975）：201-228．

［4］Chen，Q．，Xin，Y．L．．A generalized maximum principle and its applications in geometry．Amer．J．Math．，114（1992）：355-366．

微分几何第5讲：广义最大值原理

相关推荐