设n阶矩阵A，若存在n阶可逆矩阵P，使得P－1AP＝Λ，其中Λ 是对角矩阵，则称A可相似对角化，记A～Λ，称Λ 是A 的相似标准形.于是可知，若A可相似对角化，即P－1AP＝Λ，其中P可逆，等式两边同时左乘P，有AP＝PΛ，记由P可逆，则ξ1，ξ2，…＝λn＝0，A的特征值全是零.若A能与对角矩阵Λ 相似，则Λ 的主对角线元素为A......
2023-11-21
张宇线性代数9讲：判断相关性的7大定理
【摘要】：，αn（n≥2）线性相关，则存在n 个不全为零的数k1，k2，…，αn 线性表示的表示法唯一.定理3 如果向量组β1，β2，…，αn 线性相关有非零解.仿定理4的研究方法，便有下面所给的定理5.定理5 向量β可由向量组α1，α2，…，αm 线性无关，则其任一部分向量组也线性无关.总之，向量组部分线性相关，则整体也线性相关；整体线性无关，则任一部分也线性无关.定理7 如果一组n维向量α1，α2，…
定理1 向量组α1，α2，…，αn（n≥2）线性相关的充要条件是向量组中至少有一个向量可由其余的n－1个向量线性表出.
【注】证 先证必要性.设向量组α1，α2，…，αn（n≥2）线性相关，则存在n 个不全为零的数k1，k2，…，kn，使
k1α1＋k2α2＋…＋knαn＝0.
不妨设k1≠0，于是由向量的线性运算规则得
再证充分性.不妨设α1 可用α2，α3，…，αn 线性表示，即
α1＝l2α2＋l3α3＋…＋lnαn，
于是有
1α1－l2α2－l3α3－…－lnαn＝0，
显然1，－l2，－l3，…，－ln 不全为零，故α1，α2，…，αn 线性相关.
其逆否命题：向量组α1，α2，…，αn（n≥2）线性无关的充要条件是α1，α2，…，αn 中任一向量都不能由其余的n－1个向量线性表出.
定理2 若向量组α1，α2，…，αn 线性无关，而β，α1，α2，…，αn 线性相关，则β可由α1，α2，…，αn 线性表示，且表示法唯一.
【注】证 因为β，α1，α2，…，αn 线性相关，所以存在不全为零的数k，k1，k2，…，kn，使得
kβ＋k1α1＋k2α2＋…＋knαn＝0，
其中k≠0（如果k＝0，则由α1，α2，…，αn 线性无关又得k1，k2，…，kn 必须全为零，这与k，k1，k2，…，kn 不全为零矛盾），于是β可由α1，α2，…，αn 线性表示为
再证表示法唯一，设有两种表示法，
β＝l1α1＋l2α2＋…＋lnαn
＝h1α1＋h2α2＋…＋hnαn，
于是
（l1－h1）α1＋（l2－h2）α2＋…＋（ln－hn）αn＝0.
由于α1，α2，…，αn 线性无关，所以必有
li－hi＝0，即li＝hi，i＝1，2，…，n，
故β由α1，α2，…，αn 线性表示的表示法唯一.
定理3 如果向量组β1，β2，…，βt 可由向量组α1，α2，…，αs 线性表示，且t＞s，则β1，β2，…，βt 线性相关.（以少表多，多的相关）
【注】以t＝3，s＝2来证明，便于读者理解.
证 设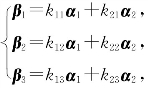
欲证β1，β2，β3 线性相关，只需证存在不全为零的数l1，l2，l3，使得
l1β1＋l2β2＋l3β3＝0，
即
l1（k11α1＋k21α2）＋l2（k12α1＋k22α2）＋l3（k13α1＋k23α2）＝0，
整理得(www.chuimin.cn)
（k11l1＋k12l2＋k13l3）α1＋（k21l1＋k22l2＋k23l3）α2＝0.
当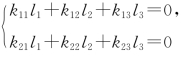
时，显然上式成立，而这个方程组是3个未知数l1，l2，l3，2个方程的情形，未知数个数大于方程个数，必有非零解l1，l2，l3，故β1，β2，β3 线性相关.
其等价命题：如果向量组β1，β2，…，βt 可由向量组α1，α2，…，αs 线性表示，且β1，β2，…，βt 线性无关，则t≤s.定理4 设m 个n 维向量α1，α2，…，αm，其中
则向量组α1，α2，…，αm 线性相关的充分必要条件是齐次线性方程组
有非零解，其中
【注】证 设
将②式左端写成矩阵形式，即得齐次线性方程组（Ⅰ）.因此，如果α1，α2，…，αm 线性相关，就必有不全为零的数x1，x2，…，xm 使①式成立，即齐次线性方程组（Ⅰ）有非零解；反之，如果齐次线性方程组（Ⅰ）有非零解，也就是有不全为零的数x1，x2，…，xm 使①式成立，则α1，α2，…，αm 线性相关.定理得证.
其等价命题：α1，α2，…，αm 线性无关的充分必要条件是齐次线性方程组（Ⅰ）只有零解.
【注1】如果n＜m，即方程个数小于未知数个数，齐次线性方程组（Ⅰ）求解时必有自由未知量，即必有非零解.因此，任何n＋1个n维向量都是线性相关的.所以在n维空间中，任何一个线性无关的向量组最多只能含n个向量.
【注2】n个n 维列向量α1，α2，…，αn 线性相关
有非零解.（线性无关
仅有零解）
仿定理4的研究方法，便有下面所给的定理5.
定理5 向量β可由向量组α1，α2，…，αs 线性表出
⇔非齐次线性方程组
＝x1α1＋x2α2＋…＋xsαs＝β有解
⇔r（α1，α2，…，αs）＝r（α1，α2，…，αs，β）.
（不能线性表出⇔Ax＝β无解⇔r（A）≠r（［A，β］））
定理6 如果向量组α1，α2，…，αm 中有一部分向量组线性相关，则整个向量组也线性相关.
【注】证 不妨设α1，α2，…，αj（j＜m）线性相关，于是有不全为零的数k1，k2，…，kj，使
k1α1＋k2α2＋…＋kjαj＝0.
从而有不全为零的数k1，k2，…，kj，0，…，0，使
k1α1＋k2α2＋…＋kjαj＋0αj＋1＋…＋0αm＝0，
故α1，α2，…，αm 也线性相关.
其逆否命题：如果α1，α2，…，αm 线性无关，则其任一部分向量组也线性无关.
总之，向量组部分线性相关，则整体也线性相关；整体线性无关，则任一部分也线性无关.
定理7 如果一组n维向量α1，α2，…，αs 线性无关，那么把这些向量对应相同位置各任意添加m 个分量所得到的新向量（n＋m 维）组α1*，α2*，…，αs*也是线性无关的；如果α1，α2，…，αs 线性相关，那么它们各去掉相同位置的若干个分量所得到的新向量组也是线性相关的.
【注】事实上，对于
Α＝［α1，α2，…，αs］，Β＝［α*1，α*2，…，α*s］，
其中α1*，α2*，…，αs*是分别在α1，α2，…，αs 对应相同位置各任意添加m 个分量.如果α1，α2，…，αs线性无关，即齐次线性方程组Ax＝0只有零解，则Bx＝0显然也只有零解（即α1*，α2*，…，αs*也线性无关）；反之，如果α1*，α2*，…，αs*线性相关，即Bx＝0有非零解，则Ax＝0也有非零解（即α1，α2，…，αs 也线性相关）.
有关张宇线性代数9讲的文章
- 详细阅读
-
张宇线性代数9讲：求解A矩阵详细阅读
，αm，βT线性无关.例5.16 已知齐次线性方程组A2×4x＝0的基础解系为ξ1＝［1，－1，3，2］T，ξ2＝［2，1，1，－3］T，则A＝________.应填，其中k1，l1，k2，l2 是不全为零的常数，且k1l2≠k2l1.由题设条件知，Aξ1＝0，Aξ2＝0，即两边转置，得作齐次线性方程组对系数矩阵作初等行变换，有取y2＝0，y3＝k，得，则解向量为取y2＝l，y3＝0，得，则解向量为其中k1，l1，k2，l2 是不全为零的常数，且k1l2≠k2l1.......
2023-11-21
- 详细阅读
-
秩的公式见第4讲-张宇线性代数9讲详细阅读
，tn－11］，α2＝［1，t2，…，tn－1r］，其中t1，t2，…＋kr，k1t1＋k2t2＋…，tr－1r］.由上述①的证明知β1，β2，…，tn－1r］，分别是向量β1，β2，…，1，－1］T，其中k是任意常数.......
2023-11-21
-
初等矩阵定义及特点-张宇线性代数9讲详细阅读
（1）定义（Eij，Eij（k），Ei（k））.①初等变换.（ⅰ）一个非零常数乘矩阵的某一行（列）.（ⅱ）互换矩阵中某两行（列）的位置.（ⅲ）将矩阵的某一行（列）的k倍加到另一行（列）.以上三种变换称为矩阵的初等行（列）变换，且分别称为倍乘、互换、倍加初等行（列）变换.②初等矩阵.由单位矩阵经过一次初等变换得到的矩阵称为初等矩阵.以3阶矩阵为例，并随之给出定义.（ⅰ）E2（k）＝，E 的第2行（或......
2023-11-21
- 详细阅读
-
《张宇线性代数9讲》首发十年，成为畅销书详细阅读
以《张宇高等数学18讲》为代表的考研数学36讲（包括《张宇高等数学18讲》《张宇线性代数9讲》《张宇概率论与数理统计9讲》（以下简称《36讲》））正式出版已有十年了.人们说，十年磨一剑，这第十版，理应在这套书的发展历程中具有里程碑式的意义.十年间，《36讲》从汇总课堂讲义出版时的名不见经传，到现在成为广大考研考生错爱的畅销书.在感谢读者厚爱和支持的同时，我深感责任重大、战战兢兢、如履薄冰，总是在思......
2023-11-21
-
张宇线性代数9讲中的三考法：解析，矩阵乘法规详细阅读
，0］，则Aβi＝0（i＝1，2，…，s）是Ax＝0的解.设矩阵Am×n，Bn×s，若AB＝C，则C是m×s矩阵.将B，C按行分块，有则γi＝ai1β1＋ai2β2＋…，m），故C的行向量是B 的行向量的线性组合.类似地，若A，C按列分块，则有则ξi＝α1b1i＋α2b2i＋…......
2023-11-21
相关推荐