微分中值定理在武汉东湖学院论文集中的教学探索

2023-12-04 理论教育版权反馈

【摘要】：二、微分中值定理之间的关系通过以上分析证明，引导学生归纳总结得出三个微分中值定理之间有如下关系：Rolle中值定理 Lagrange中值定理 Cauchy中值定理。

微分中值定理的教学探索

武汉东湖学院基础课部高等数学教研室　彭雪梅

众所周知，微分中值定理包括Rolle中值定理、Lagrange中值定理、Cauchy中值定理，它是微分学中的重要定理，在微积分学的理论及应用上都占有极其重要的地位，是教学内容的重点与难点。本文对这部分内容进行研讨，提出了在教学中的一些做法，这不仅有利于后续课程的学习，并且对学生掌握数学方法，运用数学方法解决实际问题将也是大有裨益的。

在微分中值定理的教学中，Rolle中值定理的证明借助于已经学过的最大值最小值存在定理、导数定义、极限性质等，证明过程比较直观，学生很容易接受。但在利用Rolle中值定理证明Lagrange中值定理和Cauchy中值定理时，若简单地按照教材的编排体系讲授，学生对辅助函数F(χ)的引入会产生“突然”和“神秘”的感觉，而且完成定理证明之后，学生对三个中值定理之间的联系难以把握，觉得内容太多不便记忆。所以，要达到让学生感到证明过程来得“自然”，消除“神秘”感，主动发现问题和解决问题，关键是通过启发引导，让学生通过思维、推理，自己发现符合条件的辅助函数，把辅助函数构造出来，并通过证明之后的归纳、反思，理清三个中值定理之间的联系以及各个定理的条件和结论的关系，准确地、深层次地掌握和应用定理。

一、微分中值定理的证明

Rolle中值定理的证明比较直观，学生很容易接受。下面主要讨论Lagrange中值定理和Cauchy中值定理的证明。

（一）用“分析法”证明Lagrange中值定理

Lagrange中值定理：如果函数f(x)满足

（1）在闭区间[a，b]上连续；

（2）在开区间(a,b)内可导，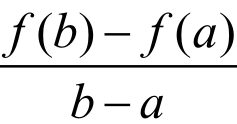

则至少存在一点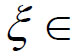(a,b)，使得f^'(x)=。

(若函数f(x)除了满足上面两个条件之外，还满足 ③ f(a)=f(b)

则至少存在一点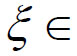(a,b)，使得f^'(x)=0。——这便是Rolle中值定理。）

1.提出问题，引导学生参与教学过程

在定理中要证明在(a,b)内至少存在一点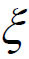，使得f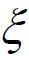^'()=，亦即

如果我们把上式左边看成是某个函数F(x)的导数在点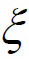的值，则问题变成需要构造一个辅助函数F(x)，使得F^'(x)=f^'(x)-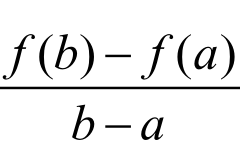，并且F(x)满足Rolle中值定理的条件，则根据Rolle中值定理，必存在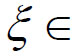(a,b)使得F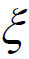^'()=0，亦即（**）式成立，则定理得证。

2.启迪学生思维，找出辅助函数

要使F^'(x)=f^'(x)-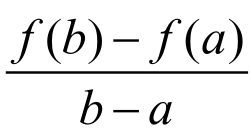，这样的F(x)应该如何构造呢？由于学生已经熟练地掌握了导数的运算，很快就能回答：

取F(x)=f(x)-。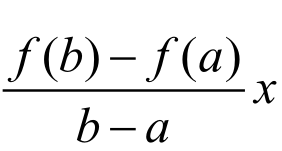

3.验证F(x)是否满足Rolle中值定理的条件

由于f(x)和y=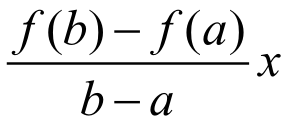都在[a，b]上连续，在(a,b)内可导，则

F(x)=f(x)-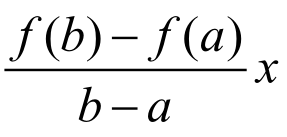也在[a，b]上连续，在(a,b)内可导，且F(b)=f(b)-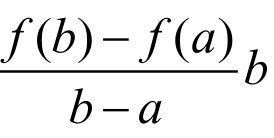，F(a)=f(a)-，则F(b)-F(a)=0，即F(b)=F(a)。

所以F(x)在[a，b]上满足Rolle中值定理的条件，根据Rolle中值定理，在(a,b)内至少存在一点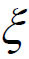，使得F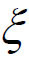^'()=0，即f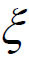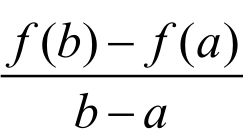^'()=，定理得证。

4.要求学生用“综合法”自己写出Lagrange中值定理的证明过程（略）。

（二）用类似的方法证明Cauchy中值定理：

Cauchy中值定理：如果函数f(x)，g(x)满足

（1）在闭区间[a，b]上连续；

（2）在开区间(a,b)内可导；

（3）在(a,b)内每一点都有g^'(x)≠0，

则至少存在一点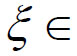(a,b)，使得=。

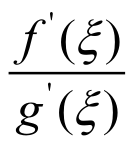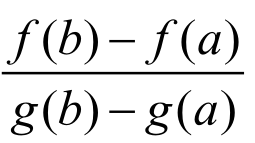类似证明Lagrange中值定理那样，进行如下几点。

1.提出问题，引导学生参与教学过程

将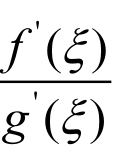=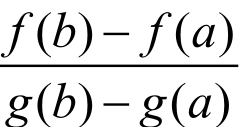经过适当变形，变成

如果我们把上式左边看成是某个函数F(x)的导数在点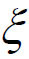的值，则问题变成需要构造一个辅助函数F(x)，使得F^'(x)=f^'(x)-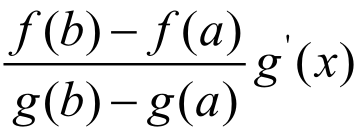，并且F(x)满足Rolle中值定理的条件，从而必存在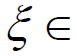(a,b)使得F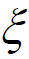^'()=0，亦即（***）式成立，则定理得证。(www.chuimin.cn)

2.找出辅助函数

怎样构造辅助函数F(x)呢？在Lagrange中值定理证明的基础上，学生

很快就能构造出F(x)=f(x)-。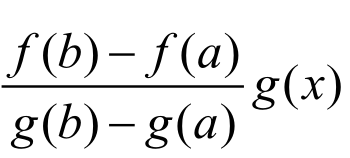

3.验证F(x)是否满足Rolle中值定理的条件

由于f(x)和g(x)都在[a，b]上连续，在(a,b)内可导，则

F(x)=f(x)-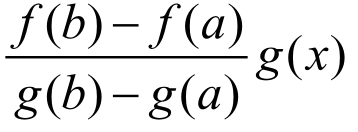也在[a，b]上连续，在(a,b)内可导，且F(b)-F(a)=0，即F(b)=F(a)。辅助函数F(x)在[a，b]上满足Rolle中值定理的条件，故在(a,b)内至少存在一点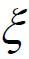，使得F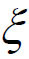^'()=0，即f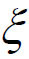^'()-=0，定理得证。

4.要求学生用“综合法”自己写出Cauchy中值定理的证明过程（略）。

二、微分中值定理之间的关系

通过以上分析证明，引导学生归纳总结得出三个微分中值定理之间有如下关系：

Rolle中值定理 Lagrange中值定理 Cauchy中值定理。

三、微分中值定理证明后的反思

为了进一步加深学生对三个定理的理解，准确把握定理的条件和结论之间的关系，我们可以提出以下几个问题让学生反思。

（一）辅助函数F(x)的构造是否是唯一的

结论：不唯一。在Lagrange中值定理的证明中还可取

F(x)=f(x)-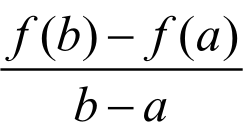(x-a)，或

F(x)=f(x)-f(a)-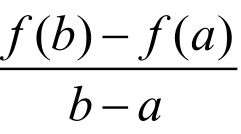(x-a);

在Cauchy中值定理的证明中还可取F(x)=f(x)-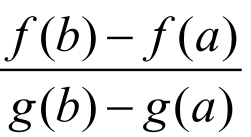g(x)+c（其中cR）。

可以验证这些函数仍然满足Rolle中值定理的条件，则必存在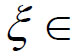(a,b)使得F^'(x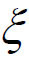)=0，从而定理得证。

（二）定理中的条件能否削弱或减少

结论：不能削弱也不能减少。以Lagrange 中值定理为例，如：函数f(x)=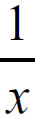，考虑区间[0，1]，函数在开区间(0,1)内可导，但在x=0处不连续，可以验证Lagrange中值定理的结论不成立（即条件不能削弱）。又如：函数f(x) =|x|，-1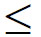x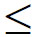1在闭区间[-1，1]上连续，但在开区间(-1,1)内不可导（因为在x = 0处不可导），可以验证Lagrange中值定理的结论不成立（即条件不能减少）。

事实上，三个中值定理的条件都不能削弱，而且三个中值定理中的条件都是缺一不可的，同学们可以举出反例，予以验证。

（三）定理中的条件是充分条件、必要条件、还是充要条件

结论：充分但不必要。以Lagrange中值定理为例，如：函数f(x)=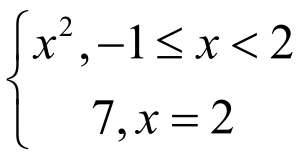

在开区间(-1,2)内可导且f^'(x)=2x，又f^'(1)==2，即存在

1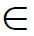(-1,2)使结论成立，但显然f(x)在区间[－1，2]上并不连续。该例表明定理的条件是充分条件而非必要条件。

四、回顾、总结与深入

微分中值定理是微分学的精华部分，是教学中的重点与难点，需要多次反复讨论才能使学生领会。在讲完这三个中值定理后（一般要两到三次才能讲完）需要回顾与总结，使学生能更深入地理解这些定理的实质。可向学生说明，这些定理之所以称之为中值定理，是指在一定条件下，函数值的增量（指区间端点处函数值之差）与区间内某些点的导数值存在密切的联系，即存在符合要求的中间值“x”。至于存在多少这种“中间值”以及这些“中间值”在区间内的分布情况，定理都没有进行讨论，但这并不妨碍这些定理的重要意义。它反映了可微函数的基本特征，给出了可微函数与其导数之间的关系.导数的主要应用正是通过这些中值定理体现的。此外，可比较用微分近似函数增量与有限增量公式之间的差异，这样便于将前面所学的知识与现在所学的知识内容联系起来，从而了解数学概念、理论的步步深入.

通过以上教学，学生对三个微分中值定理有了比较深入的理解，分析问题、解决问题及逻辑推理的能力得到了锻炼和提高。

【参考文献】

[1]吴波.浅谈高等数学课中微分中值定理教学法——反例教学法[J].思茅师范高等专科学校学报，2002（18）.

[2]王硕.关于微分中值定理教学的一点改革[J].工科数学，1998（14）.

[3]杨冰，钱淑英.微分中值定理的教学设计与实践[J].晋东南师范专科学校学报，2002（2）.

微分中值定理在武汉东湖学院论文集中的教学探索

相关推荐