力偶不同于力，它具有一些特殊的性质，现分述如下：力偶没有合力，不能用一个力来代替。这说明力偶对其作用面内任一点的矩恒等于力偶矩，而与矩心的位置无关。同一平面内的两个力偶，如果它们的力偶矩大小相等、转向相同，则这两个力偶等效，称为力偶的等效性。图3-10力偶的两个推论由以上分析可知，力偶对物体的转动效应完全取决于力偶矩的大小、力偶的转向及力偶作用面，即力偶的三要素。......
2025-09-29
平行四边形的基本性质：探索图形特征
【摘要】：欧几里得虽未给出一般平行四边形的定义,但在《几何原本》第一卷的第22 个定义中,给出了正方形、长方形、菱形、斜方形等特殊平行四边形的定义。关于平行四边形的性质,欧几里得在第一卷给出。此命题为平行四边形的性质定理。对角线二等分平行四边形图形可利用全等三角形证得,该性质也说明了平行四边形是中心对称图形。命题36 等底且在相同两平行线之间的平行四边形面积相等。
欧几里得虽未给出一般平行四边形的定义,但在《几何原本》第一卷的第22 个定义中,给出了正方形、长方形、菱形、斜方形等特殊平行四边形的定义。
在四边形中,四边相等且四个角是直角者称为正方形;角是直角,但四边不全相等者称为长方形;四边相等,但角不是直角者称为菱形;对角相等且对边亦相等,但边不全等且角不是直角者称为斜方形;其余四边形均为不规则四边形。
关于平行四边形的性质,欧几里得在第一卷给出。
命题33 在同一方向(分别)连接相等且平行的线段(端点),则连接线段相等且平行。
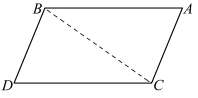
3.12.1 《几何原本》卷一命题33
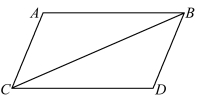
3.12.2 《几何原本》卷一命题34
添加辅助线BC,则根据平行线性质定理和三角形全等判定定理,容易得出结论。 此命题给出了平行四边形的判定方法之一:对边平行且相等。
命题34 在平行四边形中,对边相等,对角相等且对角线二等分其图形。(https://www.chuimin.cn)
此命题为平行四边形的性质定理。 对角线二等分平行四边形图形可利用全等三角形证得,该性质也说明了平行四边形是中心对称图形。
命题35 同底且在相同两平行线之间的平行四边形面积相等。
命题36 等底且在相同两平行线之间的平行四边形面积相等。
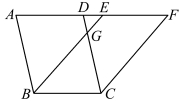
图3.12.3 《几何原本》卷一命题35
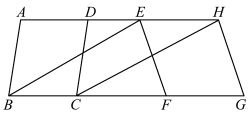
图3.12.4 《几何原本》卷一命题36
命题35 和命题36 是一对姊妹命题,两个命题的差别仅仅是一个字:“同”还是“等”。 依据命题35,容易推出命题36。
相关文章
- 详细阅读
-
建筑形态构成：性质与视觉特征详细阅读
图1-13点的形态点除了表示位置外，还可表示大小，它的大小是与其放置的环境对比而言的。点是力的中心，具有构成重点的作用，显现出视觉的中心，有时会起到定位和平衡的作用。......
2025-09-30
-
探索光致发光谱的性质与应用详细阅读
图2.5.1半导体中各种复合跃迁过程示意图[1]2.光致发光谱测量装置光致发光谱的测量装置主要可以分为光源、光路和分光系统、样品室、探测和数据记录系统四个部分,如图2.5.2所示。样品的光致发光经过透镜被收集和聚焦到单色仪的入射狭缝上,通过单色仪进行分光。......
2025-09-29
-
水资源评价方法与性质特征详细阅读
由于水资源内涵和外延对其评价的重要意义，国内也有不少学者对此做过深入探讨，但目前仍未达成较为一致的共识。因此，概念上的分歧造成水资源评价口径缺乏内在的一致性和层次性，直接导致了水资源评价量的巨大差异。水资源作为自然资源的组成，也应具备以上“有效性”和“可用性”基本特征。但是水资源可再生性不是不可破坏的。......
2025-09-30
-
城市生态规划的基本特征详细阅读
生态思维的兴起有着深厚的认识论和社会基础。从人类与自然界的关系角度来考虑，生态思维表现出如下特征。生态思维的进化性是基于生态系统内的生物与环境因子的进化而产生的。......
2025-09-30
-
傅里叶光学原理：卷积的基本性质详细阅读
下面以一维函数卷积为例，讨论卷积的主要性质。并且利用这一性质，很容易证明，两个复函数的卷积可以化为几个实函数卷积的线性叠加，并且运算的结果仍是复函数。卷积平滑效应的程度，完全取决于参与卷积各函数的分布特性。......
2025-09-30
-
傅里叶变换的基本性质及应用详细阅读
这一节,我们将介绍傅氏变换的几个重要性质,为了叙述方便,假定以下需求傅氏变换的函数都满足傅氏积分定理中的条件.1.线性性质设F1(w)=F[f1(t)],F2(w)=F[f2(t)],α,β是常数,则由于傅氏变换,傅氏逆变换是由积分定义的,而积分具有线性性质,所以傅氏变换,傅氏逆变换也具有线性性质.2.位移性质设F[F(t)]=F(w),则这个性质也称为时移性,它表明时间函数f(t)沿t 轴向左或......
2025-09-30
-
水循环的基本特征分析详细阅读
水循环具有下列特征:全球多年平均总蒸发量和全球多年平均总降水量相等。全球总水量为13.86亿km3，而参加水循环的水量只有52.0万km3，参加水循环的水量占全球水量的0.04%，若循环水量略增加一小部分，将使全球水资源利用量大为改观。海陆之间水交换的有效水量只占水循环量的极小部分。海洋输送到陆地上空的水汽只占海洋总蒸发量的8%，而92%的水汽以降水形式落回海洋。不同水体的循环速度相差甚大。大气圈中有52.0万km3水参加全年水循环。......
2025-09-29
相关推荐