最后，是从因果思维转向相关思维。当全部数据都加入分析的时候，只要有一个反例，因果关系就不成立，因此在大数据时代，因果关系变得几乎不可能。大数据透露出来的信息，确实会得出颠覆性的结论，所以我们不能用因果关系去探求其中的关联，而应该用相关思维去利用大数据带来的结论与价值。......
2025-09-29
三角形的五心：古巴比伦人到欧几里得时代的研究
【摘要】：关于三角形“五心”的最早发现,可追溯到古巴比伦人,其时间大约在公元前1700 年。基于生产实践经验,古巴比伦人已会求给定等腰三角形的外接圆半径等。可以推测,泰勒斯、毕达哥拉斯等数学家应对三角形的“五心”有所研究和发现,故至欧几里得时代“五心”均已被发现和研究。命题2 在已知圆内作一个与已知三角形等角的内接三角形。
关于三角形“五心”的最早发现,可追溯到古巴比伦人,其时间大约在公元前1700 年。 基于生产实践经验,古巴比伦人已会求给定等腰三角形的外接圆半径等。 其佐证是在现代伊朗发现的古巴比伦人泥板上记载:假设等腰三角形的高为40,底为60,则三角形的外接圆半径为31.25。
可以推测,泰勒斯、毕达哥拉斯等数学家应对三角形的“五心”有所研究和发现,故至欧几里得时代“五心”均已被发现和研究。 可能欧几里得认为,只有最重要的定理方能入选其著作,因而未把垂心定理和旁心定理收集到《几何原本》中。
在《几何原本》第四卷中,欧几里得首先给出“内接于圆”“外切于圆”“圆内切于图形”和“圆外切于图形”等定义,设有四个命题讨论了圆与三角形的关系。
命题2 在已知圆内作一个与已知三角形等角的内接三角形。
命题3 在已知圆外作一个与已知三角形等角的外切三角形。
命题4 求作已知三角形的内切圆。
命题5 求作已知三角形的外接圆。
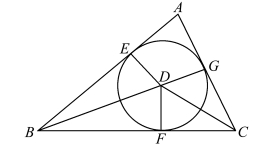
图3.11.5 《几何原本》第4 卷命题4(https://www.chuimin.cn)
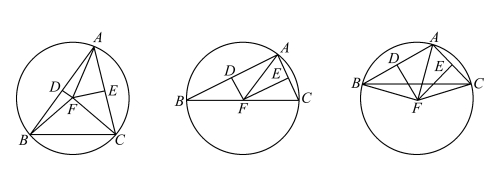
图3.11.6 《几何原本》第4 卷命题5
在命题5 中,欧几里得分3 种情形进行了讨论,其中第二种情形就是泰勒斯定理的推广。
阿基米德对三角形的重心进行了研究,并把结论推广到弓形、抛物线形等其它复杂图形。
三角形的外心、重心和垂心如此重要,你一定会想到它们之间有着某种联系。 1765 年,“数学家之英雄”欧拉在《三角形的几何学》中,发现和证明了欧拉线,即有欧拉定理:三角形的外心、垂心和重心都在一条直线上,而且外心和重心的距离为垂心和重心距离的一半。
显然,在图3.11.7 的直角三角形中,垂心H 与点B 重合,外心O 则是斜边AC 的中点,此时欧拉线成为斜边的中线。
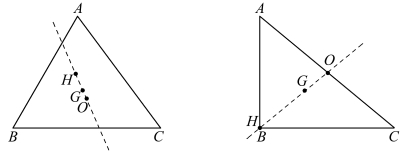
图3.11.7 欧拉线
相关文章
- 详细阅读
-
金融普惠到技术普惠：新时代的转变详细阅读
实际上，只有真正达到全链路金融科技技术服务，才能从各个方面解决金融普惠过程中的所有问题。最核心的要数市场风险，“度小满”为客户提供不同行业的区域监控，并针对金融普惠过程中常常出现的多头共债风险进行预警。纵观金融科技发展的这几年，金融普惠一直在推进，但技术普惠却不见进展。此所谓授人以鱼不如授人以渔，只有技术普惠，才能达成真正的金融普惠。......
2025-09-29
-
唐尧时代：五帝时期的后半段详细阅读
传说中的五帝时期可明显分为前后两大阶段，前半段是黄帝、少昊、颛顼、帝喾时期，从唐尧开始，进入后半段时期。虽然唐尧在五帝中排行在黄帝之后，但荣登正史的时间还早于黄帝，中国现存最早的史书《尚书》的叙述就是从唐尧开始。陶寺古城因被认为可能是帝尧时期的都城，而又被称为尧都。据《尚书·尧典》记载：“（唐尧）乃命羲和，钦若昊天，历象日月星辰，敬授人时。”......
2025-09-30
-
电影传统中的戏人电影：从费穆到张艺谋详细阅读
民间文化的消费者常常从一波三折的故事中获得娱悦、幻想与满足，因而电影容易与史传传统发生天然的黏合与亲近。“影戏”这个最具市民化的称谓，反映人们在对电影最基本的观念：电影如影戏一般，不过是个消遣、解闷的方式。电影面对传统文化的选择，必然与长于叙事，能从叙事中获得满足的史传文化传统发生较强的亲和力。其结果就是“戏人电影”[22]的出现。香港著名学者黄继持教授认为：“初期的电影却承受于传统艺术思想较多......
2025-09-29
-
人胸中各有个圣人，提高人的主体意识和自尊心详细阅读
在虔与于中、谦之同侍。于中起，不敢当。于中连忙站起来说道：“不敢当，不敢当。”“人胸中各有个圣人”的论断，是一种人性平等的思想，大大提高了人的主体意识和自尊心，更加坚定了人皆可以为圣贤的信心。......
2025-09-30
-
室町时代五山僧侣与文学详细阅读
和室町盛世时期相同，在室町末期，五山僧侣也得到了室町幕府的征夷大将军的礼遇，五山僧侣在政治上和学问上都有很大的势力。五山僧侣有很多宗派，其中禅宗势力最大。所幸的是，五山僧侣在地方上得到了保护，五山文学得以维持。五山僧侣逃到小仓之后，得到了资助，在这里讲学、研究学问。室町末期，五山僧侣中有名的有得岩、龙派、真玄、清播四家。灵彦终生不愿为官，颇受世人敬仰，位列五山长老之上。......
2025-09-29
-
从五县到九县：县市区的拓展详细阅读
民国二十九年7月，以南田县全部境域及宁海县东南部18乡镇、临海县东北部五乡镇置三门县，以地濒三门湾而得名。第二次是在1958年12月，撤销台州专区，天台县划属宁波专区，临海仙居黄岩温岭四县划属温州专区。并将临海县章安区、黄岩县洪家区、三甲区又划属椒江。至此台州市辖临海温岭两县级市，椒江黄岩路桥三区，玉环天台仙居三门四县，一共九个县（市、区）。因此海门归属黄岩管辖，总共才25年时间。......
2025-09-29
-
人要识心体，自然不得增减-传习录详细阅读
澄在鸿胪寺仓居①，忽家信至，言儿病危，澄心甚忧闷，不能堪。王阳明于正德九年升任南京鸿胪寺卿，许多弟子随他前往。仓居，在衙舍居住。②有所忧患不得其正：出自《大学》。出自《孝经·丧亲》。陆澄在南京鸿胪寺的衙门里居住的时候，突然接到儿子病危的家信，顿感忧郁，无法忍受。毁不灭性的功夫，王阳明说，需要“在此时磨炼”，能及时克制住大悲大喜。这就是王阳明的“天理本体，自有分限”，所以“不可过也”。......
2025-09-30
相关推荐