对于给定的数列｛xn｝，我们讨论当项数n无限增大时（记作n→∞），对应项的变化趋势.观察上面的四个数列，容易看出，当n→∞时，数列趋于1；数列各项的值在数1的两侧来回交替着变化，且越来越接近1；数列｛2n－1｝越来越大，无限增大；数列｛1－（－1）n｝各项的值永远在0与2之间交互取得，而不与某一数接近.如果当n→∞时，数列的项xn能无限接近于某个常数A，则称这个数列为收敛数列，常数A称为当n→∞时......
2025-09-30
自变量x趋无穷大时的函数极限：高等数学上册
【摘要】：观察函数当x趋近于∞时发现：当x趋近于∞时对应的函数值无限地与数值0接近，即当因此数值0为函数当x→∞时的极限.设a为某常数，如果当｜x｜无限增大时，函数f（x）与a可无限地接近，则称a是函数f（x）当x→∞时的极限，记作或f（x）→a（当x→∞时）.式“x→∞”表示自变量x的绝对值无限增大的变化过程，在数轴上看，“x→∞”表示x沿着数轴向两边（或分别向右、左）移动，并离原点的距离越来越远，直至无
观察函数
当x趋近于∞时发现：当x趋近于∞时
对应的函数值无限地与数值0接近，即当
因此数值0为函数
当x→∞时的极限.
设a为某常数，如果当｜x｜无限增大时，函数f（x）与a可无限地接近，则称a是函数f（x）当x→∞时的极限，记作
或f（x）→a（当x→∞时）.
式“x→∞”表示自变量x的绝对值无限增大的变化过程，在数轴上看，“x→∞”表示x沿着数轴向两边（或分别向右、左）移动，并离原点的距离越来越远，直至无限远，这种变化过程称为x趋于无穷大，记作x→∞.用｜x｜表示x与原点的距离，则x→∞就是｜x｜越来越大，若用X表示一个很大的正数，则不等式｜x｜＞X表示x是那些与原点的距离比X还远的点.
式“f（x）→a”表示函数f（x）与常数a可无限接近的变化趋势.如果任取小正数ε，则式｜f（x）－a｜＜ε就表示函数f（x）与a的距离之小，可以小于预先任意给定的小正数ε.
极限
表达了一个因果关系：若条件“x→∞”成立，就有结论“f（x）→a”成立.因此也可理解成：当x离原点的距离充分远，即｜x｜充分大时，函数f（x）与a可充分地接近；当x离原点的距离无限远，即｜x｜无限大时，则函数f（x）与a就无限地接近.
因此极限
的意思是：对于预先任意给定的小正数ε，式子｜f（x）－a｜＜ε成立的条件是｜x｜要充分大.这个“充分大”，我们用式子｜x｜＞X表示（这时｜x｜比X还大）.这里X表示足够大的正数，因此如果相应于前面给定的ε，存在一个足够大的数X，当满足条件｜x｜＞X时（x充分大时），对应的函数值就满足不等式｜f（x）－a｜＜ε（函数f（x）与a就充分地接近），由于ε可以无限小，函数f（x）与a就能无限地接近，因此就有极限
由此，我们得到自变量x无限增大时函数极限的精确定义.
定义1 设函数f（x）在｜x｜大于某一正数时有定义，a为某常数，如果对任意给定的小正数ε，总存在一个正数X，使得当｜x｜＞X时，不等式｜f（x）－a｜＜ε都成立，则称a是函数f（x）当x→∞时的极限，记作
（若定义1中的常数a不存在，就称极限
不存在，或称f（x）当x→∞时发散.）
定义1可用ε－X语言简单地表述为若∀ε＞0，∃X＞0，使得当｜x｜＞X时，恒有｜f（x）－a｜＜ε成立，则称函数f（x）当x→∞时的极限为a，记作
a.
从几何上看
的意义是：对于∀ε＞0，必∃X＞0，使得当x满足｜x｜＞X时，曲线y＝f（x）上对应的点一定落在两条直线y＝a＋ε和y＝a－ε之间（图1－19）.
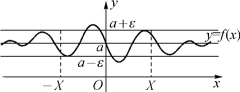
图1－19
例1 证明
证 ∀ε＞0，由不等式(https://www.chuimin.cn)
解得
因此只要取
即有
∀ε＞0，当｜x｜＞X时，不等式
恒成立.即
例2 证明
证 ∀ε＞0，由不等式
解得
因此只要取
即有
∀ε＞0，当｜x｜＞X时，不等式
恒成立.即
相关文章
- 详细阅读
-
高等数学学习指导：函数、极限与连续详细阅读
知识要点一、函数的概念1.函数、反函数、基本初等函数、初等函数、复合函数的定义.2.理解函数记号y=f（x）中“f”的意义.函数的两个要素，对于两个或两个以上的函数，只有定义域和对应法则完全相同时才是同一函数.3.弄清基本初等函数的概念，熟悉这些函数的特性.4.求f（x）的定义域.对于较复杂的函数求定义域问题，就是求解由简单函数的定义域所构成的不等式组的解集.5.函数的重要性质：有界性，奇偶性，周......
2025-09-30
-
函数极限与左、右极限关系详细阅读
【主要内容】1.设函数f（x）在点x0的某个去心邻域内有定义，则limx的充分必要条件是注 （ⅰ）对任意ε>0，如果存在δ>0，当0<|x-x0|<δ时有|f（x）-A|<ε.对任意ε>0，存在δ>0，使得-δ
2025-09-30
- 详细阅读
-
复变函数的极限与连续性详解详细阅读
复变函数和实变函数类似,同样可以讨论函数的极限和连续性,且形式基本上与实变函数一致.现在介绍复变函数的极限概念.定义3 设函数w = f(z)在点z0的去心邻域:0 ＜|z - z0| ＜ρ内有定义.如果存在一个复常数A,使得对于任意给定的ε ＞0,总存在一个实数δ ＞0(δ ＜ρ),当0 ＜|z-z0|＜δ 时,有|f(z)-A|＜ε,我们称A为f(z)当z趋于z0时的极限,记为复变函数极限的几......
2025-09-30
-
高等数学：函数基本性态详细阅读
初等数学中已经简单介绍了函数的有界性、单调性、奇偶性、周期性，下面分别对它们作简要概括.1）有界性定义3设函数f（x）在区间I上有定义，若存在数M1，使得当x∈I时，恒有f（x）≤M1则称函数f（x）在数集I上有上界，M1为f（x）在I上的一个上界；若存在数M2，使得当x∈I时，恒有f（x）≥M2则称函数f（x）在数集I上有下界，M2为f（x）在I上的一个下界；若f（x）在数集I上既有上界，又有......
2025-09-30
-
高等数学：二重极限定义及性质详细阅读
定义2 设二元函数点f（x，y）在点P0（x0，y0）的某邻域内有定义（点P0可以除外），如果该邻域内的点P（x，y）以任意方式无限趋于点P0（x0，y0）时，对应的函数值f（x，y）无限接近于一个确定的常数A，则称常数A为函数f（x，y）当（x，y）→（x0，y0）时的极限，记作为了区别于一元函数的极限，我们把二元函数的极限叫作二重极限.必须注意，所谓二重极限存在，是指点P（x，y）以任何方式趋......
2025-09-30
-
函数在无穷远点的留数的应用详细阅读
设函数f(z)在z = ∞的去心邻域R ＜|z| ＜+∞内解析,C 为该邻域内包含圆周|z| = R 的任一条简单闭曲线,则闭曲线C环绕z = ∞的正向,就是C环绕z =0的负向,因此我们可定义函数f(z) 在z =∞的留数为定义2 设z =∞是函数f(z)的孤立奇点,f(z)在z =∞心邻域R ＜|z|＜+∞内解析,f(z)在z =∞的留数其中C为包含圆周|z|=R只的任一条正向简单闭曲线.设函......
2025-09-30
相关推荐