桥梁不确定性分析与应用

2023-09-19 理论教育版权反馈

【摘要】：根据不确定性在短时间内变化与否，可将不确定性因素分为静态不确定性和动态不确定性。动态不确定性则受时间影响较大，且表现出明显的动力特征，例如风荷载、汽车荷载和地震荷载等。图1.1随机因素的三角关系模型我国学者赵国藩院士［5］将工程结构的不确定性分为事件的随机性、事物的模糊性、人类知识的不完善性三类。不确定性的处理方法方面，目前的研究成果主要集中于概率论、模糊数学、证据理论、灰色系统等方面［7］。

工程结构在设计、施工和使用过程中存在大量不确定性因素，例如荷载的随机性、结构抗力的模糊性以及信息的不完善性等，这些不确定性因素直接影响到结构的安全性、适用性和耐久性。工程结构可靠性是研究工程结构在各种不确定因素作用下的安全问题，其分析目的就是对结构安全的不确定性进行概率评估，以确保工程结构的安全水平。工程结构中的不确定性构成了工程结构可靠度研究的前提与重要内容［1］。工程结构的主要不确定性来源于工程结构本身、外部荷载作用以及计算分析方法的不确定性。工程中的不确定性有其自身特点，主要表现为结构参数的随机性、荷载作用的随机性、计算模型的不确定性等。其中，结构参数的随机性主要表现在结构材料特征、几何尺寸、边界条件和初始条件等方面［2］。荷载作用的随机性主要表现在风荷载、汽车荷载、地震荷载和温度荷载等方面。计算模型的不确定性主要是指失效模式的不确定性。

结构的不确定性具有时变特征，会随着社会的发展而变化。根据不确定性在短时间内变化与否，可将不确定性因素分为静态不确定性和动态不确定性。静态不确定性是指不确定性因素受时间的影响较小，例如结构的自重和预应力等。动态不确定性则受时间影响较大，且表现出明显的动力特征，例如风荷载、汽车荷载和地震荷载等。

根据不确定性因素产生的机理和物理意义的不同，工程结构的不确定性源可归为3类：随机性、模糊性和未知性。针对上述3类不确定性的描述方法，可采用3种不确定性模型描述：随机模型、模糊模型、凸集模型，如图1.1（a）所示。吕震宙等［3］基于上述模型建立带有重心的可靠性三角模型，如图1.1（b）所示。

从不确定性的来源方面来看，不确定性主要包括［4］：结构基本变量的不确定性，如材料性能参数和荷载作用等，这类不确定性可以直接测量；描述随机变量的模型的不确定性；推导待定值模型的不确定性，例如钢筋混凝土轴心受压构件正截面承载力公式；推断概率模型参数的不确定性；人为的主观因素的不确定性，例如结构设计、建造和维护过程中人们的决策错误等。

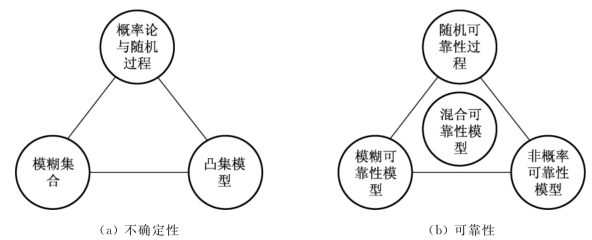
pagenumber_ebook=12,pagenumber_book=2

图1.1　随机因素的三角关系模型

我国学者赵国藩院士［5］将工程结构的不确定性分为事件的随机性、事物的模糊性、人类知识的不完善性三类。其中，随机性主要是指工程结构参数的不确定性、统计不确定性以及结构模型的不确定性；工程结构的模糊性主要指工程结构参数的不分明或过渡性的不确定性，即参数属于的某个集合的边界是不确定的，例如事物的好与坏，美丽与丑陋并无明确的标准；知识的不完善性主要是指人类对事物的主观认识的局限性，例如知道事物的变化趋势，但无法预测变化程序。

王光远院士［6］将工程结构的不确定性分为三类：未来事物的随机性、概念外延的模糊性、主观认识的不确定性。其中，未来事物的随机性主要是指一些偶然因素作用致使事件的结果不可准确地预知，包括条件的不确定性和因果关系的不明确性。虽然工程结构十分复杂，但其力学行为与荷载作用下的结构响应是有规律可循的。概念外延的模型性主要是指事物边界的模糊性，不可能给某些事物以明确的定义和评定标准而形成的不确定性，主要表现在某些论域的模糊集合。主观认识的不完备性除了某些概率外延的模糊性外的由于信息不完整而带来的不确定性外，主要是由于决策者的信息不完整而带来的主观上的不确定性。

不确定性的处理方法方面，目前的研究成果主要集中于概率论、模糊数学、证据理论、灰色系统等方面［7］。概率论主要研究事物的随机性，利用概率描述事物的变化。目前的公理化定义使得概率在数学上能够准确地描述各类复杂随机现象，事实上，结构可靠度理论也是基于概率论而迅速发展起来的。基于无信息先验分布的贝叶斯方法为不确定量化的发展提供了较好的方法基础［8］。在处理工程结构中的模糊性而发展起来的模糊数学理论在模式识别、聚类分析、综合评判和决策等方面得到了广泛的应用［9-10］。证据理论主要研究基于证据推理过程，处理认识和推理过程中的不确定现象。

桥梁不确定性分析与应用

相关推荐