流体速度与加速度的关系

2025-09-29 理论教育版权反馈

【摘要】：由于流体的速度与加速度是描述流体运动的两个主要运动参数，这里对它们做重点说明。流体加速度的计算公式代表的物理意义因而为“流体流动的加速度＝当地加速度＋对流加速度”。有人常误以为如果流体流动为稳态流动，则流体的加速度就一定为 0，这是一个错误的。假设空气的流动过程为稳态流动，且气流的流速可以表示为求空气气流的加速。

由于流体的速度与加速度是描述流体运动的两个主要运动参数，这里对它们做重点说明。

6.5.1 流体的速度

6.5.2 流体的加速度

所谓流体的加速度（Acceleration）用来描述流体的流动速度随着时间改变的程度。如果流体的流动速度随着时间的改变而改变，则此运动称为变速度运动（Variable velocity motion）。因为速度是一个向量，同时具有大小和方向，所以只要速度的大小或方向改变，都属于变速度。因为，因此其加速度要用到链式法则（Chain rule）。

1．计算公式的描述

2．计算公式的推导

流体的加速度采用链式法则推导过程描述如下。

3．计算公式代表的物理意义

流体加速度的计算通式为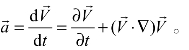 pagenumber_ebook=144,pagenumber_book=137 式中，项与位置无关，称为当地加速度（Local acceleration）；项则是流体流速随着流场位置的变化而产生，是由于流场的流速不均匀而产生的，所以称为对流加速度（Convective acceleration）。流体加速度的计算公式代表的物理意义因而为“流体流动的加速度＝当地加速度＋对流加速度”。有人常误以为如果流体流动为稳态流动，则流体的加速度就一定为 0，这是一个错误的。因为流体流动为稳态，流体的当地加速度为0，但是流体的对流加速度不一定为0，因此流体的加速度也不一定为0。