弹体头部形状变化对装药损伤断裂的影响

2025-09-29 理论教育版权反馈

【摘要】：弹头形状对弹体在侵彻过程中承受的过载有影响［10］。图5－31所示为装药损伤度α 随时间的变化情况。三种弹头形状装药的最终装药损伤度αm分别为4.68%、1.47%和0.11%。计算研究表明，弹头曲径比增加会使装药最大裂纹宽度减小，装药的装药损伤度也随之降低。图5－33 所示为不同弹头曲径比的缩比弹装药的最终装药损伤度αm的拟合曲线，随着Ψ 的增大，αm在AB 段呈现出下降趋势，在B 点达到极小值。

弹头形状对弹体在侵彻过程中承受的过载有影响［10］。保持装药结构和弹体质量不变，改变弹头曲径比Ψ，建立几组模型进行计算，研究弹头曲径比1 ＜Ψ ＜4 时装药的动态损伤。图5－26 所示分别为Ψ＝1，Ψ＝2.6，Ψ＝4 的1／4 缩比弹模型。

pagenumber_ebook=118,pagenumber_book=98

图5－26　弹头曲径比Ψ 分别为1、2.6 和4 的缩比弹模型

（a）Ψ＝1 的缩比弹；（b）Ψ＝2.6 的缩比弹；（c）Ψ＝4 的缩比弹

计算得到弹体和装药的过载曲线如图5－27 所示。当Ψ＝1 时，侵彻深度为38.0 cm，侵彻时间为1.42 ms，弹体最大过载为577 99g （g＝9.8 m／s2），装药最大过载为90 450 g；当Ψ＝2.6 时，侵彻深度为49.6 cm，侵彻时间为1.95 ms，弹体最大过载为48 553g，装药最大过载为62 571g；当Ψ＝4 时，侵彻深度为54.5 cm，侵彻时间为2.22 ms，弹体最大过载为43 945g，装药最大过载为55 960g。不同曲径比下装药的最大过载都要大于弹体的平均过载峰值，这是由于弹体和装药之间的相对运动导致的。随着弹头曲径比增大，侵彻深度和侵彻时间增大，而弹体和装药的过载减小。

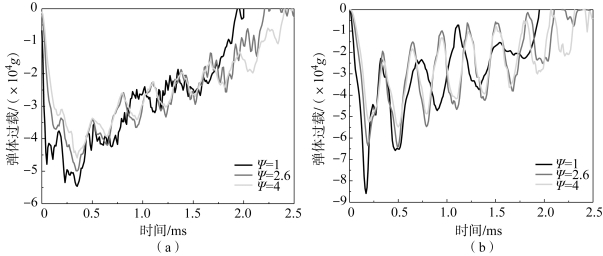
pagenumber_ebook=118,pagenumber_book=98

图5－27　不同着靶速度下弹体和装药过载随时间变化

（a）弹体；（b）装药过载

图5－28 所示为三种弹头形状的缩比弹侵彻结束时装药无量纲裂纹宽度ω的云图，表征了装药的损伤情况，图中单元的裂纹宽度有蓝色到红色逐渐增大。当Ψ＝1 时，裂纹在分布于装药各个部位，头部和尾部由于受到较大过载，受压产生严重损伤；中间部位受到拉应力和压应力的反复作用，裂纹横向扩展，形成断面。当Ψ＝2.6 时，装药头部和中部仍有明显裂纹，而尾部装药几乎没有损伤。当Ψ＝4 时，裂纹仅存在于头部和靠近尾部的位置，裂纹区域明显减少。

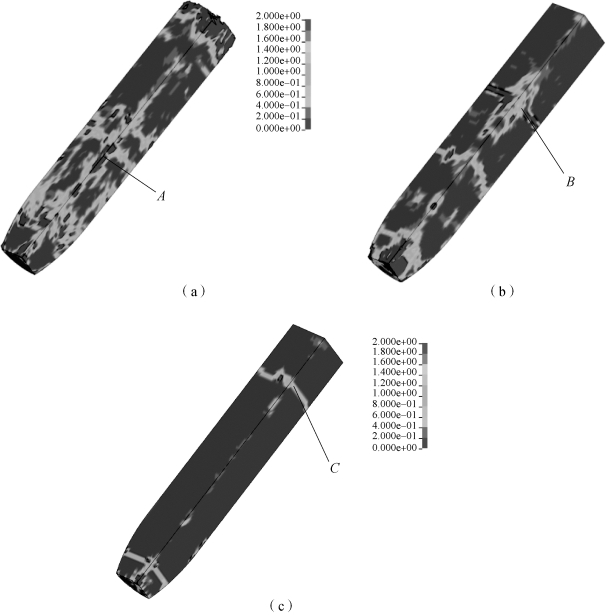
pagenumber_ebook=119,pagenumber_book=99

图5－28　装药的最终损伤示意图（见彩插）

（a）Ψ＝1；（b）Ψ＝2.6；（c）Ψ＝4

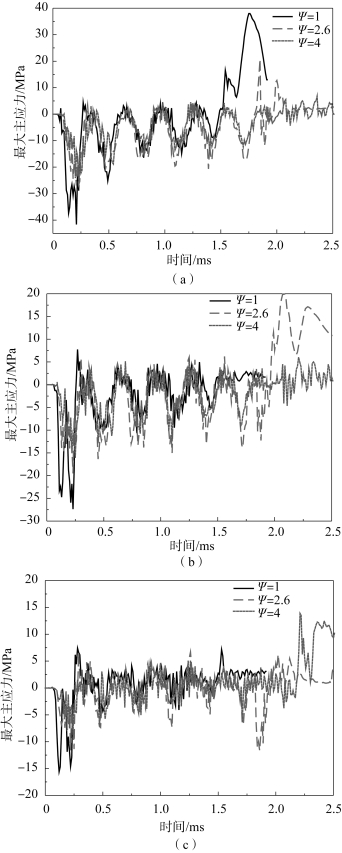
将图5－28 中箭头指向处A、B、C 的最大主应力与另外两个模型相应位置的最大主应力作比较。图5－29 （a）表示三种弹体装药在A 点的最大主应力，最大主应力在1.5 ms 之前没有太大差别，随后Ψ＝1 和Ψ＝2.6 的最大主应力值突然增大，对应图5－27 中A 点处Ψ＝1 和Ψ＝2.6 的装药都有裂纹存在。Ψ＝1 的最大主应力最大值比Ψ＝2.6 的最大主应力大，对应图5－28 中Ψ＝1 装药在A 点处的裂纹宽度大于Ψ＝2.6 装药的裂纹宽度。同样，在图5－29 （b）和（c）中也出现了与图5－29 （a）中相同的现象。由图可以看出，单元最大主应力的突然增大导致单元裂纹宽度急剧增大，从而形成裂纹。

pagenumber_ebook=120,pagenumber_book=100 (https://www.chuimin.cn)

图5－29　装药指定位置的最大主应力随时间的变化

（a）A 点；（b）B 点；（c）C 点

图5－30 所示为单元最大裂纹宽度随时间的变化。在0.4 ms 之前，三种曲径比下的装药最大裂纹宽度增长趋势相似。随后，Ψ＝1 和Ψ＝2.6 装药的单元最大裂纹宽度急剧增加，在0.6 ms 时Ψ＝1 装药的单元最大裂纹宽度超过1.1 mm，在1.25 ms 时Ψ＝2.6 装药的单元最大裂纹宽度超过1.1 mm。而Ψ＝4 装药的裂纹宽度增长缓慢，最终最大裂纹宽度仅为0.62 mm。由于材料模型设置了单元删除阈值，当单元裂纹宽度超过1.1 mm 时，该单元将会被删除，因此侵彻结束后Ψ＝1 和Ψ＝2.6 的装药最大裂纹宽度都超过了1.1 mm。

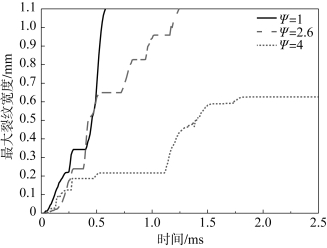
pagenumber_ebook=121,pagenumber_book=101

图5－30　单元最大裂纹宽度随时间的变化

将宽度超过0.1 mm 的裂纹定义为可见裂纹，用α 表示裂纹宽度超过0.1 mm 的单元占装药的体积比，即可见裂纹含量（装药损伤度）。图5－31所示为装药损伤度α 随时间的变化情况。在侵彻过程中，Ψ＝1 的装药可见裂纹持续增长；Ψ＝2.6 装药的可见裂纹在2 ms 之前增长缓慢，随后快速增长；Ψ＝4 装药的可见裂纹增长速度最慢。三种弹头形状装药的最终装药损伤度αm分别为4.68%、1.47%和0.11%。计算研究表明，弹头曲径比增加会使装药最大裂纹宽度减小，装药的装药损伤度也随之降低。

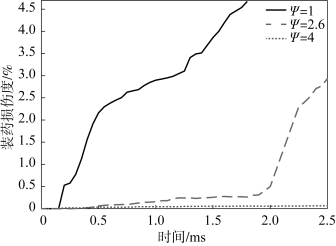
pagenumber_ebook=121,pagenumber_book=101

图5－31　装药损伤度α 随时间的变化情况

对弹头曲径比1 ＜Ψ ＜4 的几组缩比弹模型进行计算，得到装药过载和装药损伤等结果。对不同弹头曲径比的缩比弹在侵彻过程中装药的最大过载进行拟合，如图5－32 所示。由图可以看出，虽然装药最大过载要大于弹头最大过载，但是其随曲径比的变化趋势与弹头最大过载相似，当Ψ ＞3.5 时装药最大过载值减小变缓。图5－33 所示为不同弹头曲径比的缩比弹装药的最终装药损伤度αm的拟合曲线，随着Ψ 的增大，αm在AB 段呈现出下降趋势，在B 点达到极小值。随后，αm在BC 段增加，αm在C 点的值小于在A 点的值。αm在CD 段又出现下降的趋势，αm在D 点之后减小十分缓慢。因此使Ψ ＞3.5 能够有效地减小弹体内部装药的最大过载和最终可见裂纹含量，尖卵形弹头曲径比取3.5 ＜Ψ ＜4 能够有效保护弹体内部装药。

pagenumber_ebook=122,pagenumber_book=102

图5－32　装药最大过载与曲径比Ψ 的关系

pagenumber_ebook=122,pagenumber_book=102

图5－33　装药最终装药损伤度与曲径比Ψ 的关系

弹体头部形状变化对装药损伤断裂的影响

相关推荐