实际应用中经常遇到这样的拉普拉斯方程的边值问题一广义狄利克莱(Dirichlet) 问题.即设Γ是有限复平面上单连通域D的边界,又定义函数g(p)在Γ上连续,或至多有有限个第一类间断点.试求在D内有界的调和函数φ(x,y),使对g(p)在Γ上的连续点P满足这类问题中,对于区域D比较简单的情形,有时可直接利用在D内解析函数的实部或虚部都是调和函数来直接得到所求问题的解.但当区域复杂时,我们可通过一个......
2023-10-30
推导拉普拉斯方程
【摘要】：由于液体具有表面张力，液面往往显示不同程度的弯曲，弯曲液面的一个根本特性就是曲面两侧存在压力差。相应地AB边长由x变为x+dx，BC边长由y变为y+dy，AA′的距离为dz，于是面积增量为dA=-xy=xdy+ydx 体积增量为dV=xydz 式变为由相似三角形的比较可知：代入式可得若液面为球形，R1=R2=R，式变为图3-1-4任意曲面元的扩大示意图式就是著名的拉普拉斯方程。
由于液体具有表面张力，液面往往显示不同程度的弯曲，弯曲液面的一个根本特性就是曲面两侧存在压力差。例如，用一根小管吹肥皂泡后，必须把管的另一端堵住，泡才能存在，否则就自行收缩了。这就是因为弯曲液面两侧有压力差。此压力差与体系的关系可推导如下：
设容积一定的箱中有一液滴，箱中大气压力为p，液滴内部压力为p′=p+Δp，根据平衡条件，在恒温时，
dG=-p′dVl-pdVg+σdA=0 （3-1-7）
其中，下标l和g分别表示液体和气体。因为体系总体积恒定，dVl=-dVg，可得
（p-p′）dVl+σdA=0 （3-1-8）
于是：
考虑任意曲面上的一个小面积元ABCD，其主半径为R1及R2（图3-1-4）。体积扩大dV时，液面扩大dA，面积元变为A′B′C′D′。相应地AB边长由x变为x+dx，BC边长由y变为y+dy，AA′的距离为dz，于是面积增量为
dA=（x+dx）（y+dy）-xy=xdy+ydx （3-1-10）
体积增量（曲面移动扫过的体积）为
dV=xydz （3-1-11）
式（3-1-9）变为
由相似三角形的比较可知：
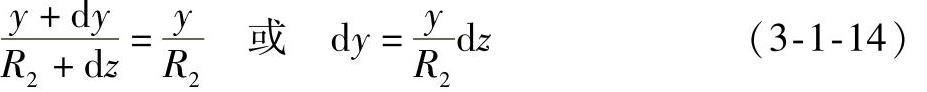
代入式（3-1-12）可得
若液面为球形，R1=R2=R，式（3-1-15）变为
图3-1-4任意曲面元的扩大示意图
式（3-1-15）就是著名的拉普拉斯方程。一般情况下，凸液面的液相压力大于气相，Δp＞0，R取正值；凹液面的液相压力小于气相，Δp＜0，R取负值；若为平液面时，则两相压力相等，Δp=0，R→∞。
有关焊接方法与过程控制基础的文章
- 详细阅读
-
推导推移质公式详细阅读
推移质公式推求当运动泥沙与床面泥沙的交换达到平衡，即单位时间内自单位床面上冲刷外移的泥沙数量正好与沉积下来的泥沙数量保持相等时的输沙率。Einstein 经过推导得出在单位面积上将有重量为的泥沙被冲刷外移，其中A1、A2为与泥沙颗粒形状有关的系数。图1-2修正的Einstein公式与实测资料的对比图1-2修正的Einstein公式与实测资料的对比......
2023-06-22
-
角度变换公式推导详解详细阅读
图6.10坐标系旋转如图6.10所示，假定在车体处于初始水平位置时，火炮的指向为此时炮塔系统的方位角为φ，俯仰角为θ。图6.10坐标系旋转上述坐标旋转的顺序不唯一，α、β以及γ排列的六种旋转次序都会使火炮的最终指向为。令则可以得到的表达式同时，角∠Z0Z2P0的表达式为在球面三角Z0P0Z2中，已知。下一节将在这一前提下，建立无人炮塔的动力学模型。......
2023-06-24
- 详细阅读
-
PCA的理论原理和推导过程详细阅读
图10－1PCA推导在图10－1中，u1就是主成分方向，然后在二维空间中取与u1方向正交的方向，就是u2的方向。则n个数据在u1轴的离散程度最大，即方差最大，数据在u1上的投影代表了原始数据的绝大部分信息，即使不考虑u2，信息损失也不多。PCA有两种通俗易懂的解释:①最大方差理论；②最小化降维造成的损失。如图10－1所示，样本在u1上的投影方差较大，在u2上的投影方差较小，那么可认为u2上的投影是由噪声引起的。......
2023-06-21
-
单相流的连续方程求解详细阅读
在流场中任取一个控制体Ω，该控制体内有多孔固体介质，孔隙度为φ。多孔介质被流体所饱和。在控制体内任意取一体元dΩ进行研究。在多孔介质不变形的情况下，孔隙度φ保持恒定，则φ可从偏导数中分离出来。式是非稳态有源流动连续性方程的一般形式。根据三维达西流方程，有当域内不存在源或汇时，非稳态渗流的连续性方程转化为对于流体不可压缩情形，连续性方程转化为......
2023-06-28
-
颗粒流基本方程简介详细阅读
将φ 乘以Boltzmann方程的两边，对整个颗粒脉动速度空间积分，获得φ 的输运方程。因此，可以通过假设颗粒的速度分布函数获得颗粒流的应力和能量通量等的表达式，或者用统计平均的办法建立各类守恒型方程来描述颗粒流的平均运动。因此，需要通过一定假设，建立泥沙颗粒相的本构关系。......
2023-06-22
- 详细阅读
相关推荐