式中的系数Z11、Z12、Z21、Z22具有阻抗性质，所以式称为阻抗方程或Z方程。由此得出即Z12是输入端口开路时的转移阻抗，称为开路转移阻抗。无源线性二端口网络如果同时满足式 时，则Z参数中只有两个参数是独立的。......
2023-06-24
地表水量平衡方程参数率定方法简介
【摘要】：对于地表汇流过程，有地表水量平衡方程进而，可采用最小二乘法估计出参数g3。传统的率定瞬时单位线的方法，是假定流域降雨径流系统为线性时不变系统的前提下，采用统计数学中的矩法来计算参数（n，K）。传统的率定线性水库参数的方法，是从实测流量过程线中根据组合退水曲线识别洪水过程的退水段，确定退水曲线Qt=Q0·e-t/K的起始点。选择多组退水过程观测值，利用最小二乘法可估计消退系数。
1.产流模型参数识别
时变增益的TVGM产流模型参数为（g1，g2，g3）。
产流参数识别的原理是基于产汇流的水量平衡方程
式中 Q——流量，m3/s；
R——净雨量，mm；
T——一个足够长的时段。
事实上，流量序列可视为净雨的时间分配过程，对于一个足够长的时段，可以保证式（3-1-26）水量平衡方程式的成立。
取定一个影响长度Tm（通常取系统记忆长度的某个倍数）后，对于不同的产流过程，均有相应的产汇流水量平衡方程，即
为了避免斜线法、退水曲线法等传统基流分割方法带来的不确定性和主观性，时变增益模型采用国际上普遍认可和接收的数字滤波方法，将实测径流Q分割为地表径流Qs和地下径流Qg。
对于地表汇流过程，有地表水量平衡方程
进而，可采用最小二乘法估计出参数g3。
2.汇流模型参数识别
汇流参数包括瞬时单位线参数（n，K）和线性水库参数K KG。
传统的率定瞬时单位线的方法，是假定流域降雨径流系统为线性时不变系统的前提下，采用统计数学中的矩法来计算参数（n，K）。然而，利用矩法计算出的（n，K）得到的时段单位线进行洪水还原计算，会发现还原洪水过程与相应实测洪水过程（特别是洪峰点）的拟合误差较大，这在很大程度上限制了瞬时单位线的进一步应用。
传统的率定线性水库参数的方法，是从实测流量过程线中根据组合退水曲线识别洪水过程的退水段，确定退水曲线Qt=Q0·e-t/K的起始点（也即地表流量过程终止点）。根据退水曲线的递推形式Qt+1=e-t/K·Qt=Cg·Qt，可得Cg=Qt+1/Qt。选择多组退水过程观测值（Qt，Qt+1），利用最小二乘法可估计消退系数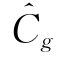
。但是，实测流量过程线的退水点很难确定，特别是在人类活动影响下，这种方法的精度将不能得到保证。
本模型采用目前应用最为广泛遗传算法（GA）和复合型进化算法（SCE-UA）来率定汇流三参数（n，K，K KG），以模拟流量和实测流量的残差平方和最小为目标函数，可很好地控制水量平衡、洪峰流量和流量过程线形状。
有关山东省水安全问题与适应对策：理论与实践的文章
- 详细阅读
-
河流水量平衡探讨详细阅读
科罗拉多河流域范围内的总调水量为该河河口段自然年径流量的30%。此外，许多供水河流的径流因当地的水利活动而变化。根据现已做出的预测，将来人类对河川径流的需求还要大大增加，例如，在科罗拉多河流域范围内，调水量已达70亿m3/a，约占该河自然水资源的1/3，而且这条河河口处的径流现在已接近完全用尽。在蒸发接近于蒸发率的多水地区，水资源区域再分配不应该对河流集水区多年水量平衡有任何较大的影响。......
2023-06-30
-
基于NAM模型的雁栖河流域降雨径流模拟与参数详细阅读
NAM模型通过给定降雨来模拟流域产流。根据雁栖河流域的流域特征和资料情况，降雨径流模型的时间步长设定为24小时。表2NAM模型率定参数表图2是雁栖河流域的柏崖厂水文站模拟和实测流量过程对比图，图中实线为模拟值，虚线为实测值，从降雨径流模拟结果可以看出，模型参数得到了较好的率定，模型模拟误差为0.642，见表3。......
2023-06-26
-
水量平衡公式及其应用分析详细阅读
3.计算分区地表水量平衡公式城市计算分区(地表水):式中:CRWt、CLWt、CXWt分别为水库对城市供水量、城市当地可供水量以及外流域或区域对城市供水量;CDt、CIt、CAt、CEt、COt分别为城市生活用水、城市工业用水、城市农业用水、城市生态环境用水和城市其他用水;CETt、CFTt分别为城市蒸发、城市渗漏水量;CRWt为城市退水;CCWt为城市重复利用水量。......
2023-06-30
-
电路参数计算方法：理论与实际的平衡详细阅读
在电路参数的计算中，精确的理论计算往往是不合实际的，由于元器件的离散性及受多方面因素的影响，只需进行粗略计算，确定电路参数的初选数值范围，而参数的准确数值要借助于计算机仿真实验来调整确定。这是一种设计计算的顺序，也是一种设计计算方法。......
2023-06-28
-
功率平衡方程式优化为：如何应用功率平衡方程式详细阅读
综上所述，异步电动机运行时从电源输入电功率P1到转轴上输出机械功率P2的全过程用功率平衡方程式表示为不难看出，在电力传动自动控制系统中，不论是采用直流电力传动，还是采用交流电力传动，系统的转矩和功率始终是保持平衡的，这是控制系统基本控制规律。......
2023-06-25
-
参数方程导数求解方式或者函数导数：参数方程求详细阅读
1）参数方程确定的函数的导数有时函数由参数方程来表示更方便且简单，如π）表示以R为半径、原点为圆心的上半圆周曲线.星形线的直角坐标方程为其参数方程为显然星形线的参数方程更为简单.一般地，设参数方程若t∈（α，β）时，x＝x（t），y＝y（t）都有连续的导数，且x′（t）≠0，可以证明x＝x（t）必有单值反函数t＝t（x），代入y＝y（t）中，得y＝y［t（x）］，因此在所给条件下，参数方程确定了y......
2023-11-19
-
颗粒流基本方程简介详细阅读
将φ 乘以Boltzmann方程的两边，对整个颗粒脉动速度空间积分，获得φ 的输运方程。因此，可以通过假设颗粒的速度分布函数获得颗粒流的应力和能量通量等的表达式，或者用统计平均的办法建立各类守恒型方程来描述颗粒流的平均运动。因此，需要通过一定假设，建立泥沙颗粒相的本构关系。......
2023-06-22
相关推荐