样本分布曲线也称为经验频率曲线,是指由实测样本资料绘制的频率曲线。并通过点群中心连成一条光滑曲线,即为水文变量的经验频率曲线。图X3.5某站年降水量经验频率曲线2.经验频率曲线应用中存在的问题数理统计理论研究表明,样本容量n很大时,经验分布趋于总体分布。......
2025-09-29
19世纪末期,英国生物学家皮尔逊通过对大量的物理、生物、经济等方面试验资料的分析研究,提出了13种随机变量的分布曲线,其中第Ⅲ型曲线被引入水文计算中,成为当今水文计算中常用的频率曲线线型。
X3.5.2.1 皮尔逊Ⅲ型分布的密度函数
皮尔逊Ⅲ型分布的密度函数为
式中 Γ(α)——α的伽玛函数;
α、β、a0——三个参数。
皮尔逊Ⅲ型分布密度曲线如图X3.7所示。
可以推证,这三个参数与总体的均值、变差系数、偏态系数具有下列关系
图X3.7 皮尔逊Ⅲ型密度曲线
a0是随机变量可能取得的最小值,故其密度曲线是一条一端有限一端无限的不对称单峰、正偏曲线。在水文资料中,如年降水量、洪峰流量等,都不可能出现负数,故a0必须大于或等于零,由![]() 得知,在水文频率计算中一般Cs≥2Cv。
得知,在水文频率计算中一般Cs≥2Cv。
a0是随机变量可能取得的最小值,故其密度曲线是一条一端有限一端无限的不对称单峰、正偏曲线。在水文资料中,如年降水量、洪峰流量等,都不可能出现负数,故a0必须大于或等于零,由![]() 得知,在水文频率计算中一般Cs≥2Cv。
得知,在水文频率计算中一般Cs≥2Cv。
显然,当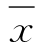 、Cv、Cs一定时,α、β、a0就唯一确定,因此,皮尔逊Ⅲ型分布的密度函数就完全确定了,则频率p=p(X≥xp)与xp的关系也就一一对应,如图X3.7所示,通过计算可确定其关系值。
、Cv、Cs一定时,α、β、a0就唯一确定,因此,皮尔逊Ⅲ型分布的密度函数就完全确定了,则频率p=p(X≥xp)与xp的关系也就一一对应,如图X3.7所示,通过计算可确定其关系值。
X3.5.2.2 皮尔逊Ⅲ型频率曲线——理论频率曲线的计算
由分布函数与密度函数的关系得
直接由式(X3.23)对给定的xP,进行积分计算p是非常麻烦的。因此,可将式(X3.23)进行变量代换计算,并将计算成果制成专用表,供实际工作查用。
1.离均系数Φp表
令
通常称Φ为离均系数或标准化变量,其均值为0,标准差为1。
对式(X3.23)引入离均系数Φ进行变量代换,整理后可得
显然,当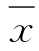 、Cv、Cs一定时,α、β、a0就唯一确定,因此,皮尔逊Ⅲ型分布的密度函数就完全确定了,则频率p=p(X≥xp)与xp的关系也就一一对应,如图X3.7所示,通过计算可确定其关系值。
、Cv、Cs一定时,α、β、a0就唯一确定,因此,皮尔逊Ⅲ型分布的密度函数就完全确定了,则频率p=p(X≥xp)与xp的关系也就一一对应,如图X3.7所示,通过计算可确定其关系值。
X3.5.2.2 皮尔逊Ⅲ型频率曲线——理论频率曲线的计算
由分布函数与密度函数的关系得
直接由式(X3.23)对给定的xP,进行积分计算p是非常麻烦的。因此,可将式(X3.23)进行变量代换计算,并将计算成果制成专用表,供实际工作查用。
1.离均系数Φp表
令
通常称Φ为离均系数或标准化变量,其均值为0,标准差为1。
对式(X3.23)引入离均系数Φ进行变量代换,整理后可得
这样经变换后,式(X3.25)的被积函数中只含一个统计参数Cs,其他两个参数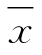 和Cv则包含在Φ中,因此只要给定一个Cs值,便可求得Φp与p的一一对应值。这一工作已先后由美国工程师福斯特和前苏联工程师雷布京完成,并制成了皮尔逊Ⅲ型曲线的离均系数Φp表,见附表1。
和Cv则包含在Φ中,因此只要给定一个Cs值,便可求得Φp与p的一一对应值。这一工作已先后由美国工程师福斯特和前苏联工程师雷布京完成,并制成了皮尔逊Ⅲ型曲线的离均系数Φp表,见附表1。
这样经变换后,式(X3.25)的被积函数中只含一个统计参数Cs,其他两个参数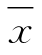 和Cv则包含在Φ中,因此只要给定一个Cs值,便可求得Φp与p的一一对应值。这一工作已先后由美国工程师福斯特和前苏联工程师雷布京完成,并制成了皮尔逊Ⅲ型曲线的离均系数Φp表,见附表1。
和Cv则包含在Φ中,因此只要给定一个Cs值,便可求得Φp与p的一一对应值。这一工作已先后由美国工程师福斯特和前苏联工程师雷布京完成,并制成了皮尔逊Ⅲ型曲线的离均系数Φp表,见附表1。
在频率计算时,当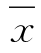 、Cv、Cs三个参数一定时,由已知的Cs值,利用附表1,可查得不同p所相应的Φp值,然后利用式(X3.24),由Φp即可求出不同p所相应的xp值,即
、Cv、Cs三个参数一定时,由已知的Cs值,利用附表1,可查得不同p所相应的Φp值,然后利用式(X3.24),由Φp即可求出不同p所相应的xp值,即
2.模比系数kp表
在频率计算时,当 、Cv、Cs三个参数一定时,由已知的Cs值,利用附表1,可查得不同p所相应的Φp值,然后利用式(X3.24),由Φp即可求出不同p所相应的xp值,即
、Cv、Cs三个参数一定时,由已知的Cs值,利用附表1,可查得不同p所相应的Φp值,然后利用式(X3.24),由Φp即可求出不同p所相应的xp值,即
2.模比系数kp表(https://www.chuimin.cn)
由模比系数的定义知,![]() ,则由式(X3.26)得kp=ΦpCv+1。为方便使用,利用离均系数Φp表,针对Cs等于Cv的一定倍数,已制成皮尔逊Ⅲ型曲线模比系数kp表,见附表2。使用时,只要根据给定的Cv及Cs(Cs以Cv的若干倍计),就可查得不同p相应的kp值,进而求出不同p相应的xp值,即
,则由式(X3.26)得kp=ΦpCv+1。为方便使用,利用离均系数Φp表,针对Cs等于Cv的一定倍数,已制成皮尔逊Ⅲ型曲线模比系数kp表,见附表2。使用时,只要根据给定的Cv及Cs(Cs以Cv的若干倍计),就可查得不同p相应的kp值,进而求出不同p相应的xp值,即![]()
有了一系列(p,xp)关系值,也称为理论点,由其即可绘制皮尔逊Ⅲ型分布的理论频率曲线。
由模比系数的定义知,![]() ,则由式(X3.26)得kp=ΦpCv+1。为方便使用,利用离均系数Φp表,针对Cs等于Cv的一定倍数,已制成皮尔逊Ⅲ型曲线模比系数kp表,见附表2。使用时,只要根据给定的Cv及Cs(Cs以Cv的若干倍计),就可查得不同p相应的kp值,进而求出不同p相应的xp值,即
,则由式(X3.26)得kp=ΦpCv+1。为方便使用,利用离均系数Φp表,针对Cs等于Cv的一定倍数,已制成皮尔逊Ⅲ型曲线模比系数kp表,见附表2。使用时,只要根据给定的Cv及Cs(Cs以Cv的若干倍计),就可查得不同p相应的kp值,进而求出不同p相应的xp值,即![]()
有了一系列(p,xp)关系值,也称为理论点,由其即可绘制皮尔逊Ⅲ型分布的理论频率曲线。
【例X3.3】 已知某地多年平均年降水量 =1000mm,Cv=0.5,Cs=2Cv=1.0,若年降水量的分布符合皮尔逊Ⅲ型,试求p=1%的年降水量。
=1000mm,Cv=0.5,Cs=2Cv=1.0,若年降水量的分布符合皮尔逊Ⅲ型,试求p=1%的年降水量。
由Cs=1.0、p=1%查附表1得Φp=3.02,利用式(X3.26)得
或由Cv=0.5,Cs=2Cv,p=1%查附表2,得kp=2.51,则
X3.5.2.3 统计参数对皮尔逊Ⅲ型频率曲线的影响
【例X3.3】 已知某地多年平均年降水量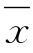 =1000mm,Cv=0.5,Cs=2Cv=1.0,若年降水量的分布符合皮尔逊Ⅲ型,试求p=1%的年降水量。
=1000mm,Cv=0.5,Cs=2Cv=1.0,若年降水量的分布符合皮尔逊Ⅲ型,试求p=1%的年降水量。
由Cs=1.0、p=1%查附表1得Φp=3.02,利用式(X3.26)得
或由Cv=0.5,Cs=2Cv,p=1%查附表2,得kp=2.51,则
X3.5.2.3 统计参数对皮尔逊Ⅲ型频率曲线的影响
1.均值 对频率曲线的影响
对频率曲线的影响
1.均值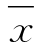 对频率曲线的影响
对频率曲线的影响
当皮尔逊Ⅲ型频率曲线的参数Cv和Cs值一定时,则相应的模比系数的频率曲线唯一确定。由![]() 可知,
可知,![]() 愈大,频率曲线的位置愈高,且均值大的频率曲线比均值小的频率曲线要陡,如图X3.8所示。
愈大,频率曲线的位置愈高,且均值大的频率曲线比均值小的频率曲线要陡,如图X3.8所示。
图X3.8 均值变化对频率曲线的影响
图X3.9 Cv变化对频率曲线的影响
2.变差系数Cv对频率曲线的影响
为了消除均值的影响,以模比系数k为变量绘制频率曲线,如图X3.9所示(图中Cs=1.0)。当Cv=0时,说明随机变量的取值都等于均值,故频率曲线即为k=1的一条水平线。Cv越大,说明随机变量相对于均值越离散,因而频率曲线将越偏离k=1的水平线。Cs一定时,不同Cv值的模比系数的频率曲线交于纵坐标k=1的一点,随着Cv的增大,频率曲线显得越来越陡。
图X3.10 Cs变化对频率曲线的影响
3.偏态系数Cs对频率曲线的影响
对于正态分布Cs=0,频率曲线绘在频率格纸上为一条直线。水文特征值的统计规律一般为正偏,在正偏情况下,曲线向上凹。当Cv一定时,以模比系数k为变量绘制的频率曲线,Cs值越大,曲线凹势越显著,即频率曲线的上端变陡而下端变平,曲线越弯曲,如图X3.10所示;反之,Cs值减少,则曲线凹势变小。
当皮尔逊Ⅲ型频率曲线的参数Cv和Cs值一定时,则相应的模比系数的频率曲线唯一确定。由![]() 可知,
可知,![]() 愈大,频率曲线的位置愈高,且均值大的频率曲线比均值小的频率曲线要陡,如图X3.8所示。
愈大,频率曲线的位置愈高,且均值大的频率曲线比均值小的频率曲线要陡,如图X3.8所示。
图X3.8 均值变化对频率曲线的影响
图X3.9 Cv变化对频率曲线的影响
2.变差系数Cv对频率曲线的影响
为了消除均值的影响,以模比系数k为变量绘制频率曲线,如图X3.9所示(图中Cs=1.0)。当Cv=0时,说明随机变量的取值都等于均值,故频率曲线即为k=1的一条水平线。Cv越大,说明随机变量相对于均值越离散,因而频率曲线将越偏离k=1的水平线。Cs一定时,不同Cv值的模比系数的频率曲线交于纵坐标k=1的一点,随着Cv的增大,频率曲线显得越来越陡。
图X3.10 Cs变化对频率曲线的影响
3.偏态系数Cs对频率曲线的影响
对于正态分布Cs=0,频率曲线绘在频率格纸上为一条直线。水文特征值的统计规律一般为正偏,在正偏情况下,曲线向上凹。当Cv一定时,以模比系数k为变量绘制的频率曲线,Cs值越大,曲线凹势越显著,即频率曲线的上端变陡而下端变平,曲线越弯曲,如图X3.10所示;反之,Cs值减少,则曲线凹势变小。
相关文章

样本分布曲线也称为经验频率曲线,是指由实测样本资料绘制的频率曲线。并通过点群中心连成一条光滑曲线,即为水文变量的经验频率曲线。图X3.5某站年降水量经验频率曲线2.经验频率曲线应用中存在的问题数理统计理论研究表明,样本容量n很大时,经验分布趋于总体分布。......
2025-09-29

重载型自动扶梯在国内外的公共交通建设中得到广泛使用,目的是希望自动扶梯能适应地铁等大客流公共交通场所恶劣的使用环境。可见美国的公共交通运输系统采用重载型自动扶梯的目的与我们是相同的。伦敦地铁是最早采用重载型自动扶梯的地铁,也是对自动扶梯的使用有深刻认识的地铁企业。自动扶梯经受了大客流、强载荷的使用考验。城市轨道交通的大规模发展,对重载型自动扶梯必然出现更大的需求。......
2025-09-29

曲线的曲率用于描述曲线偏离直线的程度,一般是用曲线上某点的切线方向角对弧长的转动率进行描述。直观地说,曲率用来描述某一曲线的弯曲程度,并且曲率越高曲线的弯曲程度也越高。曲率图中的下凹和上凸表示曲线形状发生了快速变化;曲率图中的拐角或弯折并不表示曲线中的弯折,仅仅表示曲率的急剧变化,曲线斜率仍然内部连续。曲率图是交互式的,随曲线的修改而更新,可改变初图曲线段的数量、图的相对尺寸和曲率类型。......
2025-09-29

实操目的1.通过观察,认知交、直流接触器的外观。实操用器材、仪表及工具1.交流接触器1只;2.直流接触器1只;3.万用表1只;4.电工工具1套。......
2025-09-29

光滤波器也与此类似,它是光通信系统,特别是WDM网络中非常重要的器件。图3-4给出可调谐光滤波器的基本功能,图中Δfs为输入的最高频率信道和最低频率信道之间的频率差,Δfch为信道间隔。图3-4 可调谐光滤波器的基本功能在WDM系统中,每个接收机都必须选择所需要的信道。若采用相干检测,则要求有可调谐本地振荡器;若采用直接检测,则要求在接收机前放置可调谐光滤波器。......
2025-09-29

干涉型光谱仪是利用光的干涉原理进行工作的,干涉仪主要有迈克耳逊干涉仪和法布里—珀罗干涉仪。由于常用的干涉型光谱仪为傅立叶变换拉曼光谱仪。迈克耳逊干涉仪是傅立叶变换光谱仪的核心部件,它的结构如图5-7所示。探测到的干涉光信号经放大后在数据处理系统进行傅立叶变换,即获得光源的光谱图。......
2025-09-29

可在一个曲面、曲线或模型边线上的任意位置创建基准点而无需进行尺寸定位,这样的基准点称为域点。图3.1.18 域点2.域点的应用练习要求:打开图3.1.19所示的reverse_block.prt零件模型,在螺旋特征上的某一位置创建一个基准点。Step2.单击“点”按钮中的。Step3.在图3.1.19所示的螺旋特征的边线上单击,系统立即创建基准点。......
2025-09-29

图3.3.20 由曲面边界创建基准曲线图3.3.21 选中曲面的一条边线Step3.选择下拉菜单命令,出现操控板,如图3.3.22所示。图3.3.22 “偏移”操控板注意:当选取的曲面边界为单条时,操控板的“量度”界面中的“距离类型”通常有下列选项,如图3.3.23所示。图3.3.23 “量度”界面Step5.在操控板的“量度”界面中的空白处右击,选择命令,可增加新的偏距条目。......
2025-09-29
相关推荐