BET氮吸附在应用中的作用

2023-06-20 理论教育版权反馈

【摘要】：例如BET比表面积只是对氮吸附等温线中P／P0=0.05～0.35之间的一小段用经典的BET公式处理了一下，得到单层吸附量数据Vm，然后据此算出比表面积的。H3与H4相比高压端吸附量更大，认为是片状粒子堆积形成的狭缝孔。图9-11SBA-15样品的典型等温吸附曲线及计算得到的孔径分布下面以SBA-15分子筛为例，介绍介孔材料的吸附等温线和介孔尺寸分布［8，9］。

利用氮气吸附装置可以得到样品的多种性能，包括样品的吸附／脱附等温线、比表面积、孔径分布、孔容、真实固体密度、堆密度等等，更换吸附气体还可以研究样品的化学吸附性能。但我们要明确一点，利用氮气吸附装置获得的数据中，只有吸附／脱附等温线是真实可靠的，其他性能都是利用相关理论建模和计算得到的。例如BET比表面积只是对氮吸附等温线中P／P0=0.05～0.35之间的一小段用经典的BET公式（9-17）处理了一下，得到单层吸附量数据Vm，然后据此算出比表面积的。因此在利用氮吸附装置研究比表面积或孔材料性能时，选择合适的计算模型和公式是至关重要的。

1.纳米材料比表面积

氮吸附最广泛且最基本的应用就是研究材料的比表面积，目前大部分的氮吸附仪器都集成了BET比表面积和Langmuir比表面积公式的软件，完成吸附／脱附等温线后，点击相应计算软件即可直接获得纳米材料的比表面积数值（如图9-9所示）。

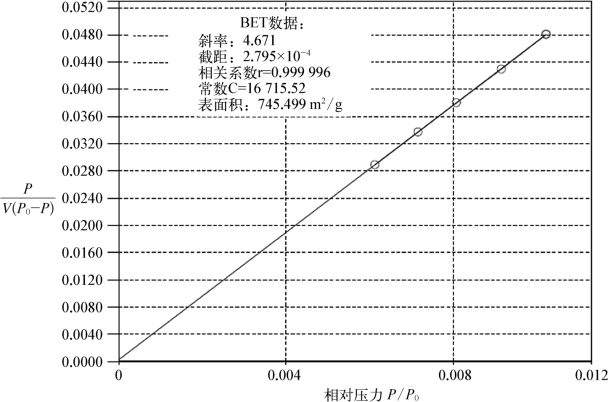
pagenumber_ebook=236,pagenumber_book=228

图9-9　美国康塔公司氮吸附仪器给出的测量图

所以，在研究纳米材料的比表面积时，相关研究只给出所研究材料的比表面积数值即可，而不会同时提供氮吸附曲线［7］。

2.纳米介孔材料研究

从前面的等温吸附曲线类型可以知道，介孔材料的吸附曲线类型为Ⅳ型，在吸附／脱附曲线中会出现滞后环；滞后环的产生是由于毛细管力的作用。滞后环的特征对应于特定的孔结构信息。根据滞后环的形状可将其分为四大类，如图9-10所示。

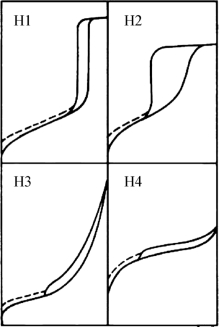
pagenumber_ebook=236,pagenumber_book=228

图9-10　介孔材料等温吸附曲线中的滞后环类型

（1）H1是均匀孔模型，可视为直筒孔。H1型滞后环可以看出为十分有序介孔。

（2）H2比较难解释，一般认为是多孔吸附质或均匀粒子堆积孔造成的，多认为是“ink bottle”，等小孔径瓶颈中的液氮脱附后，束缚于瓶中的液氮气体会骤然逸出。

（3）H3与H4相比高压端吸附量更大，认为是片状粒子堆积形成的狭缝孔。

（4）H4也是狭缝孔，但区别于粒子堆集，是一些类似由层状结构产生的孔。

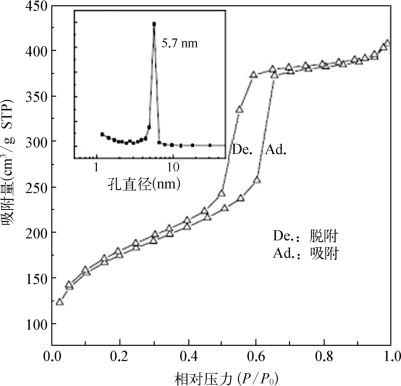
pagenumber_ebook=237,pagenumber_book=229

图9-11　SBA-15样品的典型等温吸附曲线及计算得到的孔径分布

下面以SBA-15分子筛为例，介绍介孔材料的吸附等温线和介孔尺寸分布［8，9］。图9-11中为SBA-15为典型的等温吸附曲线，线旁Ad代表吸收曲线，De代表脱附曲线；小图中为由样品的等温吸附曲线计算出的孔径分布。图中所示的等温线属于IUPAC分类中的IV型，H1滞后环。从图9-12中可看出，在低压段吸附量平缓增加，此时N2分子以单层到多层的方式吸附在介孔的内表面，所以对有序介孔材料用BET方法计算比表面积时应取相对压力P／P0=0.10～0.29比较适合。在P／P0=0.5～0.8左右吸附量有一突增。该段的位置反映了样品孔径的大小，其变化宽窄可作为衡量中孔均一性的根据。在更高P／P0时可能会出现第三段上升，可以反映出样品中大孔或粒子堆积孔情况。所以利用N2吸脱附等温线可以测定介孔材料的比表面积、孔容和孔径分布。一般来说，对比表面积的分析采用BET（Brunauer-Emmett-Teller）方法；孔径分布的计算采用BJH（Barrett-Joiner-Halenda）模型。

除N2外，还可选择Ar、CO2、甲烷等气体作为吸附剂，这主要取决于样品对气体的吸附性质和所需获得的信息。如对于某种沸石化合物框架结构的样品，在同样的吸附条件下，对CO2的吸附量明显大于对N2和CH4的吸附量（见图9-12）。选择不同的吸附气体除了可以研究样品的选择吸附和孔径，也可研究相关样品的化学吸附性质。

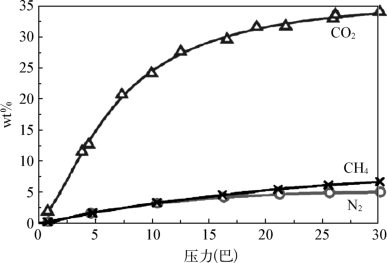
pagenumber_ebook=237,pagenumber_book=229

图9-12　nZIF-8样品在不同吸附气体下的等温吸附曲线［10］

每一种计算公式都有其计算模型，即都进行了一定的假设［11］。当研究对象改变后，原有的理论模型和公式都不再适用。因此，研究介孔的计算公式用于研究微孔材料时必然会出现较大的误差，需要寻找新的模型和计算公式。例如使用传统的BJH法计算模板孔径分子筛MCM41时，会与NLDFT方法的计算结果相差25%，如图9-13所示。

pagenumber_ebook=238,pagenumber_book=230

图9-13　MCM41样品的等温吸附曲线及孔径计算结果［11］

（a）MCM41分子筛的77 K氮吸附／脱附等温线（实验曲线与NLDFT拟合等温线的比较）
（b）从N2／MCM-41等温线计算得到的孔径分布曲线（分别应用NLDFT和BJH法）

非线性密度泛涵理论（NLDFT）是基于密度函数理论（DFT）和分子模拟方法（MC，蒙特卡洛模拟方法）的一种改进理论。相对于那些上述其他研究方法，密度函数理论（DFT）和分子模拟方法（MC，蒙特卡洛模拟方法）是分子动力学方法。它们不仅提供了吸附的微观模型而且更真实地反映了孔中流体的热力学性质。在计算过程中考虑并计算了吸附在表面的流体和在孔里的流体的平衡密度分布，进而推导出模型体系的吸附／脱附等温线、吸附热、中子散射方式和转移特性。密度分布是通过MC模拟和DFT理论，计算了分子间流体—流体间和流体—固体间相互作用获得的。流体—流体相互作用的参数是通过再生他们的宏观整体性质测定的（如低温下氮和氩的性质）。固体—流体间相互作用的参数则是通过计算拟合在平滑表面上标准氮和氩的吸附等温线获得的。

3.纳米微孔材料研究

图9-14所示为一个同时含有微孔和介孔的样品的典型等温吸附曲线，从中可以看到，开口和闭口介孔的滞后环虽然发生在不同的相对压力下，但可供分析的相对压力都处于0.4～0.6的正常压力范围，可以用传统的氮吸附实验进行分析；但微孔的分析数据在相对压力很低的范围，而一般的氮吸附实验的相对压力都从犘／犘0＞0.01左右开始测试，但这时微孔已经被填充，所以无法得到相关的微孔尺寸信息。对于微孔材料的氮吸附需要采用高精度、低压吸附装置，犘／犘0的变化范围为10-6或10-7到1。在沸石材料的研究中场使用Ar气作为低压吸附气体。所以含微孔材料的微孔分析对真空度，控制系统，温度传感器有不同的要求，测试时间也比较长，时间可能是普通样品的十倍甚至二十倍。由于微孔尺寸和探针分子大小相差有限，部分微孔探针分子尚不能进入，解析方法要根据不同的样品来定，需要时可借鉴相关文献方法来参考，再则自己做一批样品采用的是一种分析方法，结果的趋势多半是正确的［13-18］。

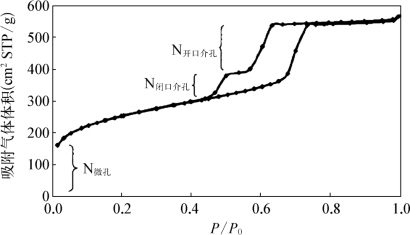
pagenumber_ebook=239,pagenumber_book=231

图9-14　同时含有微孔和介孔样品的等温吸附曲线［12］

同样，BJH只适用于中孔（＞5 nm）材料，而对微孔进行计算时会有很大的误差，需要采用更高精度的计算模型和公式。如对于缝型孔，可使用KJS（Kruk-Jaroniec-Sayari）及其修正方法，KJS刚开始主要用于高度有序的MCM-41材料的孔分析，结合XRD结果，可得出比BJH有更高精度的孔径，适用孔径分析范围在2～6.5 nm之间。后来又对其进行了修正及改进，使之有了更大的适用范围。对于圆柱状介孔，SF（Saito-Foley）模型更加适用。

此外，还可使用t--Plot对等温吸附曲线进行分析。它们都是对整条吸附或脱附曲线的处理方法，t-Plot和αs-Plot以氮气吸附量对单分子层吸附量作图，凝聚时形成的吸附膜平均厚度是平均吸附层数乘以单分子层厚度（0.354 nm）。样品为无孔材料时，t-Plot是一条过原点直线，当试样中含有微孔、介孔或大孔时，直线就会变成几段折线（如图9-15所示），需要分别分析。αs-Plot方法中的下标是standard的意思，用相对压力为0.4时的吸附量代替单分子层吸附量，再去作图，用这种方法先要指定一个标准，或是在仪器上做一个标样，处理方法和图形解释两种方法是类似的。两者之间可以相互转化，t=0.538αs。

pagenumber_ebook=240,pagenumber_book=232

图9-15　无孔、介孔、微孔和微介孔样品的t-Plot曲线［19］

BET氮吸附在应用中的作用

相关推荐