罗巴切夫斯基几何的发展与争议

2025-09-30 理论教育版权反馈

【摘要】：罗巴切夫斯基明确指出,这些定理并不包含矛盾,因而其总体形成了一个逻辑上可能的、无矛盾的理论,这个理论就是罗巴切夫斯基几何。而欧几里得几何仅是罗巴切夫斯基几何的特例。正因如此,罗巴切夫斯基几何在提出后的相当长一段时间内,乃至罗巴切夫斯基去世后的30 年内,不但未能赢得社会的承认和赞美,反而遭到种种非难和攻击,致使非欧几何这一新理论迟迟得不到学术界的公认。

罗巴切夫斯基自1815 年开始研究平行线理论,最初是遵循着前人的探讨思路,试图给出平行公设的证明。可很快他便意识到自己的思路和证明是错误的。前人和自己的失败启迪了他,使其大胆提出了相反的猜测:可能根本就不存在平行公设的证明。于是他便调转思路,着手寻求平行公设不可证的解答。这是一个全新的,也是与传统思路完全相反的探索途径。正是沿着这个途径,罗巴切夫斯基发现了一个崭新的几何世界。

pagenumber_ebook=66,pagenumber_book=57

图1.10.1　罗巴切夫斯基

1826 年2 月23 日,罗巴切夫斯基在喀山大学物理数学系学术会议上,宣读了其第一篇关于非欧几何的论文《几何学原理及平行线定理严格证明之摘要》。这篇首创性论文的问世,标志着非欧几何的诞生。

当时,参加学术会议的全是数学造诣较深的专家,其中有著名的数学家、天文学家西蒙诺夫(A.M.Cимонов),有后来成为科学院院士的古普费尔以及后来在数学界颇有声望的博拉斯曼。然而他们对罗巴切夫斯基的观点保持了沉默,故可谓新几何在冷漠中宣告诞生。尽管如此,罗巴切夫斯基毫不气馁,继续坚持自己的研究:1829 年写下了《几何学原理》,1835 ～1837 年间写下了《具有平行的完全理论的几何新基础》,1840 以德文发表《平行理论的几何研究》,1855 撰写了《泛几何学》等。

罗巴切夫斯基的基本思想与高斯、波尔约(匈牙利数学家)的基本一致,即用与欧氏第五公设相反的断言“通过直线外一点,可引不止一条即至少两条直线与已知直线不相交”作为替代公设,由此出发进行逻辑推导而得出一系列新几何学的定理。罗巴切夫斯基明确指出,这些定理并不包含矛盾,因而其总体形成了一个逻辑上可能的、无矛盾的理论,这个理论就是罗巴切夫斯基几何。而欧几里得几何仅是罗巴切夫斯基几何的特例。

表1.10.1　欧几里得几何和罗巴切夫斯基几何的比较(https://www.chuimin.cn)

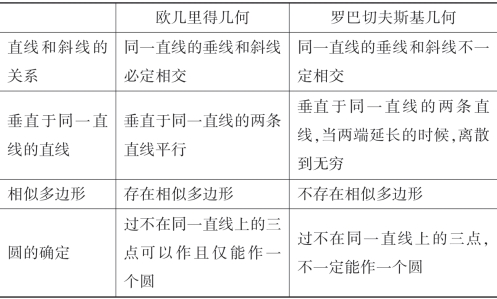
pagenumber_ebook=67,pagenumber_book=58