欧氏空间中的对称变换及其性质

2023-11-22 理论教育版权反馈

【摘要】：设V是n维欧氏空间，如果线性变换σ：V→V在一组标准正交基下的矩阵是对称矩阵，则称该线性变换为对称变换.定理6.6 欧氏空间中的线性变换σ是对称变换的充分必要条件是对任意的向量α，β，有<σ（α），β>=<α，σ（β）>.证明：必要性，若σ是对称变换，在标准正交基ε1，ε2，…

设V是n维欧氏空间，如果线性变换σ：V→V在一组标准正交基下的矩阵是对称矩阵，则称该线性变换为对称变换.

定理6.6 欧氏空间中的线性变换σ是对称变换的充分必要条件是对任意的向量α，β，有

<σ（α），β>=<α，σ（β）>.

证明：必要性，若σ是对称变换，在标准正交基ε₁，ε₂，…，ε_n下的矩阵是A，A^T=A.设α，β在这组标准正交基之下的坐标是x，y，则有

<σ（α），β>=（Ax）^Ty=x^T（Ay）=<α，σ（β）>.

充分性，由于

<σ（α），β>=（Ax）^Ty=x^TA^Ty

及

<α，σ（β）>=x^TAy，

因此有x^T（A^T-A）y=0对任意的x，y都成立，则A^T-A=0.证毕.

定理6.7 对称变换的特征值均为实数.

证明：只要证明对称矩阵A的特征值都是实数即可.

设λ是对称矩阵A的特征值，非零向量x是属于λ的特征向量，则

Ax=λx.

取共轭复数有

下面用两种方法计算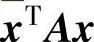，得到

由于x≠0，因此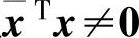，比较两式得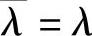，即λ是实数.证毕.

定理6.8 属于对称变换的不同特征值的特征向量一定是正交的.

证明：设λ₁≠λ₂是对称变换σ的两个不同的特征值，α，β分别是属于它们的特征向量，即

σ（α）=λ₁α，σ（β）=λ₂β，λ₁=λ₂，

那么就有

<σ（α），β>=<λ₁α，β>=λ₁<α，β>，

<σ（α），β>=<α，σ（β）>=<α，λ₂β>=λ₂<α，β>，

比较得<α，β>=0.证毕.(www.chuimin.cn)

定理6.9 若σ是对称变换，则一定存在一组标准正交基，使得σ在这组基下的矩阵是对角形矩阵.

证明：对欧氏空间V的维数n用归纳法.

当n=1时，显然成立.现在假设对维数不超过n-1的欧氏空间命题都成立.

对n维欧氏空间.设λ₁是其上对称变换σ的一个特征值，ε₁，ε₂，…，ε_s是特征子空间V_λ1的一组标准正交基，则

σ（ε_i）=λ₁ε_i，1≤i≤s.

将这组V_λ1的标准正交基扩充为V的标准正交基ε₁，ε₂，…，ε_n.并记

W=span（ε_s+1，…，ε_n），

记σ在W上的限制为τ=σ|_W，则W的维数是n-s<n，且

<τ（ε_i），ε_j>=<σ（ε_i），ε_j>=<ε_i，σ（ε_j）>=<ε_i，τ（ε_j）>，

即τ是对称变换.由归纳假设，在子空间W中一定存在一组标准正交基ε′_s+1，ε′_s+2，…，ε′_n，满足条件τ（ε′_i）=λ_iε′_i，即σ（ε′_i）=λ_iε′_i，s+1≤i≤n.

取ε′_i=ε_i，1≤i≤s，则向量组ε′₁，ε′₂，…，ε′_n是V的一组标准正交基，且

σ（ε′_i）=λ_iε′_i，1≤i≤n.

证毕.

定理6.7～定理6.9用矩阵的语言叙述就是：

定理6.10 实对称矩阵的特征值都是实数，且属于不同特征值的特征向量一定是正交的.

定理6.11 实对称矩阵一定正交相似（或合同）于一个对角形矩阵.

习题

6.5.1. 设A是秩为r的n阶对称幂等矩阵，证明：存在正交矩阵O，使得

6.5.2. 设A是n阶对称对合矩阵，证明：存在正交矩阵O，使得

6.5.3. 设A是n阶对称矩阵，利用矩阵的方法证明：

（1）A的特征值都是实数；

（2）A的属于不同特征值的特征向量一定是正交的；

（3）A正交合同（相似）于对角阵.

欧氏空间中的对称变换及其性质

相关推荐