魔鬼物理学2:团结如蜜蜂的玻色子

伯特·荷尔多布勒与爱德华·威尔逊在《超个体：昆虫社会的美丽、优雅和奇妙》一书中提出，黄蜂、蚂蚁、蜜蜂或者白蚁的聚居地（巢穴），可以被整体地视为一个动物体。他们认为，每一只昆虫都是“超个体”中的一个类似“细胞”的成分：觅食者是眼睛和感觉器官，守卫者们起到免疫系统的作用，蚁后（蜂后）则扮演生殖器官的角色。“超个体”和普通动物之间的一个最重要的区别在于，前者缺少作为核心的大脑或神经系统。然而，每个聚居地内部都通过昆虫间的交互规则来管理它的组织和规模，由此聚居地可以达到远超单只昆虫能力的发展水平。正如通俗科幻小说的读者所知道的那样，这也是人类击败外星人侵略的手段（或者至少是其中的一种手段）。

西奥多·斯特金的科幻小说《宇宙掠夺》（The Cosmic Rape）于1958年出版，与此同时，小说的删节版在《银河杂志》（Galaxy）上发表，题为“与美杜莎相会”（To Marry Medusa）。故事中，外星智慧生命采取了非常规的手段来征服地球。外星人实际上是一个宇宙孢子，能够控制人类个体的心智。它惊奇地发现，尽管地球这颗行星被建筑物、桥梁、公路等复杂的结构所覆盖，地球人之间并不存在精神上的连接。根据孢子征服其他行星的过往经验，只在独立个体的原始智慧以一种协作的方式思考，就像一群蚂蚁或蜜蜂那样，才能建造出地球上的各种高级基础设施。入侵的孢子从未遇到哪个物种的个体可以独立设计桥梁或建筑物，孢子因此推断，地球人之间曾经存在的集体连接已经被切断。于是，孢子制订了一个重新建立连接的计划，让所有的地球人同步思考和工作。它的计划成功了，但对于外星生命体而言却是不幸的。当它发现自己不是在对付一个人的心智，而是几十亿人的集体意识时，人类的“蜂群思维”迅速策划了一个有效的反击计划，摧毁了外星孢子的入侵。斯特金用这种方式描述了玻色—爱因斯坦凝聚态的合作行为。

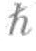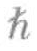在斯特金的小说中，外星孢子创造了人类的宏观量子态，单个波函数包含了关于其组成元素的全部信息。任何一个元素，也就是斯特金小说中的一个人，他的变化都会被立刻传输给波函数中的所有其他元素，即小说中其余的人。这种情形在现实世界中频繁发生，表现为超导体中成对电子间的量子相互作用或超流体中氦原子间的相互作用。这些发生凝聚的粒子，其内禀角动量值是而不是/2的倍数。内禀角动量值为的整数倍的粒子被称为玻色子，它们遵循萨蒂延德拉·玻色和阿尔伯特·爱因斯坦创建的一种量子统计方式——“玻色—爱因斯坦统计”。

在前一章中我们讨论了费米子，费米子的内禀角动量值可以为+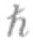/2或-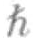/2，但不可以是任何其他值。这从本质上来讲是不对称的，因为我们可以对一个顺时针旋转和一个逆时针旋转进行区分。当两个费米子之间的距离很近以至于它们的波函数发生重叠时，我们用一面黑、一面白的色带来表示这种情况。这两种颜色的意义在于，我们可以轻而易举地分辨出内禀角动量值为+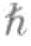/2和内禀角动量值为-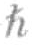/2的电子，就像我们可以轻易地分辨出色带的黑面和白面。但是，实验已经揭示出在一些情况下，内禀角动量的值可以取0、或2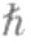，等等，而不可以取任何分数值。我们首先考虑内禀角动量值为零的量子物质的情况，再考虑内禀角动量值为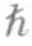的粒子，比如光子。

作为原子的基本组成部分，电子、质子、中子均为费米子，什么样的物质内禀角动量值会是零呢？氦原子便是一个例子。一个氦原子核内包含两个质子和两个中子，每一个粒子的内禀角动量值为+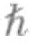/2或-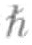/2。由于两个质子是全同的，当它们在原子核中处于最低能量态时，它们会以+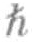/2和-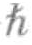/2配成对，因而总的内禀角动量值为零，两个全同中子的情况与之类似。同样，如图12-3（b）所示，两个电子也是配对的。综上所述，当处于最低能量态时，一个氦原子的总内禀角动量值为零。

内禀角动量值为零的粒子是对称的，在这种情况下我们不能用顺时针或逆时针来描述它的自旋。当两个这样的粒子彼此靠近，它们的波函数发生重叠时，我们将用一条两面皆为白色的色带来表示它们。我再强调一次，色带用来比喻双粒子波函数，因此我们将忽略一些问题，因为它们只会导致我们偏离现在的讨论。

让我们重复一下第12章的色带实验，只不过我们现在使用的是一条两面同色的色带，比如白色（图13-1）。我抓住它的两端，而且很明显，色带的白面朝外［图13-1（a）］。接下来，我互换两端的位置，左边的一端现在在右边，就像第12章那样，这一过程使色带扭转了半圈［图13-1（b）］。当然，色带现在仍然是白面朝外。我可以通过翻转色带的一端来消除扭结，这样背面将转到外面［图13-1（c）］。当色带的一面是黑色而另一面是白色时，这是一个禁阻操作，因为它改变了色带的状态（色带的两端原来都是白面朝外，操作后会有一端是黑面朝外）。但是，如果色带的两面都是白色的，这个对称性意味着我能够翻转色带的一端以消除扭结，而且不改变其他任何事情。重点在于，白色的色带经过一次翻转就可以回到它本来的状态，而黑—白色带则需要两次翻转才能恢复原状。

图13-1　图a为两面同色的色带示意图。交换色带两端将使色带扭转半圈（图b），旋转色带一端可以将扭结解除（图c），使色带恢复原状

这种对称性表明，内禀角动量值为零的粒子（如氦原子），以及内禀角动量值为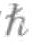的光子，都被称为玻色子，它们的行为可以用双粒子波函数来表示，写作两个函数A和B之和，即Ψ=A+B，而不是费米子的Ψ=A-B。[1]与之前相同，A和B是在位置1和2处的单粒子波函数的乘积。如果粒子1和粒子2交换位置，双粒子波函数Ψ=A+B的值保持不变，但此时Ψ将表示为Ψ=B+A。因此，Ψ=A+B=B+A。当内禀角动量值为零或者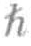的两个粒子彼此靠近，它们的物质波发生重叠时，产生的双粒子波函数的值取决于单粒子波函数的值。

将双粒子波函数写作Ψ=A+B会产生什么结果呢？让我们来回顾一下，对于像电子这样的费米子，其双电子波函数为Ψ=A-B，这意味着两个电子都处于相同量子态（即A=B）的概率为零。对于玻色子而言，Ψ=A+B表明两个粒子处于相同量子态（即A=B）的概率很高。因为当A=B时，有Ψ=A+A=2A，且概率密度Ψ2=2A×2A=4A2。对于一个处于Ψ=A量子态的单独粒子，其概率密度为Ψ2=A×A=A2，两个单独粒子的概率密度为Ψ2=A2+A2=2A2。因此，只要在第一个粒子附近引入第二个粒子，它们都处于A量子态的概率是两个单独粒子同处量子态A时概率的两倍。尽管两个粒子处于相同量子态的概率不是100％，但与单粒子的情形相比，概率已经有所提高。两个粒子处于相同位置并具有相同量子态的概率更高，表明这种情况更有可能发生。

当一个系统的温度降低时，粒子就会沉降至较低的能量态。如果粒子可以通过某种方式加以区分，比如它们的波函数不发生重叠，我们就不需要考虑费米—狄拉克统计或玻色—爱因斯坦统计。而且我们会发现，在较低温度条件下，有些粒子处于最低能量态，有些处于次低能量态，有些处于较高能量态，而处于很高能量态的粒子数目可以忽略不计。对于费米子，比如固体中的电子，无论温度高低，仅有两个电子可以占据最低能量态（一个内禀角动量值为+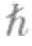/2，另一个内禀角动量值为-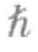/2）。与可辨识粒子的情况相比，玻色子在低温条件下集中处于最低能量态（基态）的概率更高。对于玻色子，在每个位置和每个自旋方向上仅能有一个粒子的规则不再适用，很多粒子可以处于相同能量态。这些内禀角动量值为零或者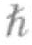的粒子遵循玻色—爱因斯坦统计规则，这种聚集于基态的现象被称为“玻色—爱因斯坦凝聚态”。

为什么在低温条件下才能观察到这种凝聚态？如果粒子间相距甚远，那么它们的波函数几乎不会发生重叠，所有关于“不可辨识粒子”的问题也与此无关。温度计只是用来跟踪记录每个粒子平均能量的装置，能量越低，粒子的动能越低，动量也越小。根据德布罗意关系式，一个较小的动量对应一个较长的物质波。如果涉及的粒子的物质波较长，不同的全同粒子的物质波之间就更容易发生重叠。类似地，将粒子限定在一个小区域内也会增加波函数相互作用的概率。因此，低温和小区域（通过高压来实现）有助于形成玻色—爱因斯坦凝聚态。

玻色—爱因斯坦凝聚态有哪些特殊属性呢？我们已经考察了两个全同玻色子的情况，它们的波函数重叠使得它们可以用一个双电子波函数来表示。随着气相玻色子的温度降低，数百万个全同原子的波函数发生重叠，全部处于相同的量子态。我们因此得到了一个能描述数百万个原子行为的单一波函数。通过这种方式，难以辨识的玻色子们表现得像一个统一体，无论一个原子发生了什么情况，都会复制到其他原子上。玻色—爱因斯坦凝聚态与1960年的科幻电影《魔童村》（Village of the Damned）中被魔鬼占据身体的小孩们如出一辙：皮肤白皙、金发碧眼的孩子们相当于玻色—爱因斯坦凝聚态下的全同粒子，电影中一个孩子习得的知识可立即与其他所有孩子共享的事实，则是描述这种凝聚态的多粒子波函数作用的必然结果。

1995年，美国物理学家埃里克·康奈尔和卡尔·韦曼，以及德国物理学家沃夫冈·克特勒分别在实验中直接观测到真正的凝聚态，从而证实了玻色和爱因斯坦在1925年的理论预测。他们因这项成就而共同获得2001年的诺贝尔物理学奖。他们在研究中使用了数千个铷或钠的同位素，并将它们冷却到高于热力学绝对零度的百万分之一开氏度。因为玻色—爱因斯坦凝聚态是短暂的量子物质，因此不易获得或被观察到。然而，现实世界中还存在更强大的系统，它们具有将玻色子凝聚成一个低能量子态的突出特性。

如前所述，氦原子的总内禀角动量值为零，是玻色子。氦原子中的两个基态电子处于配对状态［图12-3（b）］，因此氦原子不与其他原子发生化学上的强相互作用。氦的这一特性，即电子成对地填满“整行”轨道，与氖、氩等其他一些元素相同，它们被称为惰性或稀有气体。这些元素一直保持气态，直到温度极低时，电荷排布上的微小振荡在原子间产生了微弱的静电吸引力。氦原子间的相互作用太弱，直到比绝对零度高出4.2开氏度时才能变成液态。即使在常压下进一步冷却，氦也不会形成固体，而是会产生一种量子层面上的转变，一些原子发生凝聚。

假设液态氦的温度持续降低直到绝对零度，按我们的预期，氦最终会变成固体，但根据不确定性原理，事实上它会一直保持液态。在低温条件下，原子的波函数发生重叠，每个原子的位置不确定性较低，动量不确定性较大，这些能量构成了氦原子的部分基态能量（被称为“零点能”）。原子的质量越小，零点能就越大，对于氦原子而言，即使在绝对零度，这部分能量也足以阻止原子结合成晶状固体。氢的质量比氦更小，但由于氢分子间较强的静电力，氢在高于绝对零度14开氏度时变成固体。对于更重的元素来说，每个原子动量上的不确定性并不足以使其克服在低温时变成固体的趋势。尽管氦在常压下不会以固态形式存在，然而随着一些氦原子在基态下凝聚，它会在高于绝对零度2.18开氏度时经历一次“相变”。

部分原子已经凝聚成同一个量子态的流体具有怎样的性质呢？其中一个奇妙的特性是，流体没有黏度！黏度表示所有普通流体内部的摩擦力大小，你可以将其理解为流体运动的阻力。水的黏度很小，而糖浆和电机润滑油的黏度则大得多。没有黏度的流体一旦开始运动，将持续地以恒定速度流经软管而不需要额外施加外力。这样的流体被称为“超流体”，因为它与普通流体的行为类似，却拥有量子力学的力量！[2]

1965年，实验人员在高于绝对零度4开氏度的条件下，让一个盛有液态氦的圆筒围绕着一个穿过其中心的轴旋转。这个圆筒内还装有金属屑，因此液体必须穿过金属屑之间的小孔和缝隙。液态氦在这种温度条件下还不是一种超流体，它开始随着容器旋转。于是，它的温度被降至2.17开氏度，在此温度条件下，一些氦原子会凝聚成超流体。当容器的旋转停止时，超流体仍以原来的速度继续运动。如果你停止搅拌杯子里的咖啡，液体在几秒钟之后就会静止下来，但是超流体状态的氦可以在数小时之内保持原有的运动速度，直到实验人员终止实验。

如果这个系统被加热到高于绝对零度2.17开氏度以上，超流体就会变成普通的流体，并迅速停止运动。在这里，低温是关键条件。在足够低的温度条件下，较低动量的氦原子有一个较长的物质波。因此，大量氦原子的波函数之间将发生重叠，所有原子都可以通过一个量子力学波函数来描述，这些原子一起形成了一个巨大的“超原子”。要使凝聚态中的一个氦原子的运动速度减慢，就必须通过减慢多原子波函数来实现；如果原子的旋转速度并不快，就没有足够的能量去减慢多原子波函数，超流体将保持原有的运动速度。

许多金属，甚至是一些非金属材料，都有一种类似于超流体的电学性质，被称为“超导电性”。超导电线没有电阻，类似于有超流体流过的橡胶软管。任何流入软管一端的无黏度流体都会以相同的速度从软管的另一端流出，不管软管的长度或堵塞程度如何，哪怕它环绕赤道！尽管我们不知道超导线圈中的电流是否会永远流动，但实验已经证实，10年后，一个闭合回路的超导体中的电流相比初始数值，只减少了不到1014分之一。

在普通的电导体中，外部施加的电压会产生电流。导体的电阻越小，给定电压所能产生的电流越大。在水流与电流的类比中，水压的作用与电压相似。压力越大，水受到的推力也越大。从水龙头流入橡胶软管的水流与电流类似，如果水管沿长度方向有阻塞，就会增加水流动的难度，这与电线中的电阻类似。水在与水管中的局部阻塞以及管壁的碰撞过程中会损失能量，因此需要持续施加压力才能使水流持续地从软管的另一端流出。类似地，由于电流与电线中的缺陷发生碰撞，电流也会损失部分能量。这就是为什么恒定的推力（即电压）会产生恒定的流动（即电流），而不是加速的流动（根据牛顿第二定律，力=质量×加速度，这意味着如果力是恒定的，那么加速度也应该是恒定的）。超导体没有电阻，即使不施加电压，电流也会保持不变，就像超流体状态的氦原子能够持续保持原有的运动速度。(www.chuimin.cn)

金属中的电流是由电子而非氦原子形成的。你应该还记得，电子是内禀角动量值为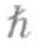/2的费米子。为了形成玻色—爱因斯坦凝聚态，两个电子必须配对组成复合粒子，其中一个电子的内禀角动量值为+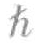/2，另一个电子的内禀角动量值为-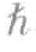/2。因此，复合粒子的总内禀角动量值为零，因而是玻色子。如此一来，在足够低的温度条件下，这些成对电子会形成凝聚态，并且没有阻力地流动。

电子带有负电荷，负电荷之间会互相排斥，可是为什么两个电子能结合在一起形成一个玻色子？答案是：带正电荷的原子，我们称之为“离子”。我们在上一章讨论过，在诸如铅之类的金属中，每个原子的最后几个未配对的电子都处于动量态。当电子处于动量态时，它能够在固体中自由移动。金属原子最初是电中性的，如果一个电子离开它所属的原子，就会留下一个带正电荷的离子（“离子”是指由于得到或失去电子而带有净电荷的原子）。这些金属离子有规律地排布在一起，构成了晶体。由于带负电荷的电子在金属中自由移动，带正电荷的离子会被它们吸引。阳离子因为太大而无法离开它们在晶体中的固有位置，但在静电吸引力的作用下，它会捕获带负电荷的电子。

随着电子的自由移动，它会将附近带正电荷的离子拉向它的运行轨迹，这与《X战警》漫画书中“万磁王”（能够掌控磁力的变种人大师）使用他的变种人能力时，金属物体向着他弯曲的情况类似。随着时间的推移，离子之间会相互排斥，并回到它们在晶体结构中的原有位置。当温度低于7开氏度时，铅离子移动缓慢，在吸引了第一个电子之后，它的带正电的路径还能够维持足够长的时间，从而使第二个电子也被吸引过来。通过这种方式，两个带负电荷的电子结合在一起形成所谓的“库珀对”（以莱昂·库珀的名字命名，他率先从理论上证明了，在低温状态下，这种结合机制在金属中是可行的）。当两个电子处于最低能量态时，它们的内禀角动量值分别为+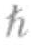/2和-/2，因此由这两个电子组成的“库珀对”的内禀角动量值为零，我们可以将其视作一个玻色子。

当金属中的部分电子形成库珀对，并且凝聚到一个低能态时，我们就会观测到超导现象。当许多库珀对的波函数发生重叠时，它们就会形成一个多粒子波函数。在普通金属中，电流与振荡的原子或者金属中的缺陷发生碰撞会损失能量，这就是为什么需要一个恒定的电压来使电流保持稳定。要想减慢由波函数重叠的库珀对凝聚形成的超级电流的速度，就必须通过碰撞把库珀对拆开，并改变所有波函数重叠的库珀对的能量。但在温度较低或电流较缓和的情况下，这是不可能实现的。库珀对能够负载电流（假设电流不太强）且没有任何损失，就像超流体中的氦原子能够一直保持原来的运动状态一样。

在金属中有许多可以自由移动的电子，但并不需要所有电子都结成库珀对才能让金属显示出超导性质。那么，那些没有结成库珀对的电子在做什么呢？电阻对它们仍然起作用，但由于超级电流的存在，这部分电子将不再参与电流的传输。举个例子，我有两条路可以到达目的地，其中一条是崎岖不平、坑坑洼洼的土路，限速每小时8.054千米；另一条是没有最高时速限制的高速公路，毫无疑问我会选择第二条路。一旦金属被冷却到可以形成库珀对的低温，金属中的所有电流将全部由具有超导性的库珀对来传输。类似地，在超流体中，并不是所有的氦原子都处于凝聚态。只要超导体或者超流体中的部分粒子处于能量较低的凝聚态，它们就会表现出协同行为。

超导体不仅可以不受阻碍地传输电流，它们也是完美的抗磁性物质，这意味着它们会排斥任何外部磁场。一些金属会被磁体吸引，一些实际则不会，金和银就属于后一类金属。如果你能用冰箱贴把你的金首饰吸住，那么你应该考虑退货。金原子的内部磁场的极化方向与外部磁场相反，因此它们会形成一个北极，正对着外部磁场的北极。因为北极和北极相斥，所以磁体对金不起作用；或者，如果外部磁场足够强，金就会因为它所具有的抗磁性而被磁体推开。

之所以说超导体是完美的抗磁性物质，是因为它们产生的电流在固体内部形成磁场，恰好抵消了外部磁场的影响。超导体没有电阻，一旦电流产生，只要施加外部磁场，电流就可以持续不断地使得超导体成为建造磁悬浮列车轨道的理想材料。目前，超导材料的缺陷在于，大多数金属只在超低温条件下才具有超导电性。在第六部分，我们会介绍被称为“高温超导体”的材料，这些材料在较高的温度条件（尽管还达不到室温）下就可以显示出超导电性，它们甚至不是金属。

除了在粒子加速器或者大量宇宙射线中产生的某些基本粒子之外，大多数有质量的玻色子都是复合粒子，比如氦原子核或者库珀对。然而，有一种很常见的无质量粒子，它的内禀角动量值为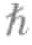，并符合玻色—爱因斯坦统计规则，这种粒子就是光！

我们在第1章中提到，马克斯·普朗克对发热物体的发光光谱的解释（见图2-1），开启了量子时代。对物体的发光强度进行测量的结果，可用光的频率函数来表示。我们会发现，在低频和高频区域仅有很少的光，而且光强峰值对应的频率只取决于物体的温度（图2-1可表示现在你身边任意一个物体的发光光谱）。在普朗克之前的理论物理学的计算结果表明，在低频区域光强的确很小，但会随着频率的增加而无限增大。我们现在已经掌握了足够多的量子统计数据，让我们来看看这些理论物理学家到底错在哪里。

一盒分子，比如气体，会有一定的总能量，能量的大小取决于它的温度。非量子热力学的一个核心原则是，当气体分子互相碰撞时，会传递它们的能量，因此在平衡状态下，每个分子的能量相同，都是气体总能量的一部分。因为存在随机的波动，所以我们可能会发现能量略多或略少于平均能量的分子。但随后与其他分子的碰撞，会使该分子的能量回归平均能量。将盒子中数万亿兆个分子的平均能量加在一起，你会得到气体的总能量。这不仅非常合理，也是在真实的气体中观察到的情形（当分子的量子属性可以忽略时，即在高温低压条件下，分子的物质波不会发生重叠）。

如果盒子中充满光线，并被当作延展的电磁波来处理，情况又会如何呢？盒子中处于某一温度的原子在它们正常的位置附近来回振动。在量子力学出现之前，人们就已经知道振荡的电子会发出电磁波，这是无线电收音机和电视的工作原理。如果盒子中有一些灰尘能够吸收并发射光线，起到与上文描述的气体分子间的相互碰撞相同的作用，那么每个波都将具有相同的能量。

在1900年马克斯·普朗克的论文发表之前，非量子热力学是热力学的唯一存在形式。这种热力学理论认为，每个波的能量等于系统温度乘以一个常数。对于充满气体分子的盒子来说，这一方法非常适用。在这种情况下，将数万亿兆个分子的能量相加，就能得到气体的总能量。一万亿兆是一个很大的数字，但也只是一个数字。然而，盒子中的波的频率是没有上限的。在弹奏两端固定的吉他弦时，会存在一个可能的最低频率，但是原则上，最高频率却没有上限。如果每个可能的波都有相同的能量，并且有无限多可能的波，那么盒子中光的总能量也是无限的！幸运的是，真实物体并非这样，否则，所有物质都将以X射线或伽马射线的形式释放出无限多的能量。这是毁灭性的，所以物理学家称其为“紫外灾难”。

为了解决光强度谱图在计算和观测上的矛盾，普朗克假定盒子中的原子只能以与光的频率成比例的步幅损失能量，从而提出了能量=h×频率这一关系式。经过百余年的不断探索，量子力学已经取得了长足发展。与普朗克在1900年提出的理论相比，我们可以用更简单的方法来解释实验中观测到的所有物体的发光光谱。

装满光的盒子可以被看作一种光子气体，其中每一个光子的内禀角动量值都是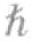。因此，这些光子都是玻色子，它们遵循玻色—爱因斯坦统计原则。对于气相的玻色子，粒子处于较低能量态的概率更高。大多数玻色子都处于最低能量态，少数玻色子处于较高能量态，个别玻色子会处于很高能量态，最高能量态被占据的概率则很小。

光子气体的能量是光的频率函数，它等于光子的能量（E=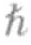×f）乘以处于该能量态的光子数目。大部分光子都处于低能量态，高能量态被占据的概率很小，因此高能态的光子对平均能量的贡献也很小。单个光子的能量越大，处于该能量态的光子数目越少。将单个光子的能量与处于该能量态的光子数目相乘，可以得到每个频段的平均能量。这一能量在低频区很小，在中频区达到峰值，在高频区又变得很小，与实验观测结果完全相符。

这有点儿类似“强力球”或乐透彩票的奖金。为了赢得大奖，彩票玩家必须猜对全部6个数字。即使没有人猜对全部6个数字，猜对其中几个数字的情况也是有可能发生的。只猜对3个数字的人会得到一笔数额较小的奖金，比如10美元。猜对4个数字的人可能会赢得一万美元，猜对5个数字的人可能会赢得10万美元。奖金额度起初很小，许多玩家可能只猜对了一两个数字，他们颗粒无收；有些玩家猜对3个数字，但他们赢得的奖金数额很小；猜对4个数字的玩家更少，他们会赢得一笔不少的钱；很少有人能猜对5个数字，所以他们赢得的奖金占比比较小（巨额的奖金池，但是获奖者很少）。根据彩票机构发放的总奖金额与奖金的级别作图，我们会发现奖金额在一开始时很小，逐渐到达某一峰值，随后又开始减少。

当我们设定了容器大小后，盒子中气体分子的数目便是固定的，但光子数目却可以随着温度而改变。热的物体会发出很亮的光（也就是放射出大量的光子），冷的物体则放射出较少数目的光子。在高温状态下，表示光子数量的指数型曲线的尾部会延伸至更高能量区域。发光体的发光光谱峰值与频率有关，因此取决于这个物体的温度：冷的物体的峰值出现在频率较低的位置，物体的温度越高，曲线的峰值就越大。

因此，我们可以根据测量到的可被视为“黑体”的物体光谱，来确定非常热的物体的温度，比如鼓风炉的内部或者太阳表面的温度。当然，这项技术也适用于冷的物体。宇宙空间中充满微波辐射，这种辐射是来自“创世大爆炸”的残余能量，其光谱可以表示为频率函数。通过对该光谱进行测量，我们发现，如果宇宙的特征温度为2.7开氏度，则完全符合普朗克表达式。第2章的图2-1实际上显示的是测量宇宙微波辐射的黑体光谱，这种辐射遍布宇宙，此时此刻也遍布在你这名“无畏”的读者周围！根据测量到的宇宙膨胀速率，我们可以推算出宇宙大约花了150亿年的时间才冷却到现在的温度。量子力学是为了解释原子与光相互作用的方式而发展起来的，它告诉我们可以利用放射性同位素的衰变规律来确定地球的年龄。现在我们知道，量子物理学也向我们揭示了宇宙中最古老事物的年龄——宇宙的年龄！

[1]如第12章所讨论的，函数A和B是单粒子波函数的乘积，A=Ψm（1）Ψn（2），B=Ψn（1）Ψm（2），其中Ψm（1）表示一个在位置1处于量子态m的玻色子的波函数；而Ψn（2）代表一个在位置2处于量子态n的玻色子的波函数。如果粒子1和2的位置互换，那么总波函数甲=A+B=Ψm（1）Ψn（2）+ Ψn（1）Ψm（2）保持不变。

[2]氦变成超流体时发生的变化，或者电子在超导体中形成“库珀对”，并不属于严格意义上的玻色—爱因斯坦凝聚态。真正的玻色—爱因斯坦凝聚态与超流体或超导态的区别是一个很专业的问题，为了便于理解，我们在这里可以将它们等同起来。