续表考点:导数在研究函数中的应用(2017全国I,21)已知函数f(x)=ae2x+(a-2)ex-x.(1)讨论f(x)的单调性;(2)若f(x)有两个零点,求a的取值范围.1.(2017山东莱芜二模)已知函数f(x)=ex[x2+(a+1)x+2a-1].(1)当a=-1时,求函数f(x)的单调区间;(2)若关于x的不等式f(x)≤ea在[a,+∞)上有解,求实数a的取值范围;(3)若曲线y=......
2025-09-30
【主要内容】
1.二元函数极限与连续的概念
设二元函数f(x,y)在点(x0,y0)的某个去心邻域{(x,y)|0<(x-x0)2+(y-y0)2<δ2}(其中,δ是某正数)内有定义.如果动点(x,y)以任何方式无限趋于点(x0,y0)时,f(x,y)总是无限趋于常数A,则称A是点(x,y)趋于点(x0,y0)(记为(x,y)→(x0,y0))时f(x,y)的极限,记为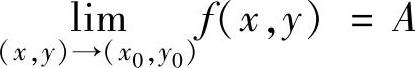 或
或
注 根据定义,可以按以下方法判定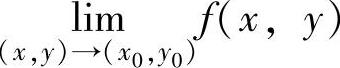 是否存在:
是否存在:
(ⅰ)如果点(x,y)按某种方式趋于点(x0,y0)时,f(x,y)不趋于任一值,则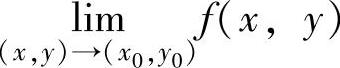 不存在;
不存在;
(ⅱ)如果点(x,y)按某两种方式趋于点(x0,y0)时,f(x,y)趋于两个不同值,则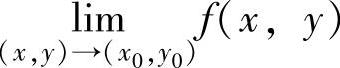 不存在.
不存在.
设二元函数f(x,y)在点(x0,y0)的某个邻域内有定义.如果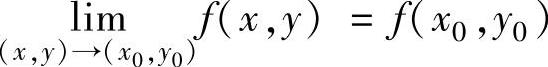 ,则称f(x,y)在点(x0,y0)处连续.
,则称f(x,y)在点(x0,y0)处连续.
如果f(x,y)在区域D的每一点处都连续,则称f(x,y)在区域D上连续.
注 当f(x,y)是有界闭区域D上的连续函数时,它有以下性质:
(ⅰ)f(x,y)在D上必有最大值和最小值,即在D上存在点(x0,y0)和(x1,y1),使得
f(x0,y0)=M(f(x,y)在D上的最大值),f(x1,y1)=m(f(x,y)在D上的最小值)
(ⅱ)f(x,y)可以取到其在D上的最小值m和最大值M之间的任何值C,即存在(ξ,η)∈D,使得f(ξ,η)=C.
2.二元函数偏导数的定义与计算
设二元函数f(x,y)在点(x0,y0)的某个邻域内有定义.如果极限
存在,则称这个极限值为f(x,y)对x(或y)的偏导数,记为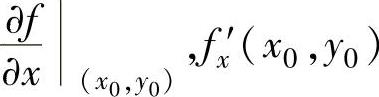 (或
(或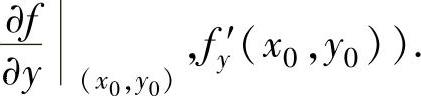
根据定义,fx′(x0,y0)与fy′(x0,y0)可分别通过计算函数f(x,y0)在点x0处的导数与函数f(x0,y)在点y0处的导数得到.
注 当(x,y)是区域D上的任一点时,f(x,y)在该点对x(或对y)的偏导数为fx′(x,y)简记fx′,或 称为偏导函数(简称偏导数),它们往往是关于x,y的二元函数.
称为偏导函数(简称偏导数),它们往往是关于x,y的二元函数.
3.二元函数二阶偏导数的定义与计算
设二元函数f(x,y)的偏导函数fx′(x,y),fy′(x,y)在点(x0,y0)仍有偏导数,则称这些偏导数为f(x,y)在点(x0,y0)的二阶偏导数,记为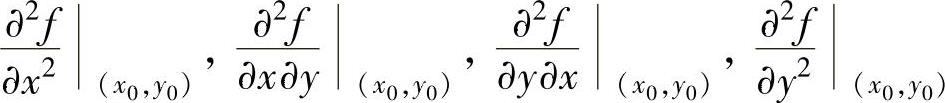 ,或对应地记为fx″x(x0,y0),fx″y(x0,y0),fy″x(x0,y0),fy″y(x0,y0).
,或对应地记为fx″x(x0,y0),fx″y(x0,y0),fy″x(x0,y0),fy″y(x0,y0).
根据定义,fx″x(x0,y0)可以通过计算f(x,y0)在点x0处的二阶导数得到,fy″y(x0,y0)可以通过计算f(x0,y)在点y0处的二阶导数得到,而fx″y(x0,y0)可以通过计算fx′(x0,y)在点y0处的导数得到,fy″x(x0,y0)可以通过计算fy′(x,y0)在点x0处的导数得到.
如果函数f(x,y)在区域D的任一点(x,y)处都有二阶偏导数,则记为
或相应地记为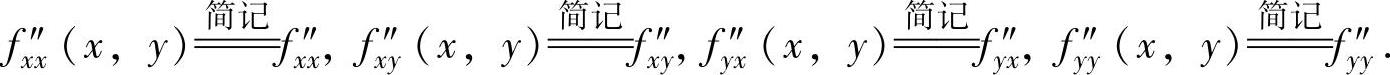
显然,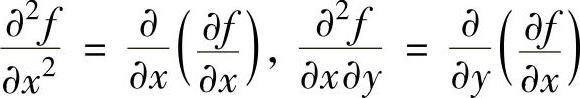 ,
, ,
,
注 (ⅰ)设函数f(x,y)的两个二阶混合偏导数fx″y,fy″x在点(x0,y0)处(在区域D)连续,则在点(x0,y0)(在区域D)有fx″y=fy″x.
(ⅱ)f(x,y)的三阶、四阶偏导数也可用类似方法定义.(https://www.chuimin.cn)
【典型例题】
例3.1.1 设二元函数 求fx′(0,0)和fx″y(0,0).
求fx′(0,0)和fx″y(0,0).
精解 先由偏导数定义计算出fx′(0,0)和fx′(0,y)(y≠0),然后再由偏导数定义计算fx″y(0,0).
此外,由于y≠0时,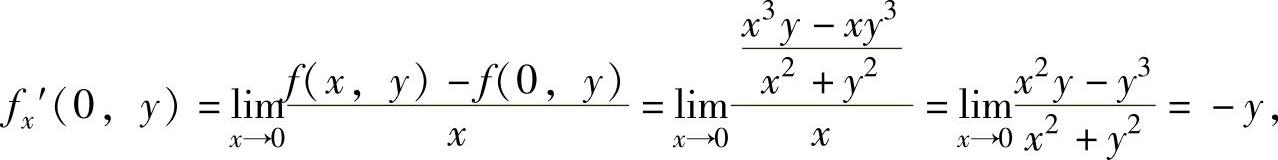
所以,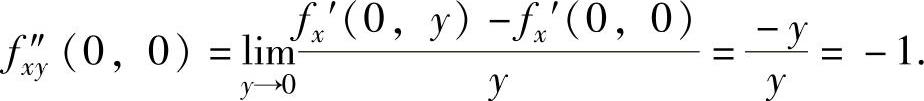
例3.1.2 设二元函数
(1)求fx′(0,0),fy′(0,0);
(2)讨论fx′(x,y)在点(0,0)处的连续性.
精解 (1)按定义计算fx′(0,0)和fy′(0,0).
(2)当x2+y2≠0时,
所以,
由于, ,即
,即 不存在,所以fx′(x,y)在点(0,0)处不连续.
不存在,所以fx′(x,y)在点(0,0)处不连续.
例3.1.3 设z=yx+xy.求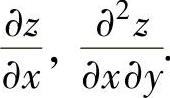
精解 先分别计算z1=yx,z2=xy的一阶和二阶偏导数:
所以, ,
,
例3.1.4 设二元函数f(x,y)满足 ,求f(x,y)的表达式.
,求f(x,y)的表达式.
精解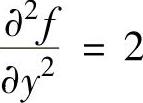 的两边对y积分(此时将x看做常数)得
的两边对y积分(此时将x看做常数)得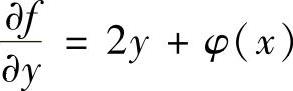 (其中,φ(x)是关于x的待定函数).(1)
(其中,φ(x)是关于x的待定函数).(1)
在式(1)中,令y=0,则由题设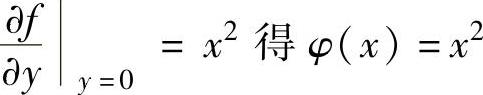 ,将它代入式(1)得
,将它代入式(1)得
上式两边对y积分(此时将x看做常数)得
f(x,y)=y2+x2y+ψ(x)(其中,ψ(x)是关于x的待定函数).(2)在式(2)中令y=0,则由题设f(x,0)=x得ψ(x)=x.将它代入式(2)得
f(x,y)=y2+x2y+x.
注 对一元函数f(y)来说,由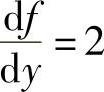 得f(y)=2y+C(其中,C是任意常数),但对二元
得f(y)=2y+C(其中,C是任意常数),但对二元
函数f(x,y)来说,由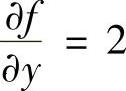 得f(x,y)=2y+φ(x)(其中,φ(x)是关于x的任意函数).
得f(x,y)=2y+φ(x)(其中,φ(x)是关于x的任意函数).
相关文章

续表考点:导数在研究函数中的应用(2017全国I,21)已知函数f(x)=ae2x+(a-2)ex-x.(1)讨论f(x)的单调性;(2)若f(x)有两个零点,求a的取值范围.1.(2017山东莱芜二模)已知函数f(x)=ex[x2+(a+1)x+2a-1].(1)当a=-1时,求函数f(x)的单调区间;(2)若关于x的不等式f(x)≤ea在[a,+∞)上有解,求实数a的取值范围;(3)若曲线y=......
2025-09-30

【主要内容】1.设函数f(x)在点x0的某个去心邻域内有定义,则limx的充分必要条件是注 (ⅰ)对任意ε>0,如果存在δ>0,当0<|x-x0|<δ时有|f(x)-A|<ε.对任意ε>0,存在δ>0,使得-δ
2025-09-30

知识要点一、函数的概念1.函数、反函数、基本初等函数、初等函数、复合函数的定义.2.理解函数记号y=f(x)中“f”的意义.函数的两个要素,对于两个或两个以上的函数,只有定义域和对应法则完全相同时才是同一函数.3.弄清基本初等函数的概念,熟悉这些函数的特性.4.求f(x)的定义域.对于较复杂的函数求定义域问题,就是求解由简单函数的定义域所构成的不等式组的解集.5.函数的重要性质:有界性,奇偶性,周......
2025-09-30

【主要内容】1.函数在点x0处可导与导数的定义设函数f(x)在点x0的某个邻域内有定义.如果极限存在,则称f(x)在点x0处可导,且称这个极限的值为f(x)在点x0处的导数,记为f′(x0)或注 函数在点x0处可导,必在点x0处连续,但反之未必正确.函数f(x)在点x0处可导的充分必要条件是f(x)在点x0处的左导数f-′(x0)和右导数都存在且相等.注 当x0是分段函数的分段点时,要判定f(x)......
2025-09-30

1.设函数f在[a,b]上连续,则f在[a,b]上必有最大值M与最小值m.它们可按以下步骤计算:算出f在(a,b)内的所有可能极值点,记为x1,x2,…......
2025-09-30

轧机作业线上带钢纵向高速运行时,带钢的中心线或带钢的边缘会向两侧偏移,这种现象称为跑偏。带钢跑偏必须限制在一定的公差范围内,否则就会刮坏设备或使得带材边缘损坏,影响成品质量,跑偏严重时还会导致不能正常生产,所以带钢跑偏控制是带材连续作业线上必不可少的环节。4)光电液伺服系统:采用光电检测器将跑偏信号检测出来并经过放大器放大,控制电液伺服阀推动液压缸进行纠偏。......
2025-09-29
相关推荐