首页理论教育泰勒公式及应用数学基础篇

泰勒公式及应用数学基础篇

2023-10-27 理论教育版权反馈

【摘要】：【主要内容】1.带拉格朗日型余项的泰勒公式设函数f（x）在[a，b]上具有直到n阶的连续导数，在（a，b）内具有n+1阶导数，则对x0∈[a，b]，有（x∈[a，b]）.（1）其中，余项，ξ是介于x0与x之间的实数）.设函数f（x）在（a，b）上具有直到n+1阶导数，则对x0∈（a，b），有其中，余项，ξ是介于x0与x之间的实数）.式（1）和式（2）称为f（x）按（x-x0）的幂展开的带拉格朗日型

【主要内容】

1.带拉格朗日型余项的泰勒公式

设函数f（x）在[a，b]上具有直到n阶的连续导数，在（a，b）内具有n+1阶导数，则对x₀∈[a，b]，有

（x∈[a，b]）.（1）

其中，余项，ξ是介于x₀与x之间的实数）.

设函数f（x）在（a，b）上具有直到n+1阶导数，则对x₀∈（a，b），有

其中，余项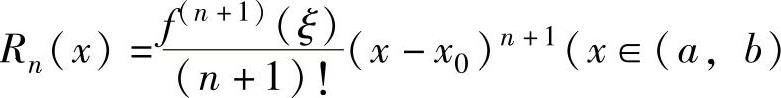，ξ是介于x₀与x之间的实数）.

式（1）和式（2）称为f（x）按（x-x₀）的幂展开的带拉格朗日型余项的n阶泰勒公式.当x₀=0时，式（1）和式（2）称为f（x）的带拉格朗日型余项的n阶麦克劳林公式.

（1）常用函数的带拉格朗日型余项的麦克劳林公式，，，，

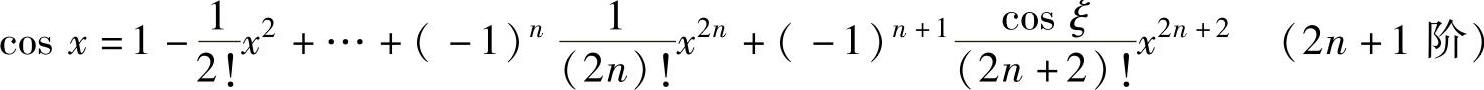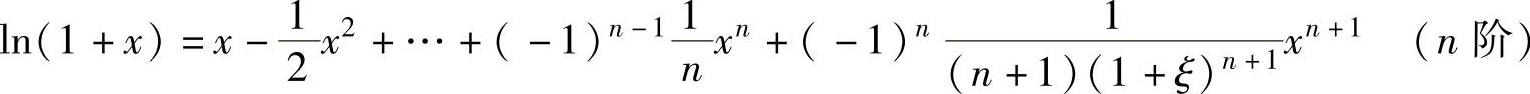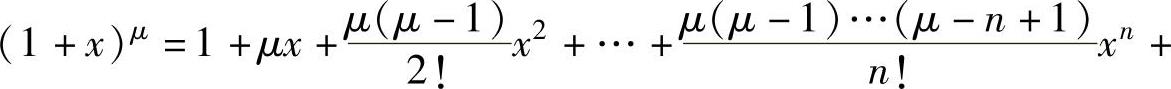
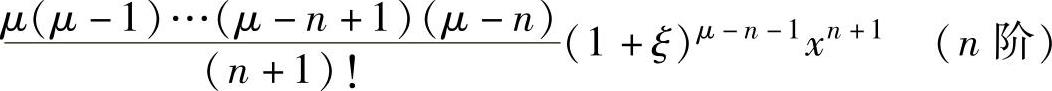
其中，以上各式的ξ是介于0与x之间的实数.

（2）带拉格朗日型余项的泰勒公式常应用于证明：对于二阶或三阶可导的函数f（x），存在ξ，使得关于f″（ξ）=k（k为常数）或f‴（ξ）的表达式成立.

2.带佩亚诺型余项的泰勒公式

设函数f（x）在点x₀的某个邻域内有直到n阶导数，则对这个邻域内的x，有

（3）

式（3）称为f（x）按（x-x₀）的幂展开的带佩亚诺型余项的n阶泰勒公式.当x₀=0时，式（3）称为f（x）的带佩亚诺型余项的n阶麦克劳林公式.

（1）常用函数的带佩亚诺型余项的麦克劳林公式，，，，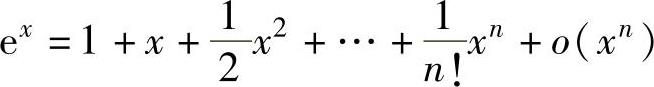

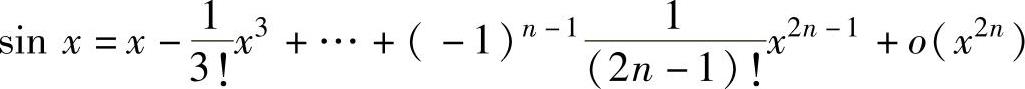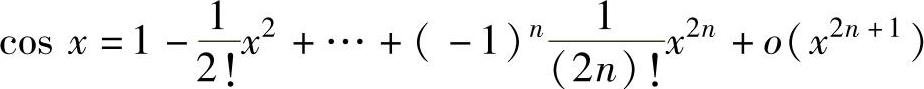（2）带佩亚诺型余项的泰勒公式常用于寻找比较复杂的函数在x→x₀时的等价无穷小或计算函数在点x₀处的高阶导数的情形.

【典型例题】

例1.15.1 计算下列各题：

（1）求函数f₁（x）=e^xsinx的带拉格朗日型余项的四阶麦克劳林公式；

（2）求函数f₂（x）=lnx的按（x-2）的幂展开的带拉格朗日型余项的四阶泰勒公式.

精解分别计算f₁（x）和f₂（x）的直到五阶导函数，即可得到要求的公式.(www.chuimin.cn)

（1）f₁（x）=e^xsinx，，，

同理可得，，

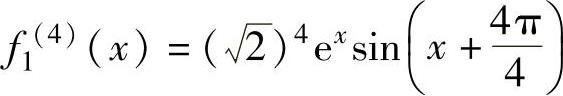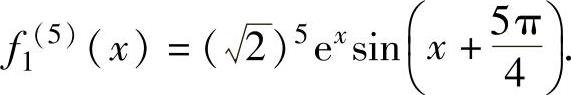
所以，f₁（x）的带拉格朗日型余项的四阶麦克劳林公式为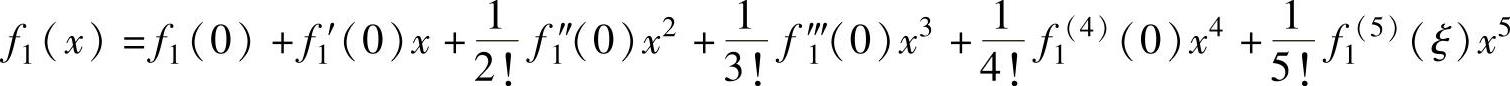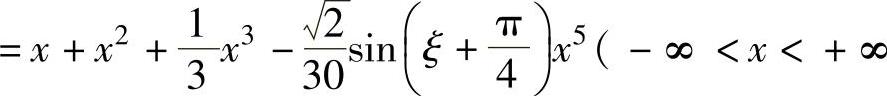，ξ是介于0与x之间的实数）.

（2）由于f₂（x）=lnx，，，，，，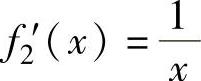

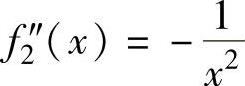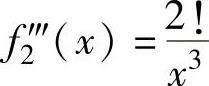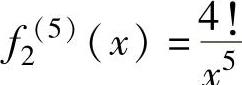所以，f₂（x）的按（x-2）的幂展开的带拉格朗日型余项的四阶泰勒公式为

（0<x<+∞，ξ是介于2与x之间的实数）.

例1.15.2 试确定常数A，B，C的值，使得x→0时，e^x（1+Bx+Cx²）=1+Ax+o（x³）.

精解只要写出e^x（1+Bx+Cx²）的带佩亚诺型余项的三阶麦克劳林公式即可.

由于，

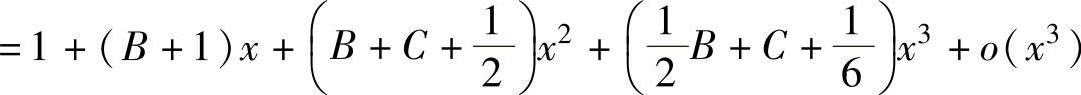将它代入e^x（1+Bx+Cx²）=1+Ax+o（x³）中并比较x的同次幂系数得

解此方程组得，，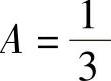

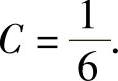
例1.15.3 求极限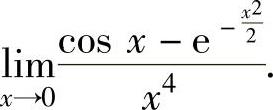

精解先写出cosx-e-^x2²的带佩亚诺型余项的四阶麦克劳林公式（因为函数的分母是x⁴，所以分子只需写出4阶麦克劳林公式即可），寻找等价无穷小，然后应用等价无穷小代替定理计算所给的极限.由于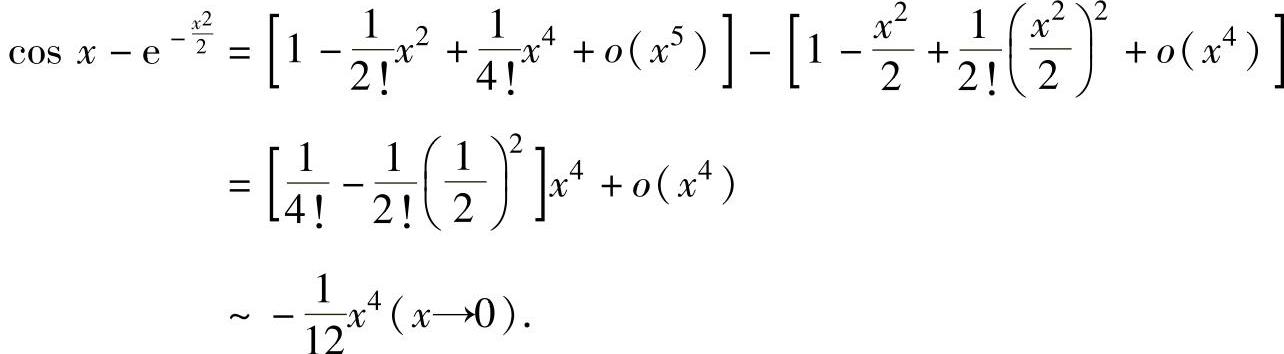

所以，由等价无穷小代替定理知

例1.15.4 设函数f（x）在包含原点的某个区间（a，b）内二阶可导，且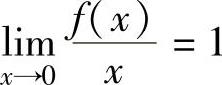，f″（x）>0（a<x<b）.证明：f（x）≥x（a<x<b）.

精解由于f（x）二阶可导，所以对于x∈（a，b），f（x）有带拉格朗日型余项的一阶麦克

劳林公式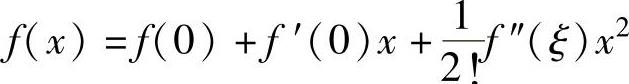（ξ是介于0与x之间的实数）.（1）

由题设及f（x）在点x=0处连续可得，f（0）=0，f′（0）=1.将它们代入式

（1）并利用f″（x）>0（a<x<b）得

注当函数f（x）在点x₀连续，且满足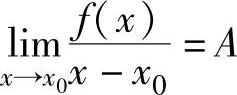时，有f（x₀）=0，f′（x₀）=A.应记

住这个结论.