高等数学作业-奇偶性与复合过程

班级_______________　姓名_______________　学号_______________

高等数学作业1　函数

一、选择题

二、填空题

三、计算题

3.判断下列函数的奇偶性.

4.指出下列函数的复合过程.

5.已知y=lnu，u=x3+1，把y表示成x的函数.

6.已知s=u2，u=1+，v=sint，把s表示成t的函数.

班级_______________　姓名_______________　学号_______________

高等数学作业2　极限的概念

一、选择题

二、填空题

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

四、计算题

1.设函数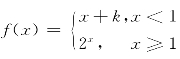，当x→1时的极限为2，求k的值.

2.设函数，讨论当x→-1，x→0和x→1时的极限.

班级_______________　姓名_______________　学号_______________

高等数学作业3　极限的运算

一、填空题

二、选择题

1.下列正题的是（　）.

2.下列各极限中正确的是（　）.

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

四、计算题

1.求下列极限.

2.已知极限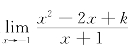存在，求k的值，并求这个极限.

班级_______________　姓名_______________　学号_______________

高等数学作业4　无穷小与无穷大

一、填空题

二、选择题

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

四、利用等价无穷小代换，求下列函数的极限

班级_______________　姓名_______________　学号_______________

高等数学作业5　函数的连续

一、填空题

二、选择题

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

1.f（x）在x0处有定义是f（x）在x0连续的必要条件.　（　）

2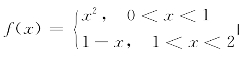的连续区间是（0，2）.　（　）

四、讨论及证明题

1.讨论函数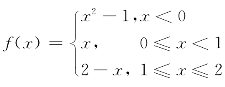，在点x=0和x=1处连续性.

2.证明方程x4-4x+2=0在区间（1，2）内至少有一个根.

3.证明方程x2x-1=0至少有一个小于1的正根.

班级_______________　姓名_______________　学号_______________

高等数学作业6　导数的概念

一、选择题

二、填空题

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

1.函数f（x）在x=x0处可导必定在x=x0处连续.　（　）

2.y=|x-1|在x=1处连续、可导.　（　）

3.函数y=f（x）在x0点的导数等于［f（x0）］′.　（　）

4.若曲线y=f（x）在（x0，f（x0））点处有切线，则曲线y=f（x）在x0一定有导数.（　）

5.设函数y=f（x）=xx，则y′=x·xx-1.　（　）

四、计算及证明题

1.证明函数在x=0处连续并可导.

班级_______________　姓名_______________　学号_______________

高等数学作业7　函数的微分法

一、选择题

二、填空题

1.曲线y=x3+2x+1在点（0，1）处的切线方程是______________________.

2.过曲线y=x3-1上的点P（-2，-9）的切线斜率为_________.

3.设y=arctanx2，则y′=______________________.

4.设y=cos2x，则y′=______________________.

5.设f（x）=ex+1，则f′（x+1）=______________________.

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

四、计算题

1.求下列函数的导数.

（5）y=2sin2x+1（6）设y=sin3（2x+1），求y′.2.求在曲线y=上哪一点的切线与直线y=3x-1平行？

班级_______________　姓名_______________　学号_______________

高等数学作业8　函数的微分及其应用

一、选择题

二、填空题

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

四、计算题

求下列函数的微分.

班级_______________　姓名_______________　学号_______________

高等数学作业9　隐函数及由参数方程所确定的函数的微分法

一、选择题

二、填空题

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

四、计算题

1.求下列隐函数的导数.

2.求下列由参数方程所确定的函数的导数.

3.设函数y=f（x）由方程exy+x-y+1=0确定，求.

4.设y=f（x）由参数方程所确定，求.

5.设，求y′.

6.已知y=xsinx（x＞0），求y′.

班级_______________　姓名_______________　学号_______________

高等数学作业10　高阶导数

一、填空题

1.设f（x）=ln（1-2x），则f″（0）=_________.

2.设y=ax，则y（n）=_________.

3.物体作直线运动的方程为S=-10t2+3t+150，则当t=1时的速度为________，加速度为_________.

4.设y=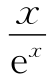，则y″=_________.

二、选择题

1.设y=cos22x，则y″=（　）.

A.4cos2x　B.-8sin2x　C.8cos2x　D.-8cos2x

2.设y=f（-2x），则y″=（　）.

A.2f″（-2x）　B.4f″（-2x）　C.-2f″（-2x）D.-4f″（-2x）

3.设y=cosx，则y（10）=（　）.

A.sinx　B.-cosx　C.-sinx　D.-cosx

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

1.设y″=x3-4x2+6x-2，则y‴（0）=6.　（　）

四、计算题

1.y=x3e2x，求y″.

2.设y=arctan2x，求y″（1）.

3.设y=xex，求y（n）.

班级_______________　姓名_______________　学号_______________

高等数学作业11　微分中值定理　罗必达法则

一、选择题

1.在区间［-1，1］上满足罗尔定理条件的函数是（　）.

2.下列给定的相限都存在，不能使用洛必达法则的是（　）.

3.方程5x4-4x+1=0在0与1之间至少有（　）实根？

A.2　B.3　C.1　D.4

二、填空题

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

四、计算题

班级_______________　姓名_______________　学号_______________

高等数学作业12　函数的单调性及极值

一、选择题

1.若x0为f（x）的极值点，则下列命题正确的是（　）.

A.f′（x0）=0　B.f′（x0）≠0

C.f′（x0）=0或f′（x0）不存在　D.f′（x0）不存在

2.f′（x）＜0，x∈（a，b）是函数y=f（x）在区间（a，b）内单调减少的（　）.

A.必要条件　B.充分条件　C.充要条件　D.无关条件

3.函数y=x-arctanx在（-∞，+∞）内（　）.

A.单调增加　B.单调减少　C.单调　D.无法判定

4.下列命题正确的是（　）.

A.x0是f（x）的极值点，且f′（x0）存在，必有f′（x0）=0

B.x0是f（x）的极值点，则x0必为f（x）的驻点

C.若f′（x0）=0，则x0必为f（x）的极值点

D.f（x）在（a，b）内的极大值必大于极小值

5.下列命题正确的是（　）.

A.函数f（x）在（a，b）内单调递减且在（a，b）内可导，则必有f′（x）＞0

B.函数f（x）在（a，b）内的极大值必大于极小值

C.函数f（x）在［a，b］内连续，f（a）=f（b），则一定有ξ∈（a，b）使f′（ξ）=0

D.函数的极值点不一定是驻点

二、填空题

1.f′（x0）=0是可导函数f（x）在x=x0处取极值的________条件.

2.f′（x）＞0，x∈（a，b）是可导函数y=f（x）在（a，b）内单调递增的_________条件.

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

1.x=0是f（x）=|x|x2的极小值点.　（　）

2.f（x0）=0，f″（x0）＞0，则函数f（x）有极小值.　（　）

3.y=1-x3在（-∞，+∞）内无极值.　（　）

4.y=3x3-4x在区间上单调增加.　（　）

四、计算题

1.求y=sinx+cosx在［0，π］上的极值.

2.求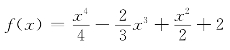的单调区间及极值.

3.设f（x）=x3+ax2+bx在x=1处有极值f（1）=2，求a、b之值.

4.设处取得极值，求a的值，并判断它是极大值还是极小值，并求此极值.

班级_______________　姓名_______________　学号_______________

高等数学作业13　函数的最大值和最小值

一、填空题

1.f（x）=x+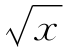在［0，4］上的最大值是________，最小值是________.

2.若连续函数f（x）在区间［a，b］内恒有f′（x）＜0，则在［a，b］上函数的最大值是________.

二、选择题

1.已知M，m分别是f（x）在区间［a，b］上的最大值及最小值，若M=m，则f′（x）=（　）.

A.0　B.1　C.M　D.m

2.y=ln（x2+2）在x=0处取得其定义域上的（　）.

A.极大值但不是最大值　B.极大值且是最大值

C.极小值但不是最小值　D.极小值且最小值

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

1.f（x）=|x|在x=0处取得最小值.　（　）

2.y=2x2+1在（-1，1）内最大值是3.　（　）

3在［-1，1］上的最小值是f（1）.　（　）

四、计算题

要造一圆柱形油罐，体积为V，问底面半径r和高h各为多少时，才能使表面积最小？这时底面直径d与h高的比是多少？

班级_______________　姓名_______________　学号_______________

高等数学作业14　不定积分的概念和性质

一、填空题

二、选择题

1.下列各式中不正确的是（　）.

2.设f（x）的原函数为，则f（x）=（　）.

3.函数f（x）在x=x0处的切线方程为y=2x-5，则f′（x0）为（　）.

A.-2　B.5　C.2　D.-5

三、计算题

班级_______________　姓名_______________　学号_______________

高等数学作业15　换元积分法（一）

一、选择题

二、计算题

班级_______________　姓名_______________　学号_______________

高等数学作业16　换元积分法（二）

计算题

班级_______________　姓名_______________　学号_______________

高等数学作业17　分部积分法

计算题

班级_______________　姓名_______________　学号_______________

高等数学作业18　定积分的概念和性质

一、填空题

二、选择题

三、证明题

班级_______________　姓名_______________　学号_______________

高等数学作业19　微积分基本公式

一、填空题

二、选择题

三、计算题

班级_______________　姓名_______________　学号_______________

高等数学作业20　定积分的换元积分法和分部积分法

一、填空题

二、计算题

三、证明题

班级_______________　姓名_______________　学号_______________

高等数学作业21　广义积分

一、填空题

二、计算题

班级_______________　姓名_______________　学号_______________

高等数学作业22　定积分在几何中的应用

计算题

1.直线y=2x，y=x与y=2所围成的图形的面积.

2.曲线y=x2与直线y=2x+3所围成的图形的面积.

3.曲线y=ex与直线y=e，x=0所围成的图形的面积.

4.曲线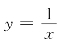与直线y=x，x=2所围成的图形的面积.

5.曲线y=x2，y=（x-2）2与x轴所围成的图形的面积.

6.曲线y2=2x与直线y=x-4所围成的图形的面积.

7.曲线y2=x与直线x-2y=3所围成的图形的面积.

班级_______________　姓名_______________　学号_______________

高等数学作业23　微分方程的基本概念及可分离变量微分方程

一、填空题

1.xdy-ydx=0的阶数是_________________________.

2.xdy=ydx-dy满足y（0）=2的特解是_________________________.

3.x2y′=（x-1）y的 通解是　_________________________.

4.x′（t）+2x（t）=0满足初始条件x（0）=3的特解是__________________________.

二、选择题

1.微分方程（　）是可分离变量方程.

2.微分方程F（x，y4，y′，（y″）2）=0时通解中含有（　）个任意常数.

A.1　B.2　C.4　D.5

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

1.（y′）2+2y=cosx是二阶微分方程.　（　）

2.xy″-5y′+3x2y=ln2x是二阶线性微分方程.　（　）

3.xdx+ydy=0的通解是x2+y2=c.　（　）

四、求下列可分离变量的微分方程的通解或在给定初始条件下的特解

1.y′=10x+y.

2.xy′-ylny=0.

5.已知一曲线过点（1，2），且该曲线上任一点P（x，y）处的切线斜率为2x+1，求该曲线方程.

班级_______________　姓名_______________　学号_______________

高等数学作业24　一阶微分方程

一、填空题

1.微分方程的通解是__________________________.

2.微分方程xy′-y=x3+x2的通解是_________________________.

3.微分方程y′+ycosx=e-sinx的通解是__________________________.

二、选择题

1.微分方程y2dx-（1-x）dy=0是（　）微分方程.

A.一阶线性齐次　B.一阶线性非齐次

C.可分离高量　D.二阶线性齐次

2.以下微分方程中，关于y的二阶线性方程是（　）.

3.y′+ay=b（a、b均为非零常数）则满足y|x=0=0的特解是（　）.

三、计算题

求下列微分方程满足所给初始条件的特解.

班级_______________　姓名_______________　学号_______________

高等数学作业25　可降阶的高阶微分方程

一、填空题

1的通解是______________________________.

2.y″=cosx的通解是______________________________.

3.y″=e-2x的通解是______________________________.(www.chuimin.cn)

二、选择题

1.下列方程中（　）可用代换p=y′，p′=y″降为一阶微分方程.

2.微分方程式y″=y′的通解为（　）.

A.y=c1x+c2exB.y=c1+c2ex

C.y=c1+c2x　D.y=c1x+c2x2

三、计算题

1.求下列微分方程的解.

（1）（1+x2）y″=2xy′，y（0）=1，y′（0）=3

（2）y″-=xex

2.一曲线通过原点，且曲线上任意点的切线斜率为y-x，求此曲线的方程.

3.已知连续函数f（x）满足条件：，求f（x）.

班级_______________　姓名_______________　学号_______________

高等数学作业26　二阶常系数线性微分方程

一、填空题

1.微分方程y″-4y′+4y=0的两个线性无关的解是_____________.

2.若二阶常系数线性齐次方程的通解为y=C1e-2x+C2ex，则该方程为_____________.

二、选择题

1.y=c1ex+c2e-x（c1，c2为任意常数）是方程y″-y=0（　）.

A.通解　B.特解

C.不是所给方程的解　D.以上三者都不对

2.微分方程y″+2y′+y=0的通解是（　）.

A.y=c1cosx+c2sinx　B.y=c1ex+c2e2x

C.y=（c1+c2x）e-xD.y=c1ex+c2e-x

三、计算题

1.求下列微分方程的通解.

（1）y″+4y′=0　（2）y″-9y=0

（3）y″+4y′+4y=0　（4）y″-2y′+3y=0

2.求下列微分方程满足初始条件的特解.

（1）y″-3y′-4y=0，y|x=0=0，y′|x=0=-5

（2）y″+y=0，y|x=0=1，y′|x=0=1

班级_______________　姓名_______________　学号_______________

高等数学作业27　数项级数的概念和性质

一、选择题

二、写出下列级数的前4项（写在题的后面）

三、写出下列级数的一般项（写在题的后面）

四、根据级数的收敛与发散的定义，讨论下列级数的敛散性，如果收敛，并求其和

五、判别下列级数的敛散性

班级_______________　姓名_______________　学号_______________

高等数学作业28　正项级数及其审敛法

一、填空题

二、选择题

三、用比较审敛法判断下列级数的敛散性

四、用比值审敛法判断下列级数的敛散性

五、判断下列级数的敛散性

班级_______________　姓名_______________　学号_______________

高等数学作业29　任意项级数

一、填空题

二、选择题

三、判别下列级数是否收敛，如果是收敛的，是绝对收敛还是条件收敛

班级_______________　姓名_______________　学号_______________

高等数学作业30　幂级数

一、填空题

二、求下列幂级数的收敛区间

三、求下列幂级数的收敛域

四、利用幂级数性质求下列级数的和函数

班级_______________　姓名_______________　学号_______________

高等数学作业31　函数的幂级数展开

一、填空题

二、将下列函数展开成x的幂级数

1.f（x）=ln（1-x）.

2.f（x）=a3x（a＞0，a≠1）.

三、将f（x）=lnx展开成x-1的幂级数

四、将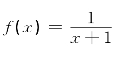展开成x-2的幂级数

五、将展开成x-1的幂级数

班级_______________　姓名_______________　学号_______________

高等数学作业32　拉普拉斯变换的概念

一、填空题

1.若，则象原函数f（t）=_________，象函数F（s）=_________.

2.设函数f（t）=2，则L［f（t）］=_________.

3.设f（t）是以T为周期的周期函数，f（t+T）=f（t），则L［f（t）］=_________.

二、求下列函数的拉普拉斯变换，并用查表的方法验证结果

三、求下列函数的拉普拉斯变换

班级_______________　姓名_______________　学号_______________

高等数学作业33　拉普拉斯变换的性质

一、填空题

1.若L［f（t）］=F（s），则L［f′（t）］=_____________.

2.已知，则L［f（t）］=_____________.

3.已知f（t）=t4e-2t，则L［f（t）］=_____________.

4.若L［f（t）］=F（s），则L［e-ktf（t）］=_____________.

二、求下列函数的拉普拉斯变换

班级_______________　姓名_______________　学号_______________

高等数学作业34　拉普拉斯逆变换

一、填空题

二、求下列函数的拉普拉斯变换

班级_______________　姓名_______________　学号_______________

高等数学作业35　拉普拉斯变换的应用

一、填空题

1.若L［f（t）］=F（s），则L［f″（t）］=_________________________________.

2.微分方程x′（t）-x（t）=0满足初始条件x（0）=1的解是_______________.

二、用拉普拉斯变换求下列微分方程满足初始条件的解

1.y″-2y′+y=0，y（0）=y′（0）=1.

2.y″+y′=e2t，y（0）=y′（0）=0.

3.y″-3y′+2y=4，y（0）=y′（0）=1.

三、用拉普拉斯变换解微分方程组

班级_______________　姓名_______________　学号_______________

高等数学作业36　行列式

一、选择题

1.设D是n阶行列式，则D=0的必要条件是（　）.

A.D中有两行（列）元素对应成比例　B.D中有一行（列）元素全部为零

C.D中各列元素之和为零　D.以D为系数行列式的齐次线性方程组有非零解

二、填空题三、判断题（在括号内填写“√”或“×”表示正确或不正确）

四、计算题

五、证明题

设行列式为，证明：当x=2或x=4时，此行列式为0.

班级_______________　姓名_______________　学号_______________

高等数学作业37　矩　阵（一）

一、填空题

二、选择题

1.设A为任意矩阵，则必为对称阵的是（　）.

A.A+ATB.AATC.A-ATD.（A+AT）T

2.设AT为A的转置矩阵，则下列命题中不正确的是（　）.

A.（AT）T=A　B.（A+B）T=AT+BT

C.（λAT）=λATD.（AB）T=ATBT

3.设A，B，C均为n阶方阵，则下列命题中不正确的是（　）.

A.（A+B）+C=A+（B+C）　B.（AB）C=A（BC）

C.AB=BA　D.A（B+C）=AB+AC

4.设A，B均为n阶方阵，则必有（　）.

A.det（AB）=det（A）det（B）　B.det（A+B）=det（A）+det（B）

C.（A+B）T=A+B　D.（AB）T=ATBT

6.设A，B为n阶方阵，A≠0，且AB=0，则（　）.

A.B=0　B.|B|=0或|A|=0

C.BA=0　D.（A-B）2=A2+B2

三、计算题

四、证明题

若A、B是n阶对称矩阵，则AB为对称矩阵的充分必要条件是AB=BA.

班级_______________　姓名_______________　学号_______________

高等数学作业38　矩　阵（二）

一、填空题

1.设A，B是同阶可逆方阵，则AB也可逆，且（AB）-1=_________.2.设A是3阶方阵，detA=3，则detA-1=_________.

二、判断题（在括号内填写“√”或“×”表示正确或不正确）

2.设A，B均为n阶方阵，且AB=0，则必有|A|=0或|B|=0.　（　）

3.两个方阵相等，则其行列式对应相等.　（　）

三、选择题

1.设n阶方阵A，B，C可逆且满足ABC=E，则必有（　）.

A.ACB=E　B.CBA=E　C.BAC=E　D.BCA=E

2.设A为n阶可逆方阵，则（A*）-1=（　）.

3.设A，B为同阶可逆矩阵，数λ≠0，则下列命题不正确的是（　）.

A.（A-1）-1=A　B.（λA）-1=λA-1

C.（AB）-1=B-1A-1D.（AT）-1=（A-1）T

四、计算题

1.已知，判别A是否可逆？若可逆，求出其逆矩阵.

2.已知，判别A是否可逆？若可逆，求出其逆矩阵.

3.解矩阵方程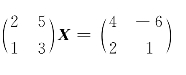：（X为二阶方阵）.

4.已知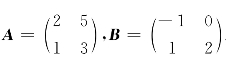.（1）求AT-2B；（2）若AX=B，求X.

5.化下列矩阵为简化行阶梯矩阵.

五、证明题

1.若n阶方阵A和B均可逆，则AB也可逆，证明（AB）-1=B-1A-1.

2.若A可逆，则A-1是唯一的.

3.如果矩阵A是可逆矩阵，证明detA≠0.

4.设A，B为同阶方阵，detA≠0，且AB=BA，求证：A-1B=BA-1.

5.设A2+A=E，证明A和A+2E都可逆，并求A-1及（A+2E）-1.

班级_______________　姓名_______________　学号_______________

高等数学作业39　矩　阵（三）

一、填空题

二、判断题（在括号内填写“√”或“×”表示正确或不正确）

1.若A有一个r阶非零子式，则r（A）=r.　（　）

2.若r（A）=9，则r（AT）=9.　（　）

三、求下列矩阵的秩

班级_______________　姓名_______________　学号_______________

高等数学作业40　线性方程组（一）

一、选择题

1.设A为m×n矩阵，则有AX=0非零解的充要条件是（　）.

A.r（A）=m　B.r（A）＜m　C.r（A）=n　D.r（A）＜n

2.以下结论正确的是（　）.

A.方程的个数小于未知量的个数的线性方程组一定有多解

B.方程的个数等于未知量的个数的线性方程组一定有唯一解

C.方程的个数大于未知量的个数的线性方程组一定无解

D.A、B、C都不对

二、计算题

1.用高斯消元法解线性方程组.

2.用高斯消元法解线性方程组.

3.用高斯消元法解线性方程组.

4.解线性方程组.

班级_______________　姓名_______________　学号_______________

高等数学作业41　线性方程组（二）

一、填空题

1.n元线性方程组AnnX=B，无解的充要条件是　_____________________；有惟一解的充要条件是______________________；有无穷多个解的充要条件是　______________________.

2.齐次线性方程组有非零解的充要条件是常数a为_________.

二、选择题

1.设线性方程组AX=B，则（　）正确.

A.若AX=0只有零解，则AX=B有唯一解

B.若AX=0有非零解，则AX=B有无穷多解

C.若AX=B有两个不同的解，则AX=0有无穷多解

D.AX=B有唯一解的充分必要条件是r（A）=n

2.设A为4×4矩阵，则AX=0有非零解的充要条件是（　）.

A.r（A）=4　B.r（A）=3　C.r（A）=5　D.r（A）＜4

三、判断题（在括号内填写“√”或“×”表示正确或不正确）

1.设A为m×n矩阵，则非齐次线性方程组AX=B有唯一解的充要条件是方程组AX=0只有零解.　（　）

2.有无穷多个解的非齐次线性方程组AX=B的通解形式不唯一.　（　）

3.AX=B有唯一解的充分必要条件是r（A）=n.　（　）

四、计算题

1.求齐次线性方程组的通解.

2.求齐次线性方程组的通解.

3.求非齐次线性方程组的通解.

4.求非齐次线性方程组的通解.

班级_______________　姓名_______________　学号_______________

高等数学作业42随机事件与概率

一、填空题

1.已知A⊂B，P（A）=0.2，P（B）=0.3，则P）=___________.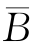

2.已知A、B满足P（AB）=P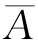B）=0.3，则P（B）=___________.

3.已知A、B相互独立，且P（A）=0.3，P（B）=0.2，则P（A）=___________.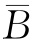

4.已知A、B互斥，且A与C相互独立，P（B）=0.2，P（A）=0.6，P（C）=0.3，则P（B+AC）=___________.

二、计算题

1.一个边长1米的立方体木块，表面全部涂上油漆，然后每边十等份锯开。随机抽出一块，求：

（1）两个面有油漆的概率？

（2）表面没有油漆的概率？

2.中国象棋盘由10×9条直线组成，象棋放在交叉点上。随意放上两个棋子，求它们在一条直线上的概率？

3.n个同学围坐一圈，求某两个同学恰好相邻的概率？

4.5封信，随机放入3个邮箱，求：

（1）某指定邮箱恰好放入2封信的概率？

（2）某指定邮箱为空的概率？

5.同时掷两个骰子，求出现的点数之和为8的概率？

6.袋中有4红5白共9个球，每次抽取1个，不放回，求：

（1）已知前2次抽的都是红球，则第3次抽红球的概率？

（2）则第3次才抽到红球的概率？

（3）则第3次抽到红球的概率？

7.电路由电阻A与两个并联的电阻B、C串联而成，设电阻A、B、C损坏的概率分别是0.3，0.2，0.2。求电路断开的概率？

8.3人独立地破译一份密码，已知每人能破译的概率分别为，求密码被破译的概率？

9.一个家庭有两个小孩，已知其中一个是男孩，求另一个也是男孩的概率？

10.一个小组7名同学，求至少有两个同学生日是同月的概率？

班级_______________　姓名_______________　学号_______________

高等数学作业43　随机变量与概率分布

一、填空题

1.某离散型随机变量的分布列为

则k=________.

2.某连续型随机变量Z～u［a，10］，其密度函数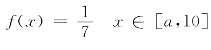，则a=_________.

3.已知X～N（2，4），则P（X＜2）=_________.

4.已知，则k=________.

二、计算题

1.一枚硬币掷三次，它正面出现的次数为X，求X的分布列.

2.5门炮同时向一艘敌舰各发射一发炮弹，每发炮弹的命中率为0.7，求击中敌舰炮弹个数X的分布列.

3.设X～P（x），且已知P（X=1）=P（X=2），求λ，且计算P（X=4）.

4.某人投篮，每次投中的概率为0.4，投中一次就结束，设投篮次数为X，求X的分布列.

5.某路公交车每隔8分钟发一辆车，某人随机来到车站，求等车时间不超过3分钟的概率.

6.设Z的概率密度为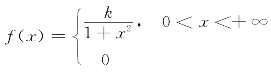，试确定k，并求P（0＜X≤1）.

7.设Z的密度函数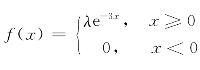，求：（1）λ的值；（2）P（X≤1）.

班级_______________　姓名_______________　学号_______________

高等数学作业44　随机变量的数字特征

一、填空题

1.若X、Y相互独立，则E（XY）=_________，D（X+Y）=_________.

2.若D（X）=3，则D（-2X+5）=________.

3.若E（X）=4，D（X）=1，则E（X2）=_________.

4.若X～N（6，2），则E（X）=_________，D（X）=_________.

二、计算题

1.已知X的分布列如下：

求E（X）与D（X）.

2.盒中有5只乒乓球，编号由1到5，在盒中同时取3只球，用X表示取出3只球的最大编号，求E（X）.

3.有n把看上去样子相同的钥匙，其中只有一把能打开门上的锁，用它们随机的逐一去开门，若每把钥匙试开后就除去，求试开次数X的期望.

4.设X1，X2相互独立，且X1的概率密度为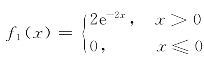，X2的概率密度为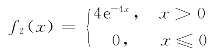，求：（1）E（X1+3X2）；（2）E（X1·X2）.

5.设X、Y相互独立，且X～P（3），Y～B（5，0.4），求D（3X-4Y）.

6.设X、Y相互独立，其概率密度分别为，fY（y）=，求D（X+Y）.

7.一台设备由三大部件构成，在其运转中各部件需要调整的概率都为0.1，各部件运行相互独立，以X表示同时需要调整的部件数，试求X的期望和方差.

8.设X、Y相互独立，且E（X）=E（Y）=1，D（X）=2，D（Y）=4，求E（X+Y2）.