首页理论教育结构力学-整体坐标系下单元刚度矩阵计算结果

结构力学-整体坐标系下单元刚度矩阵计算结果

2023-08-30 理论教育版权反馈

【摘要】：单元刚度矩阵是基于杆单元局部坐标系的，以杆轴线为x 轴，这样所有的单元都具有相同的单元刚度矩阵的形式。可以采用坐标变换的方法，将局部坐标系下的单元刚度矩阵转换至整体坐标系中。图9-4整体坐标系中的单元刚度矩阵K e。

单元刚度矩阵是基于杆单元局部坐标系的，以杆轴线为x 轴，这样所有的单元都具有相同的单元刚度矩阵的形式。但在实际结构中，各杆件的杆轴方向不可能相同。为了便于整体分析，必须选用一个公共坐标系，称为整体坐标系。为了区别，用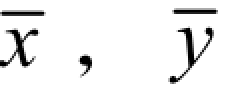 pagenumber_ebook=234,pagenumber_book=227 表示单元坐标系，用x，y 表示整体坐标系。

整体分析时，首先需要推导整体坐标系中的单元刚度矩阵K e。可以采用坐标变换的方法，将局部坐标系下的单元刚度矩阵转换至整体坐标系中。因此，首先讨论坐标系的转换矩阵。

1.单元坐标转换矩阵

图9-3 所示为单元 e，其局部坐标系为 pagenumber_ebook=235,pagenumber_book=228 ，整体坐标系为xOy。由x 轴到的夹角为α，以逆时针为正。

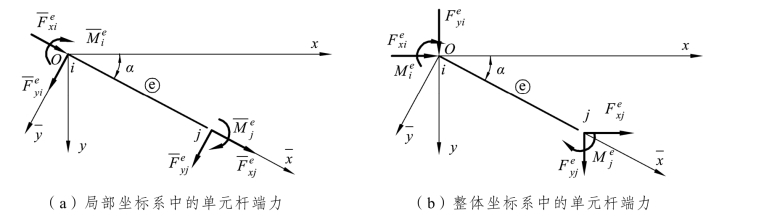
pagenumber_ebook=235,pagenumber_book=228

图9-3　单元杆端力的转换关系

pagenumber_ebook=235,pagenumber_book=228

将式（9-8）写成矩阵的形式：

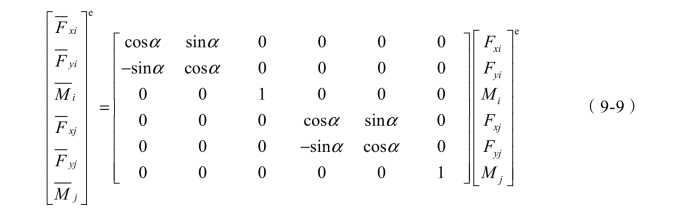
pagenumber_ebook=235,pagenumber_book=228

或简写成：

式中，T 称为单元坐标转换矩阵，即

pagenumber_ebook=236,pagenumber_book=229

可以证明，单元坐标转换矩阵T 为正交矩阵，其逆矩阵等于其转置矩阵，即

由式（9-10）可得：

pagenumber_ebook=236,pagenumber_book=229

2.整体坐标系中的单元刚度矩阵

整体坐标系中，单元杆端力与杆端位移的关系式同样可表示为：

式中，e

K 为整体坐标系下的单元刚度矩阵。

pagenumber_ebook=236,pagenumber_book=229

将式（9-10）、式（9-14）代入得

pagenumber_ebook=236,pagenumber_book=229

比较式（c）与式（9-15）可得：

pagenumber_ebook=236,pagenumber_book=229

（1）元素Kij表示整体坐标系下第 j 个杆端位移分量等于 1 时引起的第i 个杆端力分量。

（2）K e为对称矩阵。

（3）一般单元的K e为奇异矩阵。

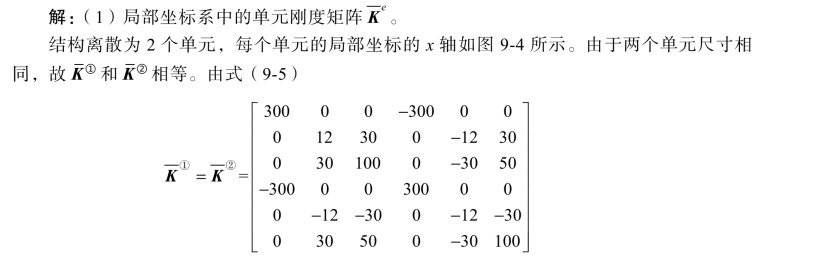
pagenumber_ebook=237,pagenumber_book=230

pagenumber_ebook=237,pagenumber_book=230

图9-4

pagenumber_ebook=237,pagenumber_book=230

（2）整体坐标系中的单元刚度矩阵K e。

单元①：α =0 ，T =I

单元②：α =90 °，单元②的转换矩阵为：

pagenumber_ebook=237,pagenumber_book=230

由式（9-16）可得单元②的刚度矩阵：

pagenumber_ebook=238,pagenumber_book=231