由式（7-6）、式（7-7）可知，轴向拉压杆在斜截面上有正应力和剪应力，它们的大小随截面的方位α角的变化而变化。当α＝0°时，正应力达到最大值：由此可见，拉压杆的最大正应力发生在横截面上。当α＝90°时，σα＝τα＝0，这表明在平行于杆轴线的纵向截面上无任何应力。......
2025-09-30
建筑力学第3版：等截面直杆转角位移方程
【摘要】：图15-30根据叠加原理，其杆端弯矩可分为图15-30、、、四种情况叠加，查表15-1得到：由A端转角θA引起的杆端力为由B端转角θB引起的杆端力为由两端相对侧移Δ引起的杆端力为如果有荷载作用，其固端弯矩、固端剪力为，根据叠加原理，将以上所得叠加有式就是两端固定的等截面单跨超静定梁的转角位移方程。可以将杆件分为图15-31、、三种情况叠加，查表15-1，同样方法可得图15-31式为一端固定，另一端铰支的等截面单跨超静定梁的转角位移方程。
在位移法中，确定基本未知量和基本结构以后，就可以将各杆段单独隔离出来分析，找出基本未知量和杆上的荷载与杆端内力的关系式，这样的关系式就是转角位移方程。
对于被隔离出来的单跨杆件，可以从表15-1中查到相应的项进行叠加，列出其转角位移方程。
表15-1 等截面直杆杆端弯矩和剪力
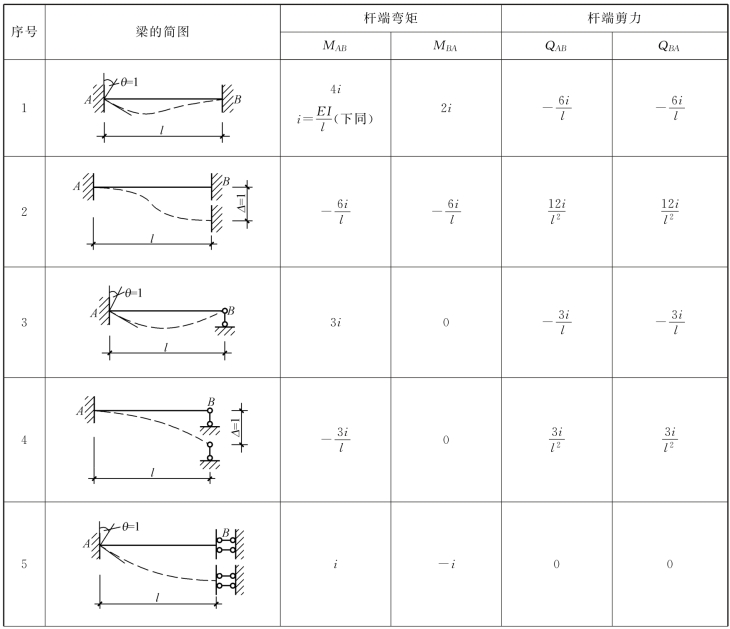
续表
1.两端固定杆件的转角位移方程
如图15-30（a）所示的杆件，两端固定，A发生转角θA，B发生转角θB，两端还发生有相对线位移Δ，同时杆上作用有荷载。
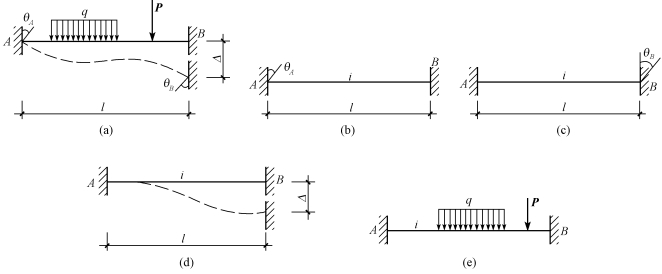
图15-30
根据叠加原理，其杆端弯矩可分为图15-30（b）、（c）、（d）、（e）四种情况叠加，查表15-1得到：
（1）由A端转角θA引起的杆端力为
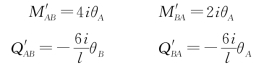
（2）由B端转角θB引起的杆端力为
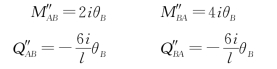(https://www.chuimin.cn)
（3）由两端相对侧移Δ引起的杆端力为
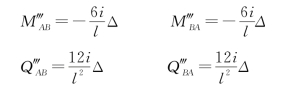
（4）如果有荷载作用，其固端弯矩、固端剪力为
，根据叠加原理，将以上所得叠加有
式（15-23）就是两端固定的等截面单跨超静定梁的转角位移方程。
2.一端固定另一端铰支杆件的转角位移方程
图15-31（a）所示的杆件，一端固定，另一端铰支，A发生转角θA，两端有相对线位移Δ，同时杆上作用有荷载。可以将杆件分为图15-31（b）、（c）、（d）三种情况叠加，查表15-1，同样方法可得
图15-31
式（5-24）为一端固定，另一端铰支的等截面单跨超静定梁的转角位移方程。
3.一端固定另一端定向支承杆件的转角位移方程
对于一端固定另一端滑动的杆件[图15-31（e）]，参考以上方法查表15-1，同样可以写出其转角位移方程：
相关文章
- 详细阅读
-
轴向拉（压）杆横截面上的应力|建筑力学（第3详细阅读
由此可得，横截面上各点处的正应力σ大小相等[图7-7]。若杆的轴力为N，横截面面积为A，则正应力为应力的单位为帕斯卡（简称帕），1帕＝1牛顿/平方米，或表示为1Pa＝1N/m2。由于前面已规定了轴力的正负号，由式（7-1）可知，正应力也随轴力N而有正负之分，即拉应力为正，压应力为负。直杆的横截面面积A＝10cm2，试计算各段横截面上的正应力。图7-8用截面法求出各段轴力：由式（7-1）计算各段的正应力值为......
2025-09-30
-
截面法求内力-建筑力学（第3版）详细阅读
图9-4求内力仍采用截面法。力Q和力偶矩M就是梁弯曲时横截面上产生的两种不同形式的内力，力Q称为剪力，力偶矩M称为弯矩。简支梁受载如图9-7所示，试用截面法求截面1—1上的内力。......
2025-09-30
-
建筑力学：支座移动时位移计算，第3版详细阅读
图14-21所示的刚架，支座移动为C1、C2、C3，致使整个结构移动到了虚线位置。将支座反力和对应的位移代入式，计算位移。由于A支座无位移，故只需计算B支座反力即可。计算结果为正，说明ΔCV与虚设单位力的方向一致。......
2025-09-30
-
建筑力学第3版：选择合理截面形状详细阅读
从弯曲强度方面考虑，最合理的截面形状是用最少的材料获得最大的抗弯截面模量。梁的强度一般由横截面上的最大正应力控制。当弯矩一定时，横截面上的最大正应力σmax与抗弯截面模量Wz成反比，Wz越大就越有利。而Wz的大小与截面的面积及形状有关，合理的截面形状是指在截面面积A相同的条件下，有较大的抗弯截面模量Wz。所以，I形、槽形截面比矩形截面合理，矩形截面立放比平放合理，正方形截面比圆形截面合理。......
2025-09-30
-
建筑力学第3版-临界应力总图-压杆计算公式详细阅读
如果将压杆的临界应力根据其柔度不同而分别计算的情况用一个简图来表示，该图形就称为压杆的临界应力总图。图11-9与图11-10即某塑性材料的临界应力总图。由临界应力总图可以看出，Q235钢应在λ＝0～123时用抛物线形经验公式计算临界应力，在λ＞123时用欧拉公式计算临界应力。......
2025-09-30
-
压杆稳定条件的应用与建筑力学（第3版）相关详细阅读
即已知压杆的几何尺寸、所用材料及支承条件，按稳定条件计算其能够承受的许用荷载值F。在稳定条件式中，已知φ后才能标出A值，但在杆件尺寸未确定之前，无法确定λ值，因而也就无法确定φ值，故可采用试算的方法。然后，根据截面尺寸及杆长计算出柔度λ，由λ查出φ，再以算得的面积A和查得的φ值验算其是否满足稳定条件。......
2025-09-30
-
《建筑力学第3版》-细长压杆临界力计算详细阅读
以上讨论的是两端铰支的细长压杆的临界力计算。对于其他支承形式的压杆，也可用同样方法导出其临界力的计算公式。因此，可将两端铰支约束压杆的挠曲线形状取为基本情况，而将其他杆端约束条件下压杆的挠曲线形状与之进行对比，从而得到相应杆端约束条件下压杆临界力的计算公式。表11-1各种支承约束条件下等截面压杆临界力的欧拉公式以上讨论的都是理想的支承情况。现分别计算两种截面杆的临界力。......
2025-09-30
相关推荐