首页理论教育闭环系统中的M圆、θ圆和尼氏图

闭环系统中的M圆、θ圆和尼氏图

2023-06-28 理论教育版权反馈

【摘要】：图5-63等M圆在M圆中，当M变为无穷大时，圆缩小为点。例如，当系统放大系数K=K1时，闭环系统将有谐振峰值Mp=M1，谐振角频率为ωp1。

为了便于用闭环频率特性的指标Mp、ωp来分析和设计系统，常采用直角坐标的等M图和对数坐标的等M图。

1.闭环系统等幅值M的轨迹

设开环频率特性

WK(jω)=P(ω)+jQ(ω)

则闭环系统频率特性的幅值可写成

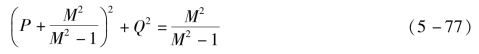
pagenumber_ebook=161,pagenumber_book=150

整理得

pagenumber_ebook=161,pagenumber_book=150

当M=1时，式（5-77）变为

2P+1=0

这是平行于虚轴的直线，通过 pagenumber_ebook=162,pagenumber_book=151 点。

如果M=1，则对一个给定的M值，式（5-77）在WK（jω）平面上描绘出一个圆，这就是等M圆，如图5-63所示。

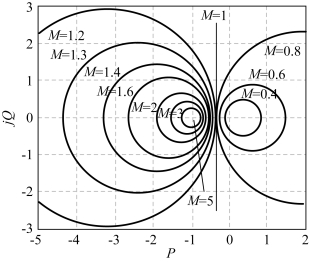
pagenumber_ebook=162,pagenumber_book=151

图5-63　等M圆

在M圆中，当M变为无穷大时，圆缩小为（-1，j0）点。这说明，当Mp为无穷大时，系统处于不稳定的边缘。M＞1的圆位于M=1线的左侧，而M＜1的圆位于M=1线的右侧。

如果在WK（jω）平面上绘出系统开环幅相频率特性和等M圆，则由幅相频率特性与等M圆的切点可以确定闭环系统的谐振频率ωp和谐振峰值Mp。

图5-64中示出了等M圆和系统开环幅相频率特性。例如，当系统放大系数K=K1时，闭环系统将有谐振峰值Mp=M1，谐振角频率为ωp1。如果放大系数增加到K=K2，则谐振峰值增加到Mp=M2，谐振角频率为ωp2。当K增加到K3时，WK（jω）通过（-1，j0）点，Mp=∞系统处于稳定边界。

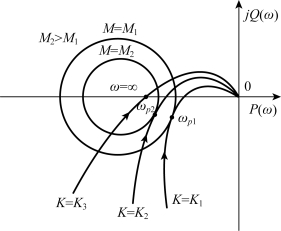
pagenumber_ebook=162,pagenumber_book=151

图5-64　开环频率特性与谐振峰值之间的关系

2.闭环系统等相角轨迹（等θ圆）

闭环系统的相角为

两边取正切，整理得

pagenumber_ebook=163,pagenumber_book=152

为书写方便，令N=tanθ（ω），得

pagenumber_ebook=163,pagenumber_book=152

当N为给定值时，上式代表一簇圆，圆心为，半径为这就是等θ，如图5-65所示。

pagenumber_ebook=163,pagenumber_book=152

图5-65　等θ图

将开环频率特性WK（jω）和等θ圆绘于同一图中，就可以利用开环频率特性求出闭环频率特性相角θ与角频率ω之间的关系。

3.尼柯尔斯图线

将直角坐标的等M圆和等θ圆逐点转移到对数幅相平面上，得到尼柯尔斯图线，简称尼氏图。在对数幅相平面上，横坐标为开环系统的相角，以普通比例尺标度；纵坐标为开环系统的对数幅值，仍表示为普通比例尺。

下面介绍用分析法求尼氏图的方法。

设一个单位反馈系统的开环频率特性为WK（jω），则闭环频率特性为

pagenumber_ebook=163,pagenumber_book=152

令WK（jω）=A（ω）ejφ（ω），简写为WK（jω）=Aejφ，于是

pagenumber_ebook=163,pagenumber_book=152

则

pagenumber_ebook=164,pagenumber_book=153

据式（5-78）和式（5-78）可在尼柯尔斯图的坐标平面上画出等M（ω）dB曲线和等θ（ω）曲线，然后在尼氏图上绘出开环对数幅相频率特性，便不难求得系统的谐振峰值Mp、谐振频率ωp和频带宽ωb。

例5-13 绘制例5-5中系统的尼柯尔斯图，确定系统的谐振峰值和谐振角频率。

解：在图5-26所示开环对数频率特性中，对于每一个ω值，都对应一对L（ω），φ（ω）值，相应地布尼氏图上得到一点。连接不同频率值时的各点，就可以得到尼氏图上的开环对数幅相频率特性曲线，如图5-66中实线所示。

pagenumber_ebook=164,pagenumber_book=153

图5-66　系统的尼氏图

开环对数幅相频率特性曲线与M（ω）=3.88dB的等M线相切，则相应闭环系统的谐振峰值Mp=3.88dB，对应的谐振频率ωp=1.98rad/s。带宽ωb是M（ω）=-3dB对的角频率，从图5-66中可看到曲线与-3dB的等M线的交点对应的角频率就是带宽ωb，ωb=3.96rad/s。ωp，ωb可结合伯德图来求取：在尼氏图上找到Mp=3.88dB和M（ω）=-3dB对应的开环对数幅值L（ω），然后在伯德图上找到相应的角频率。

从尼氏图可以看出，在改变开环系统放大系数时，开环系统的相角不变，而只改变其幅值。所以在对数幅相特性上，WK（jω）的曲线只有上下移动，这样就能很方便地看出改变开环放大系数对闭环系统谐振峰值、谐振角频率和频带宽的影响。