黏聚裂纹模型探究

2025-09-29 理论教育版权反馈

【摘要】：矢量b＋和bα可以表示为2.黏聚应力与软化曲线黏聚裂纹模型主要开裂方式是Ⅰ型裂纹。单元的破坏准则采用最大拉应力的破坏准则，当黏聚应力高于拉伸强度时，开始计算裂纹张开位移。黏聚裂纹模型计算时，裂纹必须沿单元寻找其路径，在这些被选中的单元中，最大主应力至少应超过拉伸强度一次。

黏聚裂纹模型是在Hillerborg 等［15］早期工作的基础上发展而来的，基本理论框架由西班牙马德里理工大学的Elice 和Planas 教授基于强间断理论提出，可准确预测混凝土材料的断裂失效过程，后来在陶瓷、金属、PMMA 以及PBX 其他脆性及准脆性材料上有广泛应用［16～20］。

1.强间断理论

强间断法将不连续问题转化成连续问题进行研究，在计算材料的开裂和滑移中有较广泛的应用，可以针对多种材料的位移间断进行应用。强间断法是指位移场和应变场都是不连续的，如图3－7 所示，并且在强间断面的两侧必须满足拉应力的连续性。为了在有限元框架中模拟裂纹导致的位移间断行为，引入Heaviside 强化函数和裂纹尖端强化函数以考虑裂纹对单元位移场的影响。这种方法可以不改变单元网格和节点布置，通过修改单元形函数，对节点的位移进行扩展，来实现裂纹间断的嵌入。

pagenumber_ebook=69,pagenumber_book=49

图3－7　强间断法二维单元示意图

强间断法将位移场解耦为连续部分和非连续部分，连续部分描述单元的一般变形行为，非连续部分表示强间断附加的自由度，可表示为位移阶跃矢量w。当裂纹张开时，单元被间断线分离成A－和A＋两个区域。那么，定义垂直于裂纹张开方向的单位法向矢量n 和位移阶跃矢量w。假设沿裂纹线嵌入单元中的位移阶跃矢量w 的大小等于裂纹两侧的位移场之差。

根据强间断理论，该单元的位移场可以由一个连续的位移场uα和一个间断位移场w 叠加而成，即

式中：；H（x）为Heaviside 函数，可以表示为

pagenumber_ebook=69,pagenumber_book=49

应变张量εα（x）是单元的表观应变张量，可由总的节点位移获取，直接从施加在节点位移上的形函数求导得到

式中：εα（x）是由连续体单元的应变εc（x）和在裂缝线上的狄拉克－δ 函数（Dirac delta function）的叠加，即

式中：εc（x）表示单元中不存在位移间断时的应变场，矢量b＋定义为A＋区域内所有节点对应形函数的梯度之和。

根据式（3－75），在裂缝两端连续体单元的应变张量εc（x）可以表示为

式中：上标s 表示张量的对称部分。

矢量b＋和bα可以表示为

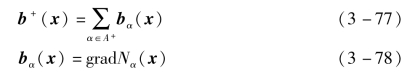
pagenumber_ebook=70,pagenumber_book=50

2.黏聚应力与软化曲线

黏聚裂纹模型主要开裂方式是Ⅰ型裂纹。采用一个简单概括性的混合裂纹模型，该模型假设裂缝面上的黏聚应力t 平行于裂纹张开位移，则

黏聚应力一般为虚拟裂缝张开位移的函数。f（｜w ｜）为软化曲线函数，用来表征材料的裂纹张开位移与黏聚应力的关系，如图3－8 所示。在卸载作用下，假设黏聚应力线性降为原点，则式（3－79）可以写为

pagenumber_ebook=70,pagenumber_book=50

式中：＝max（｜w｜）为裂纹张开位移，等于裂纹历史最大张开位移。

单元的破坏准则采用最大拉应力的破坏准则，当黏聚应力高于拉伸强度时，开始计算裂纹张开位移。当裂纹张开位移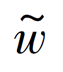 pagenumber_ebook=70,pagenumber_book=50 达到临界值后，裂缝两端应力减为0。软化曲线下方的面积即材料的断裂能，其意义是形成单位面积裂缝所吸收的能量。软化函数可被认为是与几何形状和尺寸无关的材料属性，决定了断裂过程能量耗散的分配。

3.基本方程

为了计算单元中的应力，如图3－9 所示，在裂纹路径上的应力为

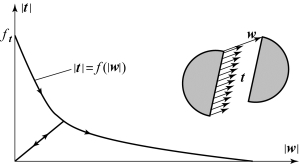
pagenumber_ebook=71,pagenumber_book=51

图3－8　黏聚裂纹模型中软化曲线示意图

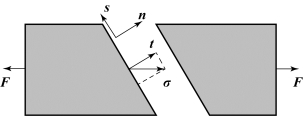
pagenumber_ebook=71,pagenumber_book=51

图3－9　黏聚应力示意图

pagenumber_ebook=71,pagenumber_book=51 (https://www.chuimin.cn)

图3－10 所示为常应变三角形单元示意图。如图3－10 （a）所示，在含有强间断线（裂缝）中，沿着孤立节点正法线方向，可以得到

式中：h 为孤立节点相对的角度对应的单元边的高度；n＋为这条边的单位法向矢量。

pagenumber_ebook=71,pagenumber_book=51

图3－10　常应变三角单元［16］

（a）几何形状；（b）潜在裂纹路径（虚线）

在局部平衡模式下n＋＝n，满足该关系的条件：一是强间断的位置（裂纹）平行于单元的任意边；二是裂纹位置在边长1／2 处，如图3－11 （b）所示为满足该平衡关系的潜在裂纹路径。式（3－81）可以写为

联立式（3－80）和式（3－83），可得

pagenumber_ebook=71,pagenumber_book=51

在裂纹产生前，假设材料行为是线弹性的。此时，描述材料行为的关系为

式中：E 为材料的弹性模量四阶张量。

将式（3－76）代入式（3－85），可得

将式（3－84）代入式（3－86），可得

pagenumber_ebook=72,pagenumber_book=52

式（3－87）可改写为

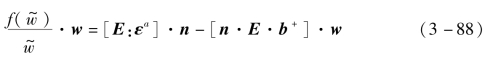
pagenumber_ebook=72,pagenumber_book=52

或

pagenumber_ebook=72,pagenumber_book=52

式中：1 是二阶单位矢量。

式（3－88）和式（3－89）为求解裂纹张开位移张量的基本控制方程，采用牛顿－拉夫森（Newton－Raphson's method）迭代法求解。在这个过程中，b＋和n 求解也至关重要。

4.起裂判据

裂纹起裂和裂纹方向采用最大主应力准则。一旦单元的最大主应力超过拉伸强度，即引入垂直于最大主应力方向的裂纹。采用最大主应力判据作为起裂和裂纹扩展判据便于处理复杂的断裂模式，如裂纹分支、复杂断裂面的裂纹传播。Gray 等的实验结果表明，单轴压缩下，临界拉伸起裂判据仍是PBX 炸药主导的失效判据。因此，裂纹方向矢量n 是该最大主应力对应的单位特征矢量。

在所有可能的孤立节点组合及其导致的矢量b＋中，确定孤立节点只需要矢量n 与矢量b＋的夹角尽可能小，即

pagenumber_ebook=72,pagenumber_book=52

5.裂纹调整技术

从前面描述中可以发现，黏聚裂纹模型是在单元尺度实现的，是严格局部的，不需要强制使含裂纹的连续保持全局连续性。黏聚裂纹模型计算时，裂纹必须沿单元寻找其路径，在这些被选中的单元中，最大主应力至少应超过拉伸强度一次。然而，在裂纹尖端存在复杂的应力场，高应力可能会使得单元中的裂纹方向明显不同于邻近单元的裂纹方向，从而导致裂纹锁定。另外，单元裂纹方向预测不准确，也会发生裂纹锁定，没有强制的裂纹连续性或者预先定义裂纹区域，如图3－11 所示。

pagenumber_ebook=73,pagenumber_book=53

图3－11　裂纹自锁示意图［28］

为了避免这类问题，使用了裂纹调整算法。其思想是当断裂能没有超过阈值前，裂纹的方向可以调整。在有限元计算时，网格尺寸大小是不同的，计算矢量b＋非常复杂，因为需要给予子程序各个单元所有节点的坐标。在计算中，前一个时间步裂纹面的法向矢量存为历史变量，计算当前时间步的法向矢量，并评估两个法向矢量之间的角度。角度越小，找到矢量b＋的更好选择的概率越小。如果前一个时间步和当前时间步之间的角度小于给定的阈值，就忽略裂纹调整。该算法可以在给出满意精度的前提下明显降低计算成本。

如果法向矢量之间的角度足够大，裂纹调整就开始起作用。裂纹法向矢量n 和矢量b＋重新计算更新。计算裂纹张开矢量，并与临界裂纹张开位移值w 进行比较。一旦裂纹张开矢量超过裂纹调整阈值，裂纹法向矢量n 和矢量b＋就不再变化，也不允许再调整裂纹方向。

计算时为了旋转裂纹，需要给定裂纹调整的临界张开位移值和法向矢量允许变化的最小角度。作为参考，裂纹调整的临界张开位移值为（0.1～0.2）·GF／ft，其中GF为断裂能，ft为拉伸强度。

黏聚裂纹模型探究

相关推荐