【摘要】:图2-1床沙质含沙量与无量纲单位水流功率参数的关系为了说明大水深河流和水深较小的实验室水槽中输沙能力的不同,图2-1点绘了床沙质含沙量与无量纲的单位水流功率参数的关系。小水深水槽试验和大水深河流雷诺数的差别达到两个数量级,这种差别必然会影响到水流阻力和与之相关的泥沙输移过程。图2-3的结果再次说明,由于实验室水槽的水深变化范围有限,依据实验室水槽资料建立的输沙关系,不能够代表大河流的输沙关系。
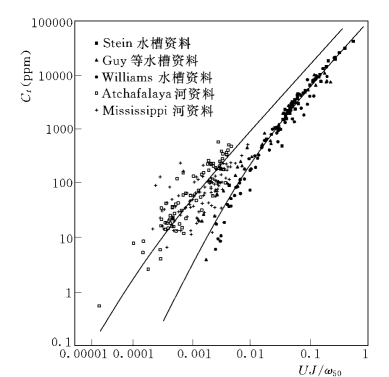
图2-1 床沙质含沙量与无量纲单位水流功率参数的关系
为了说明大水深河流和水深较小的实验室水槽中输沙能力的不同,图2-1点绘了床沙质含沙量与无量纲的单位水流功率参数的关系。图中无量纲的单位水流功率定义为UJ/ω50,其中U 为流速,J 为能坡,ω50为相应床沙中值粒径的沉速。乘积UJ 称为单位水流功率 (Yang,1973;Bettess& White,1987),代表单位重量水体的水流功率 (等于γQLJ/γBh L,Q为流量,L 为河段长度,B 为河宽,γ 为水的容重)。图2-1 中的实验室水槽资料包括Stein、Guy等以及Williams的试验资料,大河流资料为Atchafalaya河和Mississippi河St.Louis实测资料。水槽试验的水深均小于0.37m,大河流资料的水深范围从4.66~17.28m。可以看到,水槽资料和大河流资料分别具有两条不同的趋势曲线,对于给定的无量纲单位水流功率参数UJ/ω50而言,大河流的床沙质含沙量比小水深水槽的含沙量要高得多。
图2-2点绘了实验室水槽和天然河流的雷诺数与UJ/ω50的关系。可以看出,对于水槽资料,雷诺数的变化范围为50000~500000,而对于大河流资料,雷诺数的变化范围为2×106~1×108。图中没有给出中等水深河流的资料,实际上中等水深河流的资料落在两者之间。小水深水槽试验和大水深河流雷诺数的差别达到两个数量级,这种差别必然会影响到水流阻力和与之相关的泥沙输移过程。
下面以Engelund-Hansen (1967)公式为例,进一步说明大河流与实验室水槽输沙规律的不同。Engelund-Hansen公式不仅形式简单,而且推导过程具有一定的理论基础,在实际中也得到了广泛应用。该式可表示为:

式中:Φ 为无量纲的输沙强度参数;θ 为无量纲的剪切力强度参数;fE为Engelund-Hansen所定义的阻力系数。
图2-3以Φ/θ2.5和fE为参数,将大河流和水槽试验的输沙数据点绘在同一张图上。可以看到,水深小于0.5m 的水槽试验与水深超过4m 的大河流相比,数据点显然具有不同的关系。图2-3的结果再次说明,由于实验室水槽的水深变化范围有限,依据实验室水槽资料建立的输沙关系,不能够代表大河流的输沙关系。










相关推荐