贝叶斯网络是基于概率分析和图论对不确定性知识进行表示的推理模型，它是一种模拟人类推理过程中因果关系的不确定性处理模型。贝叶斯分类器是用于分类的贝叶斯网络，它是各种分类器中分类错误概率最小或者在预先给定代价的情况下平均风险最小的分类器。通过对纽约市曼哈顿区2014年至2017年的交通事故数据构造朴素贝叶斯网络，对事故中伤亡人数进行分析。图4.1相关性分析结果......
2025-09-29
全局自相关分析方法探讨
【摘要】：全局莫兰指数I是评价全局自相关性最常用的指标。全局莫兰指数I需要进行零假设检验，首先假定研究对象不存在空间相关性，然后通过Z得分检验来验证假设是否成立。表5.2全局自相关分析结果图5.9是2020年新冠肺炎确诊病例率全局自相关莫兰散点图，每个点代表了一个街区的集聚类型，第一象限为高-高集聚区，第二象限为低-高聚集区，第三象限为低-低集聚区，第四象限为高-低集聚区。
全局莫兰指数I是评价全局自相关性最常用的指标。其计算公式如下:
莫兰指数I的取值范围为(－1，1)，如果值为正表示空间对象的属性值的分布具有正相关性，负值表示该空间对象的属性值分布具有负相关性，0则表示空间对象的属性值不存在空间相关，即空间随机分布。
全局莫兰指数I需要进行零假设检验，首先假定研究对象不存在空间相关性，然后通过Z得分检验来验证假设是否成立。Z得分可以由莫兰指数I系数及其期望值和方差计算得到:
在零假设条件下(即不存在空间相关性)，期望值为:
当n趋于无穷大时，期望值为0。莫兰指数I的方差有两个假设:空间对象属性取值的正态分布假设和空间对象随机分布假设。当为正态分布时，方差为:(https://www.chuimin.cn)
一般情况下，当｜Z｜＞1.96时，拒绝零假设，即在95%的概率下认为存在着空间自相关性。
以2025年12月下半月至2025年3月上半月这一时间段美国纽约市177个街区的新冠肺炎发病率数据为数据源进行全局自相关分析，每半个月为一个时间周期，分析结果见表5.2。从表5.2可以看出，莫兰指数I的值均大于0，且｜Z｜＞1.96，说明发病率数据呈现出明显集聚特征，P值为0.001，则说明这组数据随机生成的概率很小。莫兰指数I指数值范围在0.7439～0.79525之间，表示纽约街区的新冠肺炎发病率存在正向的自相关关系。
表5.2 全局自相关分析结果
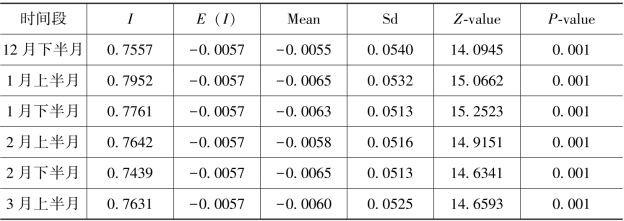
图5.9是2025年新冠肺炎确诊病例率全局自相关莫兰散点图，每个点代表了一个街区的集聚类型，第一象限为高-高集聚区，第二象限为低-高聚集区，第三象限为低-低集聚区，第四象限为高-低集聚区。大部分点位于一、三象限，斜率为正，表示正的空间自相关性。
图5.9 莫兰指数I散点图
相关文章
- 详细阅读
-
线性相关性分析方法简介详细阅读
相关性分析可以分为线性相关分析、偏相关分析、距离分析等。对交通事故与相关要素之间相关性进行计算时，由于数据不符合正态分布，所以选择Kendall相关系数、Spearman相关系数分析计算，得到Kendall及Spearman相关系数分析结果见表4.3，依次表示事故伤亡等级、日夜、季节、假期、风速、温度、天气、酒精、车速、大型车辆之间的相关系数和显著性。表4.3Kendall及Spearman相关系数分析结果......
2025-09-29
-
趋势面分析方法论详细阅读
趋势面分析只考虑空间因素，利用数学曲面模拟地理要素在空间上的分布及变化，适于模拟大范围空间分布，检测总趋势和与趋势的最大偏离。例如，对纽约市的交通事故数据进行趋势面分析。随后，根据格网数据提取格网点，进行趋势面分析，如图3.18所示，图为按照交通事故发生次数进行的趋势面分析，图为按照交通事故的死亡人数进行的趋势面分析。......
2025-09-29
-
功率类型及相关测量方法详细阅读
在直流电路中，直流电源提供的功率全部为有功功率。有功功率与视在功率的比值称为功率因数，用cosφ表示，cosφ=P/S。为了减少电动机的无功功率，应选用合适的功率，避免出现“大牛拉小车”或让电动机空载运行的情况。图2-12 用电压表和电流表测量功率的两种测量电路......
2025-09-29
- 详细阅读
- 详细阅读
- 详细阅读
- 详细阅读
相关推荐