计算机视觉测量系统是计算机视觉技术在测量领域中的延伸,因此两者的结构基本相同。图1.8 典型的视觉测量系统......
2023-11-24
边缘检测的功能是检测出图像中的边缘像素点。由于噪声、不均匀光照及其他原因引入的干扰会产生边缘间断和伪边缘点,使得实际的边缘像素很少能完整描述成一条边缘。因此,在边缘检测之后要进行边缘连接,将边缘像素组合成有意义的边缘。边缘连接包含两方面含义:
1)剔除噪声点,保留真正的边缘点。
2)填补边缘空白点。
1.局部处理方法
边缘连接最简单的方法之一是分析图像中每个边缘像素点(x,y)的邻域,如3×3或5×5邻域内像素的特点。将所有依据预定准则被认为是相似的点连接起来,形成由共同满足这些准则的像素组成的一条边缘。在这种分析过程中,确定边缘像素相似性的两个主要性质:
1)用于生成边缘像素的梯度算子的响应强度,有

则处于定义的(x,y)邻域内坐标为(x0,y0)的边缘像素,在幅度上相似于位于(x,y)的像素,这里E是一个非负门限。
2)梯度矢量的方向(角度)由梯度矢量的方向角给出,如果

则处于定义的(x,y)邻域内坐标为(x0,y0)的边缘像素具有与(x,y)的像素相似的角度。这里A是非负门限。如前所述(x,y)处边缘的方向垂直于此点处梯度矢量的方向。
如果大小和方向准则得到满足,则在(x,y)邻域中的点就与位于(x,y)的像素连接起来。在图像中的每个位置重复这一操作。当邻域的中心从一个像素转移到另一个像素时,这两个相连接点必须记录下来。
2.边界跟踪
边界跟踪(Boundary Tracking)也称轮廓提取、轮廓跟踪,是由梯度图中一个边缘点出发,以此搜索并连接相邻边缘点从而逐步检测出边界的方法,其目的是区分检测目标与背景。一般情况下,边界跟踪算法具有较好的抗噪性,产生的边缘具有较好的刚性。与边缘检测技术相比,图像边界跟踪技术只需要对图像的外部边缘进行跟踪,而边缘提取技术不但需要提取图像的外部边缘,还需要提取图像的内部边缘。
根据边缘的特点,有的边界取正值(例如阶跃型边缘的一阶倒数为正)有的取负值(例如屋顶形边缘的二阶导数,有的边界取0值(阶跃型边缘二阶导数,屋顶形边缘一阶导数均过零点),因此可以将轮廓提取算法分为极大跟踪法、极小跟踪法、极大-极小跟踪法与过零点跟踪法。轮廓跟踪过程大致可以分为三步:
1)确定轮廓跟踪的起始边界点。其中起始边界点可以是一个也可以是多个。
2)确定和采取一种合适的数据结构和搜索策略,根据已经发现的边界点确定下一个检测目标并对其进行检测。
3)确定搜索终结的准则或终止条件(如封闭边界回到起点),并在满足条件时停止进程,结束搜索。
常用的轮廓跟踪技术有两种:探测法和梯度图法。假设图像为二值图像且图像边缘明确,图像中只有一个具有封闭边界的目标,那么探测法的基本步骤如下:假设k为记录图像轮廓线像素点数的变量,其初始值为0。
1)自上而下、自左到右扫描图像,发现某个像素p0从0变到1时,记录其坐标(x0,y0),k=0。
2)从像素(xk,yk-1)开始按逆时针顺序研究其8像素邻域,将第一次出现像素值为1的像素记为pk,并存储其坐标(xk,yk),置k=k+1。像素(xk,yk)的逆时针8-邻域依次为(xk,yk-1)、(xk-1,yk-1)、(xk-1,yk)、(xk-1,yk+1)、(xk,yk+1)、(xk+1,yk+1)、(xk+1,yk)、(xk+1,yk-1)。
3)判断pk与p0是否是同一个点,即xk是否等于x0,yk是否等于y0。如果直到pk与p0是同一个点,则算法结束,否则返回步骤2)继续跟踪。
【例4.6】 探测法轮廓跟踪实例
原始的二值图像由图4.27a所示。按照探测法的基本过程进行图像轮廓探测。
1)从左上角开始扫描图像,直到找到第一个非0像素p0,记录其坐标x0=1,y0=2,如图4.27b所示。
2)逆时针研究p0的8-邻域(如图4.27b所示,其中虚线框表示的像素p0是8-邻域的第一个像素),可以发现p1,记录其坐标x1=2,y1=3,如图4.27c所示。
3)逆时针研究p1的8-邻域,可以发现p2,记录其坐标x2=3,y2=4。
4)逆时针研究p2的8-邻域,可以发现p3,记录其坐标x3=2,y3=5。
5)逆时针研究p3的8-邻域,可以发现p4,记录其坐标x4=2,y4=6。
6)逆时针研究p4的8-邻域,可以发现p5,记录其坐标x5=2,y5=7。

图4.27 探测法轮廓跟踪
7)逆时针研究p5的8-邻域,可以发现p6,记录其坐标x6=3,y6=6。
8)逆时针研究p6的8-邻域,可以发现p7,记录其坐标x7=4,y7=6。
9)逆时针研究p7的8-邻域,可以发现p8,记录其坐标x8=5,y8=6。
10)逆时针研究p8的8-邻域,可以发现p9,记录其坐标x9=6,y9=5。
11)逆时针研究p9的8-邻域,可以发现p10,记录其坐标x10=6,y10=4。
12)逆时针研究p10的8-邻域,可以发现p11,记录其坐标x11=6,y11=3。
13)逆时针研究p11的8-邻域,可以发现p12,记录其坐标x12=5,y12=3。
14)逆时针研究p12的8-邻域,可以发现p13,记录其坐标x13=4,y13=2。
15)逆时针研究p13的8-邻域,可以发现p14,记录其坐标x14=3,y14=2。
16)逆时针研究p14的8-邻域,可以发现p15,记录其坐标x15=2,y15=2。
最终的轮廓如图4.27d所示。
上述边界跟踪法过程比较简单,适用于图像边缘连接明确的情况。然而,实际应用中很多图像的边缘连接并不明显,这时可以采用最大梯度跟踪法进行边界跟踪,其基本步骤可以如下描述:
1)计算图像的梯度图,从梯度图中选出梯度最大的点作为边界跟踪的第一个起始点。
2)第一个起点的8-邻域中选梯度最大的点作为第二个边界点。8-邻域像素的分析采用逆时针方向搜索,并假设目标在边界跟踪方向的左方。
3)以已经确定的两个边界点分别作为当前边界点C和前一个边界点P,每次在以当前边界点C为中心的3×3邻域中选取下一个边界点。根据C点和P点的位置不同,可得到如图4.28所示的8种组合。这里为保证边界的光滑性,每次只在标有阴影的三个候选像素中根据梯度值的大小选取下一个边界点。这样得到的边界为8-邻域连通,且没有大于45°的转折(最小曲率半径是1.5个像素)。

图4.28 8种搜索窗口
4)以上一部确定的当前边界点C作为新的前一个边界点P,而以刚确定的新边界点作为新的当前边界点C。继续搜索直到边界闭合为止。继续搜索直到梯度绝对值小于一个阈值时,搜索停止。
基于梯度图的边界跟踪适用于噪声较小图像,可确定出目标具有最大梯度的边界,也可用于将分割出的区域边界找出来。当图像中噪声较大时,会出现偏离正确边界或失踪或跑出图像范围的情况,此时可先对梯度图进行平滑然后再开始搜索。
【例4.7】 增强抗噪能力的方法——“跟踪虫”法
如图4.29所示,跟踪虫是一个长方形的平均窗口模板,其中各元素一般具有相同的值,模板后部以当前像素为中心,其轴沿当前搜索方向。在每个搜索位置都计算模板下所有像素的平均梯度,然后选模板前部具有最大平均梯度值的位置作为下一个边界位置。这种方法可看作是利用上述利用八种搜索窗口方法的一个大模板推广。模板越大,对梯度的平滑作用越强,抗噪声能力也越强。这种方法也可限定边界不能急速地变化方向。

图4.29 边界跟踪平均窗口模板
3.Hough变换及线、圆检测
(1)Hough变换及直线检测
如果图像分割过程中,预先已经知道目标的形状(直线、曲线、圆等),则可以利用Hough(哈夫或霍夫)变换进行检测。Hough变换的基本思想是,建立一种点-线的对偶性关系,将图像数据从图像空间变换到某个参数空间,通过分析参数空间上的参数分布情况来实现目标的检测。利用Hough变换可以直接分割出某些已知形状的目标,并且受噪声和曲线间断的影响较小。下面以直线的Hough变换为例对其基本原理进行介绍。
在图像空间的直角坐标系里,经过点(x,y)的所有直线均可由下式表示:
y=px+q (4.65)
式中,(x,y)为图像空间上的点;(p,q)为参数空间上的点,即p为斜率,q为截距。将式(4.66)经过适当的变形后,可以表示为
q=-px+y (4.66)
与式(4.65)相对应,式(4.66)可以认为是参数空间里经过点(p,q)的一条直线。
假设(xi,yi)和(xj,yj)分别为图像空间位于同一条直线上的两个不同的点,则根据式(4.65)可以得到如下两式:
yi=pxi+q (4.67)
yj=pxj+q (4.68)
它们在(p,q)上对应的表达式分别为
q=-xip+yi (4.69)
q=-xjp+yj (4.70)
在(p,q)空间里,式(4.69)和式(4.70)表示两条不同的直线。假设它们相交于点(p′,q′),则点(p′,q′)对应了图像空间里的一条通过点(xi,yi)和(xj,yj)的直线。同理,图像空间中过点(xi,yi)和(xj,yj)的直线上的每个点,都对应参数空间中的一条直线。这些直线族在(p,q)空间里均相交于点(p′,q′)。这样,通过计算参数空间中多条直线的交点就可以检测出图像空间中式(4.65)表示的直线。
总之,图像空间中共线的点对应于参数空间相交的线,反之参数空间中相交于同一点的所有直线在图像空间里都有共线的点与之对应。这就是Hough变换中的点-线对偶关系。图4.30给出了一个Hough变换的点、线的图像空间与参数空间对应关系示例。其中,图4.30a所示为图像空间中的直线及其三个点,图4.30b所示为参数空间中分别与三个点对应的直线及其交点。其中,(x,y)空间里的点A对应着参数空间中的直线LA,点B对应着参数空间中的直线LB,点C对应着参数空间中的直线LC。(p,q)空间里的点P0对应着(x,y)空间里的直线L0。

图4.30 图像空间与参数空间的对应关系示例
当被检测的直线为垂直线时,p的取值可以为无穷大。为了避免垂直直线检测时出现问题,通常在参数空间采用极坐标系的形式来表示直线,即
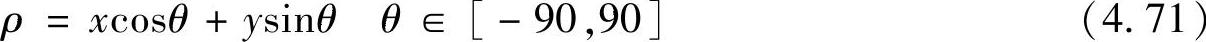 (www.chuimin.cn)
(www.chuimin.cn)
这样,图像坐标系中的一个点(x,y)可以转变成参数空间(ρ,θ)内的一条正弦曲线。此时,Hough变换中的点与直线之间的对偶性就转变成点与正弦曲线之间的对偶变换。
可以证明,直角坐标空间中共线的点经过Hough变换后,它们的正弦曲线在极坐标空间中有一个公共交点。也就是说,参数空间上的一点(θ,ρ),对应于直角坐标O—XY中的一条直线,而且它们是一一对应的。
为了检测出图像坐标系中的直线,可以将参数坐标空间中的θ和ρ进行量化,如图4.31b所示。根据直角坐标中每个点的坐标(x,y),在θ的取值范围内计算各个ρ值。若ρ值落在某个量化小格内,便使该小格的累加计数器加1。当直角坐标中全部的点都变换后,对小格进行检验,计数值最大的小格,根基最大值所对应的参数值(θ*,ρ*)便可以计算出其在直角坐标中的直线表达式。
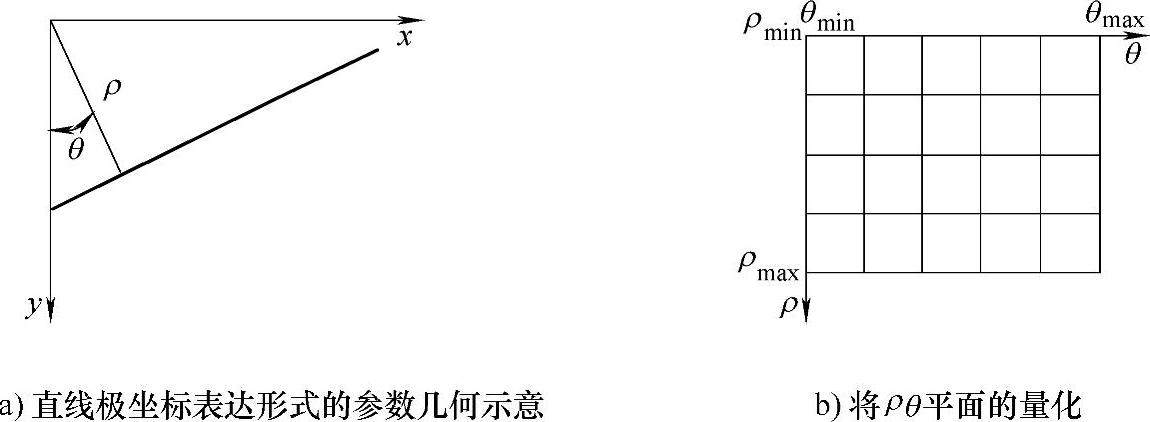
图4.31 Hough变换的直线检测
可见,如果用数组A(θ,ρ)记录量化后的θ及其对应的ρ,那么基于Hough变换的直线检测可以描述为
1)根据精度要求,在ρ和θ的取值范围内对其进行量化,分别将其等分为m和n份,每一等分用ρi和θj表示。
2)自上而下、自左而右遍历图像,如果检测到当前点(x,y)是边缘目标点,则根据式(4.71)算出每一个θj对应的ρi值。
3)根据θj和ρi的值对A进行累加,即
A(θj,ρi)=A(θj,ρi)+1 (4.72)
4)重复执行2)和3),直到所有的目标点都处理完毕。
5)比较数组元素值A(θj,ρi)的大小,找到参数平面上最大值,即找到了与之对应的由式(4.65)所描述的直线,同时也可以知道多少点是共线的。也就是说,直线所对应的极坐标参数为
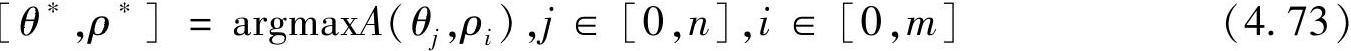
最终检测到的共线直线方程的表达式为

如果检测平面内不止一条直线,那么可以设置一个阈值,如认为A(θj,ρi)的值大于一定的阈值,则认为通过该点的那些曲线所对应的图像空间中的各个点共线;反之如果A(θj,ρi)的值较小,则认为通过该点的那些曲线在图像空间中的对应点均属于孤立点。
需要说明的是,对ρ和θ的量化如果过粗,那么直线参数就不精确;如果量化程度过细,则计算量增加。因此,对ρ和θ的量化要在满足一定精度的精度条件下进行,也要兼顾计算量的问题。示例如图4.32所示。
(2)圆的检测
Hough变换不仅可以检测直线和连接共线点,也可以用来检测圆等其他各类能用解析式表示的曲线。下面再看一下圆的Hough变换。

图4.32 Hough变换直线检测示例
对于图像空间中的一个半径为r、圆心在(a,b)的圆,其直角坐标系方程可以表示为
(x-a)2+(y-b)2=r2 (4.75)
其极坐标表达式为
x=x0+rcosθ (4.76)
y=y0+rsinθ (4.77)
那么在参数空间O-ab里,圆的参数方程为
(a-x)2+(b-y)2=r2 (4.78)其极坐标表达式为
a=x-rcosθ (4.79)
b=y-rsinθ (4.80)
可见,对于参数空间O-ab里的一个圆,在O-xy空间里有一个点(x,y)与之一一对应。在O-xy中所有共圆的点,它们所对应的O-ab空间中的圆都相交于一点,这点就是这些在O-xy空间中共圆点的圆心坐标。
从上述分析中可以看出,为了求解圆方程中的三个参数,必须建立一个三维网格和三维阵列,对于O-xy空间中的一点,对应于O-ab空间中的一个三维二次曲面。若该曲面经过某个小网格,则该网格对应的三维计数单元的值就加1。可见检测共圆点的原理和方法与检测共线点是一致的,只是计算量复杂度增加了。为了便于计算,对式(4.79)进行整理可以得到
a=x-rcosθ⇒r=(x-a)/cosθ (4.81)
因此
b=y-rsinθ⇒b=y-(x-a)sinθ/cosθ⇒b=atanθ-xtanθ+y (4.82)
式中,θ为当前点的梯度角。可见,通过式(4.82)即可得到圆在参数空间上的映射,同时参数由3个变为2个。
根据以上原理,基于Hough变换的圆检测算法的具体步骤如下:
1)根据精度要求,在a和b的取值范围内对其进行量化,分别将其等分为m和n份,每一等分用bi和aj表示。
2)计算原图的梯度、梯度方向及其正切值。
3)自上而下、自左而右遍历图像,如果检测到当前点(x,y)是边缘目标点,查找当前点所对用的梯度角正切值,然后根据式(4.82)算出每一个aj对应的bi值。
4)根据aj和bi的值对计数累加器A进行累加,即
A(aj,bi)=A(aj,bi)+1 (4.83)
5)按照式(4.82)获得参数空间上的直线,对直线上的点累计加1。
6)循环3)和5),直到所有的点全部处理完毕。
7)在参数空间上找到累计值为最大的点,即找到了与之对应的、由式(4.82)描述的圆心。
8)获得圆心坐标之后,代入图像空间中圆的式(4.75),即可获得圆的半径。
梯度角及其正切值的计算是曲线检测中的基础,下面给出一种计算方法。
计算梯度时,可采用图4.33所示的模板。首先用中心像素与其周围的8个像素分别求差分,然后取绝对值为最大的一点为当前点的梯度值。当最大值处于1或5的位置,tanθ=-1;当最大值处于2或6的位置,tanθ=0;当最大值处于3或7的位置,tanθ=1;当最大值处于4或8的位置,tanθ=∞。由于图像中去掉若干个点不影响对圆的检测,因此若最大值处于4或8的位置上时,其梯度值及其角度的正切值同时置为0,表明该点不参与运算。

图4.33 梯度模 板示意图
除了能检测圆(见图4.34)等能用解析形式表达的曲线外,Hough变换还能够检测那些复杂的、难以用解析式表达的曲线,相关内容可以查阅广义Hough变换的相关内容。
4.曲线拟合
如果已确定的边缘点很稀疏,可以通过它们用直线段或样条函数拟合来获取边界段并进而得到完整的边界。
(1)迭代终点拟合法
如图4.35所示,设在边缘点A和B之间有一些已检测出的散布边缘点,希望通过它们中的一些点用若干直线段把A和B连接起来。为此,首先可用一直线连接A和B,然后计算从各个散布边缘点到这条直线的垂直距离。将对应距离最大的点C当作A和B间边界中的一个点,它有分别连接点A和点B的两个分支。对这两个分支每个分支重复上述过程,直到没有边缘点到已建立的直线段集合的距离大于某个预先确定的距离为止。图4.42c所示是考虑点D的两个分支,设点F和点G与对应线段的距离均小于预先确定的允许距离,不许进一步考虑,所以线段ABCD构成点A和点B间的近似边界。如果将上述过程绕目标一周即可得到多变形边界,类似于采用分裂方法逼近多变形边界技术。

图4.34 Hough变换圆检测示例
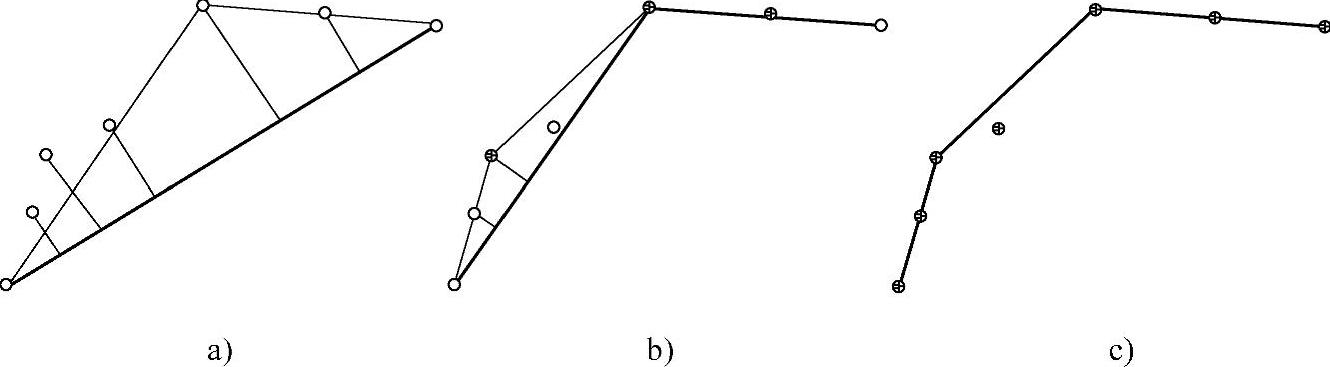
图4.35 迭代终点拟合示例
(2)最小方均误差曲线拟合
给定一组边缘点{(xi,yi),i=1,2,…,N},一种常用的曲线拟合方法是找到一个函数f(x)以最小化下列误差,即

如果f(x)是一条抛物线,它的方程可表示为

则拟合就是要确定式(4.85)中的各个系数。下面借助矩阵来推导一种解法,设

则误差列矩阵为
E=Y-MC (4.87)
这样方均误差是

对C的各个元素求导,并取导数为零可解得

C中的元素给出最小方均误差的拟合系数。如果边界点数与拟合系数个数相同,M是一个方阵,则可以直接求逆
C=M-1Y (4.90)
有关视觉测量技术的文章

最常见的成像变换是几何透视变换,其特点是随着三维场景与摄像机之间距离的变化,像平面上的投影也发生变化。假设摄像机理想成像,不存在非线性畸变,如图5.6所示。针孔模型主要由光心、成像面和光轴组成。图5.6 小孔成像模型......
2023-11-24

单目视觉测量是指利用一台摄像机或数码相机拍摄图像进行测量工作。但由于标定精度弱和难以同时确定摄像机与被测物体之间的相对位置等问题,单目视觉的整体测量精度不如双目和多目视觉测量系统。单目视觉测量的理论基础和相关技术是双目测量乃至多目测量技术的基础。单目视觉测量能够满足某些应用场合实际测量的要求。基于单目视觉的测量方法主要包括几何相似法、光笔式三坐标测量法、几何形状约束法、几何光学法和结构光测量等。......
2023-11-24

借鉴人类视觉的原理,计算机视觉技术研究的长远目标是建立通用的视觉系统。计算机视觉技术的优势不仅在于能模拟人眼的功能,还能完成人眼所不能胜任的工作。因此,对人脑视觉的充分理解将促进对计算机视觉更深入的研究,并对计算机视觉系统提供坚实的生物理论基础。......
2023-11-24

图4.10 边缘模型边缘检测是基于边界分割方法的最基本处理。实际边缘模型是如图4.10b所示的水平剖面图,称为斜坡边缘。斜坡部分与边缘的模糊程度成比例。阶跃型边缘处于图像中两个具有不同灰度值的相邻区域之间,其灰度变化曲线的一阶导数在边缘处出现极值,而二阶导数在边缘处出现零交叉。脉冲型边缘主要对应于细条状的灰度值突变区域。边缘检测包含两个方面含义:1)检测边缘点或边缘线段。......
2023-11-24

如图7.17所示,设P是空间中的一个物点,O和O′分别是左、右摄像机的光学中心。由几何知识可知,以P、O和O′三点为顶点可以构成一个三角形,它们确定空间中的一个平面π。由于处于空间中同一个平面上的两条非平行直线惟一地确定平面上的一点,因此物点P由上述两直线OPLi和O′PRi的交点给出。因此,必须通过必要的信息或约束规则作为辅助判据,以便得到惟一准确的匹配。图7.17 双目视觉系统的基本几何约束......
2023-11-24

计算机视觉测量技术以图像传感器为手段检测空间物体的空间三维坐标,进而检测物体的尺寸、形状和运动状态等。美国、加拿大、日本等发达国家早在20世纪60年代后期就已经开始了计算机视觉测量技术的研究。直到20世纪90年代,随着计算机技术的发展成熟,计算机视觉测量技术逐渐成为一个研究热点。......
2023-11-24

下面简要介绍Marr视觉理论的基本思想和框架。图1.1 Marr视觉信息处理的三个阶段第一阶段是早期视觉处理,其目的是从输入的原始图像中抽取观察者周围景物表面的物理特性,如距离、表面方向、材料特性等,并构成要素图或基元图。表1.2 由图像恢复形状信息的表达框架3.Marr视觉理论的意义及不足Marr视觉理论是计算机视觉研究领域的划时代成就。图1.2 改进后的Marr视觉理论框架限于历史等因素,Marr没有研究如何用数学方法严格地描述视觉信息的问题。......
2023-11-24
相关推荐